Abstract
Fractional order Proportional-Integral-Derivative (PID) controller is composed of a number of integer order PID controllers. It is more accurate to control the complex system than the traditional integer order PID controller. The values of parameters of the fractional order PID controller play a decisive role for the control effect. Because the fractional order PID controller added two adjustable parameters than the traditional PID controller, it is very difficult to tune parameters. So the Back Propagation (BP) neural network is selected to optimize the parameters of the fractional order PID controller in order to obtain the high performance. Then the optimized fractional order PID controller and the traditional PID controller are used to control AC motor speed governing system. And the vibration spectrum and stator current spectrum under different rotating speeds are compared and analyzed in detail. The results show that the optimized fractional order PID controller has better vibration suppression performance than the traditional PID controller. The reason is that the optimized fractional order PID controller changed the stator current component, and further changed the frequency components and the amplitude of the vibration signal of the motor.
1. Introduction
In the vast mechanical devices and system dynamics, the vibration is inevitable. It can be seen in the engineering and daily life [1]. It will cause noise and reduce the equipment accuracy and reliability. Motor is regarded as typical rotating machinery, its vibration mainly includes the electromagnetic vibration and mechanical vibration [2-4]. Due to the magnetic flux interactions in the air gap of motor, the electromagnetic vibration generates the radial force wave with time and space variation, which make the vibration of stator core and frame to cause the ambient air pulsation to occur the airborne noise. The mechanical vibration is caused by the mechanical unbalance of rotor and the bearing. The vibration of motor will generate the damages [5], including bending and fracture of motor rotor, rotor pole loosening for causing the mutual collision between stator and rotor, acceleration of motor bearing wear for shortening bearing of the normal life, motor tie line loosing for causing the friction between the end windings and insulation breakdown, and so on. So the vibration suppression of motor has been an important problem. Vibration suppression is an important branch in the field of control engineering, and it is the starting point and the end result of vibration research.
Fractional calculus is an extended form of integer order calculus. It is gradual changing process of the integral or differential [6]. In this sense, the integer order calculus is only a special case of fractional calculus when the differential or integral is an integer. With the rapid development of modern computer hardware, software, and computational intelligence, the fractional calculus theory is applied in many areas in recent years. The fractional is introduced into the controller to increase the integral and differential order for obtaining more flexible control form and better control effect. Because the fractional calculus has some characteristics, the fractional order automatic control theory is gradually heating up in recent years. The fractional order PID controller is one used form of fractional order controllers. But in the actual engineering applications, the parameters of fractional order PID controller are critical to performance of fractional order PID controller. So there are a lot of researches to study optimizing parameters of fractional order PID controller. Wang et al. [7] proposed a new discretization scheme for the design of a fractional order PID controller. Arijit et al. [8] proposed the differential evolution (DE) algorithm to design fractional-order proportional-integral-derivative (FOPID) controllers involving fractional-order integrator and fractional-order differentiator. Wang et al. [9] proposed the concept of fractional-order difference feedback that generalizes the displacement difference feedback, velocity difference feedback and acceleration difference feedback for improving the stability of a soft vibration system. Lee et al. [10] proposed an improved EM algorithm with genetic algorithm technique(IEMGA) for optimizing the fractional-order PID(FOPID) controller based on the electromagnetism-like algorithm. Fabrizio et al. [11] proposed a set of tuning rules for standard (integer-order) PID and fractional-order PID controllers. Saptarshi et al. [12] proposed a novel fractional order(FO) fuzzy Proportional-Integral-Derivative (PID) controller, which works on the closed loop error and its fractional derivative as the input and has a fractional integrator in its output. Tang et al. [13] proposed the design of FOPID controller by using chaotic ant swarm(CAS) optimization method. Saptarshi et al. [14] proposed the improved discrete PID controller based on the continuous and discrete time Linear Quadratic Regulator (LQR) theory and Genetic Algorithm (GA). Wang et al. [15] proposed a graphical tuning method for fractional-order PID controllers based on the sensitivity function constraint of the closed-loop, which provides the information on robustness to plant uncertainties. Wang et al. [16] proposed an efficient way to tune fractional order fuzzy PID controller parameters by using a fruit fly optimization algorithm (FOA), which treats the controller parameters tuning as an optimization problem with a proper fitness function. Alagoz et al. [17] proposed a stochastic, multi-parameter, divergence optimization method for the auto-tuning of proportional-integral-derivative (PID) controllers according to a fractional-order reference model. Yeroglu et al. [18] proposed a stochastic multi-parameters divergence method for online parameter optimization of fractional-order proportional-integral- derivative (PID) controllers. Sudalaiandi et al. [19] proposed an automatic tuning of multivariable Fractional-Order Proportional, Integral and Derivative controller(FO-PID) parameters using Covariance Matrix Adaptation Evolution Strategy (CMAES) algorithm. Padula et al. [20] proposed a fractional-order proportional-integral-derivative controller design based on the solution of an H model matching problem for fractional first-order-plus-dead-time processes. Cheon et al. [21] proposed a new model reduction method and an explicit PID tuning rule for the purpose of PID auto-tuning on the basis of a fractional order plus time delay model. Mishra et al. [22] proposed an attempt to propose an intelligent control system which takes the form of a fractional order fuzzy proportional-integral-derivative (FOFPID) controller which is investigated as a solution to deal with the complex dynamic nature of the distillation column. Indranil et al. [23] proposed the gains and the fractional differ-integral orders of the FOPID controllers in the two areas. Saidi et al. [24] proposed a robust fractional order PID controller design based on numerical optimization. Zhong et al. [25] proposed the design of a fractional-order (FO) PID controller and its application to stabilizing an FO solid-core magnetic bearing (MB) system. Mousavi et al. [26] proposed a novel memetic algorithm namely Fractional Particle Swarm Optimization-based Memetic Algorithm (FPSOMA) to solve optimization problem using fractional calculus concept. Mohanty et al. [27] proposed the application of fractional order PID controller (FOPID) for reactive power compensation and stability analysis.
Vibration suppression is to meet the requirements of the vibration level for the controlled object by using certain methods. For vibration suppression problem, many researchers proposed a variety of vibration control strategies and methods. Mohamed et al. [28] proposed a non-collocated proportional-integral-derivative (PID) controller based on input shaping techniques for vibration suppression. Li et al. [29] proposed an integration of a fractional-order disturbance observer and a single neuron-based PI fuzzy controller for vibration suppression. Cychowski et al. [30] proposed the model predictive control (MPC) for high-performance speed control and torsional vibration suppression. Onat et al. [31] proposed a fractional controller for the suppression of the flexural vibrations of the first mode of a smart beam. Aghababa [32] proposed a novel fractional-order sliding mode control to attenuate the vibrations of structures with uncertainties and disturbances. Lu et al. [33] proposed a novel control strategy for vibration suppression using an integration of a fractional-order disturbance observer (FDOB) and an adaptive grey predictive controller (AGPC). Sun et al. [34] proposed two-parameter fractional-order model of viscoelastic material to derive the fractional-order dynamics of rigid-flexible coupling structures to simplify the modeling and controller design for residual vibration suppression. Zhang et al. [35] proposed the Disturbance Rejection (DR) control for vibration suppression of smart structures under high frequency periodic disturbances.
At present, the vibration suppression methods of motor are eliminated or reduced by improving the structure, material and increasing damping device and so on. The implementation complexity of the system is increased on the extent. At the same time, it is significant to study the vibration suppression problem from the perspective of control strategy. At present, the less researchers use the fractional order control strategy to study the vibration suppression problem, and achieved certain suppression effect. But the performance of the fractional order controller is mainly determined by the optimization of the relevant parameters. So the back propagation (BP) neural network is selected to optimize the parameters of fractional order PID controller in order to avoid the uncertainty and complexity of the manual adjusting parameters of fractional order PID controller in this paper. The optimized outputs of BP neural network are used as the parameters of fractional order PID controller in order to obtain an optimized fractional order PID controller, which is used to suppress vibration of AC motor in speed control system. And the vibration frequency spectrum in different frequency band are compared by using the optimized fractional order PID controller and traditional PID controller for controlling 15 KW motor in order to testify effectiveness of vibration suppression performance.
2. Fractional order PID controller
Up to now, the fractional calculus theory has been in existence for more than 300 years, and the fractional order calculus is a relatively complicated calculation and analysis method. In essence, there is a big difference between the fractional calculus and the integer order calculus. The fractional calculus has a remarkable memory, but the integer order calculus has not the memory function [36]. The fractional calculus is not only related to the current time, but also to the past time, and the integral calculus is only related to the current time.
Fractional order PID controller is an extension of the traditional PID controller, its foundation is the fractional calculus. For the fractional order PID controller, because the transfer function involves the accumulation of time step, it can obtain good control effect for the time-varying in industrial production. These advantages do not have in the traditional PID controller. For the controlled system with fractional order PID controller, the basic principle structure is shown in Fig. 1.
The closed-loop control system is composed of the fractional order PID controller and the feedback control system of the controlled object model. The given input value and actual output value are used to execute the algebraic operation to obtain error , which is regarded as the input of the fractional order PID controller. Then the output of the fractional order PID controller is obtained by operating the proportion, fractional order differential and integral. The is added to the plant input of the controlled object model in order to control the controlled object and ultimately achieve the desired output. The computation expression of the fractional order PID controller in time domain is described as follow:
Fig. 1The principle structure of the fractional order PID controller
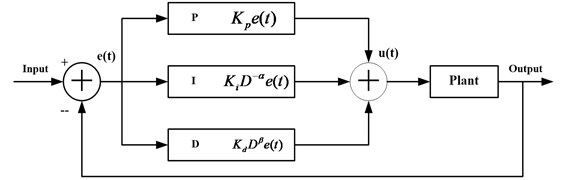
The fractional order PID controller is developed based on the fractional order theory. The fractional differential and integral can be expressed by using and . is the differential order, is the integral order, the subscript and are the upper and lower bounds. It has been widely acknowledged that the definition of fractional calculus has two kinds: Grünwald-Letnikov fractional order calculus and Riemann-Liouville fractional order calculus [37].
Riemann-Liouville fractional order calculus is defined as follow:
where , is Gamma function, . Under the zero initial condition, the transform of Laplace is obtained:
Grunwald-Letnikov fractional order calculus is defined as follow:
where .
When the function has a ( 1) – order continuous derivative, the definitions of the Grunwald-Letnikov and Riemann-Liouville are completely equivalent.
In order to apply the fractional order calculus, the digital realization algorithms of the fractional order calculus are proposed in recent years.
In this paper, a rational approximation method of fractional calculus operator () based on the best rational approximation definition in the given frequency range and the error is introduced [38, 39]. A design method of a fractional order PID controller based on the above rational approximation method of fractional calculus operators is implemented here.
The discussed approximation is a subset of rational functions on [, ], and it is the best approximation of a given irrational function under the normal . For fractional calculus operators , the best rational approximation function definition for can be given as follows.
Definition 1. Let function , ; for any point in the frequency range , is the amplitude of the rational approximation function at point and is the amplitude of at point . The best approximation function of in can be defined as:
where , and is a rational function set.
is called the maximum amplitude error between and If the function is , then:
then is called the best rational approximation function of .
In Definition 1, the notation means a rational function, which is expressed in the following general form:
is a set, which is composed of ; is called a rational function class.
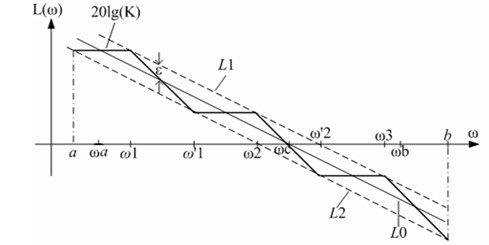
The construction method of the fractional order integral operator is shown in Fig. 2.
The [, ] is the approximation range and the [] is interested approximation band. To improve the approximation accuracy, the [, ] contains the [].
The fractional order integral operator is represented by L0. The (dB) is the maximum permission error of the amplitude frequency characteristic. The other asymptote line L1 and line L2 are parallel to line L0. The polygonal line for scope 0 dB and –20 dB between line L1 and line L2 is used to represent .
The detailed derivation process see reference [38, 39]. The approximation function of is represented by using the following equation:
where, is the selected first turnover frequency. And , , .
3. The optimized fractional order PID controller based on BP neural network
Fractional order PID controller is a general form of integer order PID controller. Because the integral and differential orders are arbitrary values in the range (0, 1), the fractional order PID controller is more flexible than the integer order PID controller. However, the fractional order PID controller has five adjustable parameters, which makes to adjust the parameters of the fractional order PID controller to become relatively difficult. It is difficult to find suitable parameters of the fractional order PID controller for taking on good control performance. So back propagation (BP) neural network is selected to optimize and select the parameters of the fractional order PID controller in order to improve the control precision.
3.1. Construct BP neural network model
The BP neural network is multilayer feed forward neural network, which is composed of the input layer, hidden layer and output layer. The full connection mode is used among the layers. The neurons cannot be connected in the same layer, and the low level neurons can only transfer information to high-level neurons, reverse transfer for correction error. When the parameters are better set, the BP neural network can converge to a smaller mean square error and successfully realize the multilayer artificial neural network. The structure determining of BP neural network mainly includes the nodes of the input layer, hidden layer and output layer, and coefficient [40]. The input nodes in the input layer are the error and error change rate of the current moment and previous moment. The output nodes in the output layer are determined by adjustable parameters of the fractional order PID controller. The nodes in the hidden layer are as far as possible less and feasible principle. The selected nodes are 5 by referring the previous experiment results in the hidden layer. So the structure of BP neural network is 4-5-5, shown in Fig. 3.
Fig. 2Logarithmic amplitude frequency characteristic curve and the asymptote
The input information respectively contains the error (), error change rate (), previous time error () and previous time error change rate (). The output signals are the proportional coefficient (), integral coefficient (), differential coefficient (), differential index () and integration index ().
The mathematical expressions of the input and output in each layer are given according to the network structure.
1) The expressions of the input layer:
2) The input and output expressions of all nodes in the hidden layer:
The nodes in the hidden layer use Sigmoid transfer function, its expression is:
3) The input and output expressions of all nodes in the output layer:
Fig. 3The structure of BP neural network
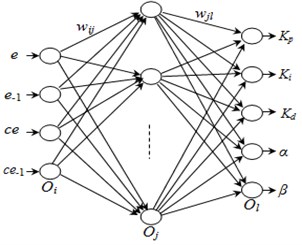
Fig. 4BP neural network-based controller structure
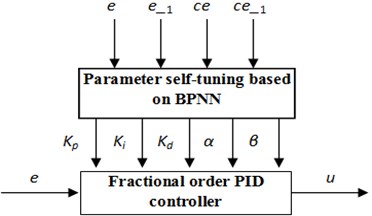
3.2. The optimized fractional order PID controller
If the fractional order PID controller can achieve the desired results, the parameters of the fractional order PID controller need be adjusted at the same time. There exist the relations and constraints among these parameters. So BP neural network is introduced into the fractional order PID controller. The self-learning function of BP neural network is used to automatically adjust the parameters. The tuning parameter method based on BP neural network is shown in Fig. 4.
The steps of the optimizing parameters are described as follows:
Step 1. Initialization. The initial weights of each nervous layer are given, and the learning rate and momentum factor are selected.
Step 2. The given system input is , and the actual system output is , the error is -.
Step 3. Calculate the input and output of the neural network in each layer.
Step 4. Calculate the output of the fractional order PID controller.
Step 5. The gradient descent method is used to adjust the weight coefficient of BP neural network. When the error is in the range of requirements, the adjustment is stopped to obtain the optimal combination values of parameters of BP neural network.
Step 6. The optimized BP neural network is used to optimize and select the , , , and of the fractional order PID controller in order to realize the self-adaptive parameters.
Step 7. Set , return to Step 2 until the maximum number of iterations is reached.
3.3. Simulation results and analysis
In order to verify the performance of the self-tuning algorithm of the fractional order PID controller, the validity of the self-tuning algorithm verified on the Matlab platform. First, each variable is initialized for the algorithm in order to the output of the control system. The difference between system output value and system given value is obtained, which is regarded as the system error. When the system error is greater than the threshold, the BP neural network is used to optimize and select the parameters of the fractional order PID controller. When the system error is less than the threshold, the values of parameters will enter into the fractional order PID controller to control the whole system.
The tuning process of parameters of the optimized fractional order PID controller is shown in Fig. 5.
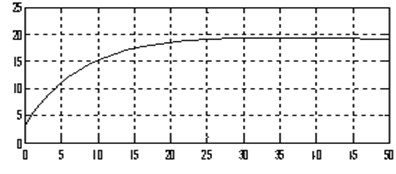
The output curve of the optimized fractional order PID controller is shown in Fig. 6.
Fig. 5 is the change curve of five parameters (, , , and ) of the optimized fractional order PID controller. Fig. 6 is the output curve of the optimized fractional order PID controller. As it can be seen from the Fig. 5 and Fig. 6, the optimized fractional order PID controller reaches stable state in the short time. After the parameters reach the stable state, the control system does not appear the oscillation phenomena. The effectiveness of the neural network is verified to tune parameters of fractional order PID controller.
Fig. 5The tuning process of parameters of the fractional order PID controller
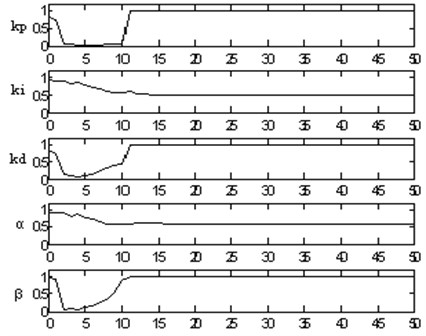
Fig. 6The output curve of the optimized fractional order PID controller
4. Analysis of stator current spectrum and vibration spectrum
4.1. Experiment system
In order to collect the experiment data, 15 kW AC motor is selected to test the effectiveness of vibration suppression by using the optimized fractional order PID controller. Parameters of motor and inverter are given in Table 1. Data collection is conducted under the following conditions: the sampling frequency is 25600 Hz, 15 kW AC motor run steadily at different speeds (450 r/min, 600 r/min, 750 r/min, 900 r/min). Four vibration acceleration sensors collect four road vibration data from four different positions on the motor. Their positions and parameters are respectively given in Fig. 7 and Table 1.
Table 1Parameters of acceleration sensors
NI9234 channel | Voltage sensitivity (mV/g) | Model | Resolution (m/s2) | Velocity range (m/s2) | Constant current (mA) | Frequency response range (Hz) |
AI0 | 97.81 | 14100 | 0.01 | ±500 | 2-10 | 1-8000 |
AI1 | 95.95 | |||||
AI2 | 100.84 | |||||
AI3 | 99.17 | 14105 |
In the Fig. 7, the label is named by using the channel number of NI9234. The locations of four vibration acceleration sensors include the radial vertical direction, radial horizontal direction of motor bearing, motor base and the radial vertical direction of generator bearing. In four positions, it is important to study the vibration of the radial vertical direction of motor bearing. So the vibration of the radial vertical direction is only selected in this paper. When the stator current signal is required, the AI3 channel will be used to acquire the current signal.
Fig. 7Positions of acceleration sensors

4.2. Spectrum analysis by using the optimized fractional order PID controller
In order to verify the vibration suppression effectiveness of the optimal fractional order PID controller, the 15 kW AC motor is used as the research object, and the traditional PID controller is used to compare with the optimal fractional order PID controller. The low frequency band, high frequency band and the carrier wave frequency spectrums by using the optimal fractional order PID controller and traditional PID controller are compared in order to analyze the performance influence of the vibration suppression for the motor.
4.2.1. Study the relationship between vibration and current
The vibration spectrum and stator current spectrum of 15 kW AC motor with 600 r/min is shown in Fig. 8.
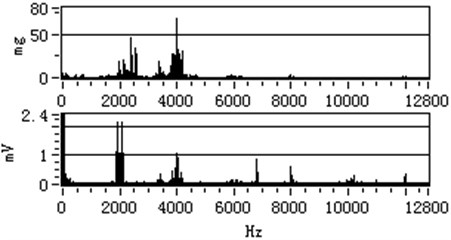
The vibration spectrum and stator current spectrum of 15 kW AC motor with 900 r/min is shown in Fig. 9.
Fig. 8The vibration spectrum and stator current spectrum with 600 r/min
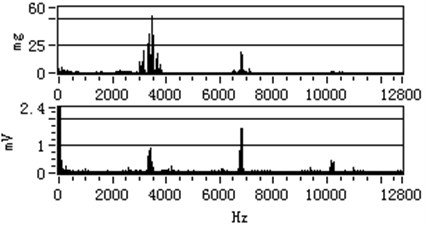
In the Fig. 8 and Fig. 9, the above part is vibration spectrum and the below part is stator current spectrum. Because the stator current is collected by the sampling resistance, the voltage unit is used. By comparing the vibration spectrum and stator current spectrum under different speeds, it can discover that their spectrums have similar characteristics. The vibration frequency spectrum and stator current frequency spectrum of motor have similar characteristics under the other rotating speeds, so they are not described in here.
Fig. 9The vibration spectrum and stator current spectrum with 900 r/min
4.2.2. Compare and analyze the spectrum of low frequency band
In order to prove the suppression effect of the optimal fractional order PID controller, the obtained vibration acceleration data and stator current data are analyzed.
The comparison results of vibration spectrum and current spectrum in [0 Hz, 100 Hz] under the optimal fractional order PID controller and the traditional PID controller is shown in Fig. 10.
In the Fig. 10, is he vibration spectrum and is the stator current spectrum under each relating speed. As it can be seen from the Fig. 10, it is obvious that the peak amplitude of the same frequency and the frequency doubling of the current spectrum under the optimal fractional order PID controller is lower than that under the traditional PID controller. And vibration spectrum near 30 Hz, 55 Hz and 70 Hz are obvious peak. The peak value will increase with increasing rotating speed.
Fig. 10The comparison result of vibration spectrum in [0 Hz, 100 Hz]
![The comparison result of vibration spectrum in [0 Hz, 100 Hz]](https://static-01.extrica.com/articles/16652/16652-img10.jpg)
a) PID controller
![The comparison result of vibration spectrum in [0 Hz, 100 Hz]](https://static-01.extrica.com/articles/16652/16652-img11.jpg)
b) Optimed controller
In order to illustrate the vibration suppression effectiveness of the optimized fractional order PID controller, the concept of suppression ratio is introduced to describe the relationship of spectrum peak amplitude. The peak amplitudes of vibration and current frequency spectrum at one frequency point of integer order PID controller and fractional order PID controller are and respectively, and the peak suppression ratio PVS is defined as follow:
where PVS is the vibration and current suppression ratio.
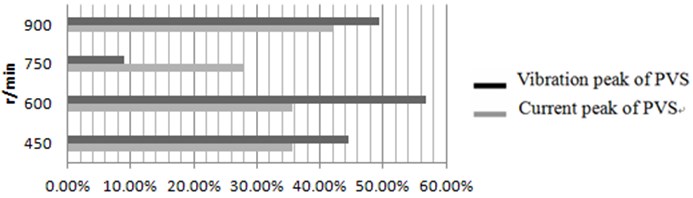
The suppression ratio of largest current spectrum peak under all speeds is show in Table 2.
The result of peak suppression ratio of current and vibration in low frequency band is show in Fig. 11.
From the analysis results, we can know that the optimal fractional order PID controller has better vibration suppression performance than the traditional PID controller in [0 Hz, 100 Hz].
Table 2Current PVS in [0 Hz, 100 Hz]
Rotating speed (r/min) | Peak frequency (Hz) | Peak amplitude of PID (mV) | Peak amplitude of (mV) | PVS | The average of peak suppression ratio |
450 | 15 | 0.36 | 0.2 | 44.44 % | 39.86 % |
600 | 19 | 0.44 | 0.19 | 56.82 % | |
750 | 25 | 0.45 | 0.41 | 8.89 % | |
900 | 29 | 1.44 | 0.37 | 49.31 % |
Fig. 11The result of peak suppression ratio of current and vibration in low frequency band
4.2.3. Compare and analyze the spectrum of high frequency band
The comparison result of vibration spectrum in [100 Hz, 1700 Hz] under the optimal fractional order PID controller and the traditional PID controller is shown in Fig. 12.
As it can be seen from the Fig. 12, it is obvious that the optimized fractional order PID controller has better vibration suppression effect for motor, especially the vibration peak in the frequency of 192 Hz, 440 Hz, 620 Hz and 700 Hz. The vibration peak of this frequency band is effected by mechanical vibration characteristic of the motor.
4.2.4. Compare and analyze the spectrum of carrier wave band
The comparison result of no-load vibration and current data with 600 r/min under the optimal fractional order PID controller and the traditional PID controller is shown in Fig. 13. In here, the carrier frequency is 3.4 kHz.
As it can be seen from stator current spectrum and vibration spectrum in the Fig. 13, it is obvious that the spectrum peak under the optimized fractional order PID controller is smaller than the spectrum peak under the traditional PID controller at carrier frequency and frequency doubling. The result show that the optimized fractional order PID controller can better suppress the vibration caused by converter carrier wave frequency.
Fig. 12The comparison result of vibration spectrum in [100 Hz, 1700 Hz]
![The comparison result of vibration spectrum in [100 Hz, 1700 Hz]](https://static-01.extrica.com/articles/16652/16652-img13.jpg)
a) PID controller
![The comparison result of vibration spectrum in [100 Hz, 1700 Hz]](https://static-01.extrica.com/articles/16652/16652-img14.jpg)
b) Optimed controller
Fig. 13The comparison result of no-load vibration and current data with 600 r/min
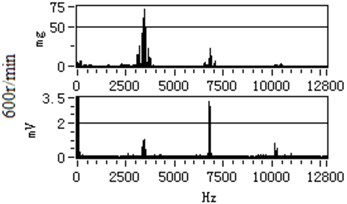
a) PID controller
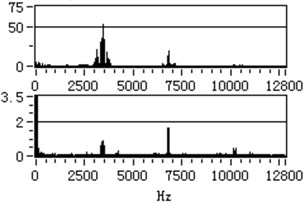
b) Optimed controller
In order to further study the influence of converter carrier frequency to the vibration, the carrier frequencies of converter are respectively set 3.4 kHz and 6.8 kHz. The stable operation spectrum data under 450 r/min, 600 r/min and 750 r/min are compared and analyzed in Table 3.
Table 3The vibration and current suppression ratio under different speed
Data type | Speed r/min | PID controller | Fractional order PID controller | PVS | |||
3.4 kHz spectrum peak value | 6.8 kHz spectrum peak value | 3.4 kHz spectrum peak value | 6.8 kHz spectrum peak value | 3.4 kHz | 6.8 kHz | ||
Vibration frequency spectrum (mg) | 450 | 63.63 | 25.54 | 36.61 | 14.72 | 42.46 % | 42.36 % |
600 | 72.98 | 22.63 | 52.44 | 19.39 | 28.14 % | 14.32 % | |
750 | 138.76 | 18.08 | 69.19 | 13.48 | 50.14 % | 25.44 % | |
The average value of suppression ratio | 40.25 % | 27.37 % | |||||
Current frequency spectrum (mV) | 450 | 0.78 | 2.75 | 0.42 | 2.28 | 46.15 % | 17.09 % |
600 | 1.07 | 3.26 | 0.92 | 1.65 | 14.02 % | 49.39 % | |
750 | 2.12 | 2.19 | 1.18 | 1.43 | 44.34 % | 34.70 % | |
The average value of suppression ratio | 34.84 % | 33.73 % | |||||
As can be seen from Table 3, the vibration suppression performance of the fractional order PID controller has certain advantages than that of the integer order PID controller.
4.3. Analyze the vibration suppression performance
In order to further analyze the reason why the optimized fractional order PID controller has better effect to the vibration suppression of AC motor, the frequency spectrum of the stator current near the rotating frequency of AC motor is amplified. The amplified frequency spectrum is shown in Fig. 14.
As can be seen from Fig. 14, the optimized fractional order PID controller has better vibration suppression performance because it changes the single-point control into multi-point control of the traditional integer order PID controller. Because the stator current increases the frequency component near the rotating frequency, the generated electromagnetic torque is more stable. This also verifies that the fractional order PID controller is composed of multiple integer order PID controllers.
Fig. 14The amplified frequency spectrum
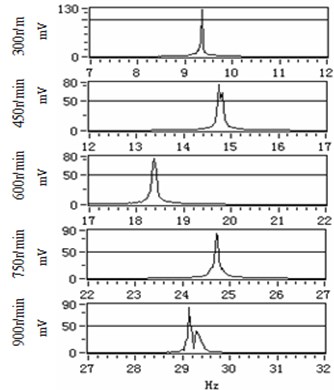
a) PID controller
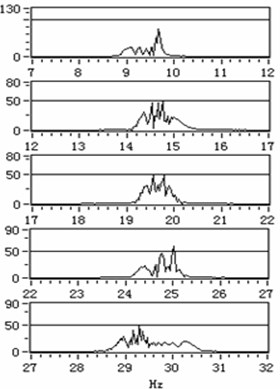
b) Optimed controller
5. Conclusions
With the research and development of fractional calculus theory, the fractional order controller has become a new hot spot in the control research field in recent years. For many complex practical systems, the fractional order controller can achieve better control performance than the integer order controller. The fractional order PID controller is one of the most commonly used fractional order controller. Because it has more than two parameters than the integer order PID controller, which makes that it is difficult to tune the parameters of the fractional order PID controller. So the BP neural network optimization algorithm is used to tune the parameters of the fractional order PID controller in AC motor speed control system in this paper in order to obtain the high performance of the optimized fractional order PID controller. The vibration suppression effect of 15 kW AC motor under the fractional order PID controller and the traditional PID controller is compared and analyzed in detail. The vibration spectrum and stator current spectrum of AC motor under different rotating speeds are compared and analyzed, it is known that the optimized fractional order PID controller has better vibration suppression performance than the traditional PID controller. As is known to all, the motor vibration and electromagnetic torque has a direct relationship, and the electromagnetic torque and stator current of AC motor is proportional. The stator current spectrum near the current rotating frequency is analyzed in detail, it is known that the fractional order PID controller has better vibration suppression performance because it changes the frequency component of the stator current, and then changes the frequency components and the amplitude of the vibration signal of the motor.
References
-
Li Z. J., Cai G. W., Huang Q. B., Liu S. Q. Analysis of nonlinear vibration of a motor-linkage mechanism system with composite links. Journal of Sound and Vibration, Vol. 311, Issues 3-5, 2008, p. 924-940.
-
Toha S. F., Tokhi M. O. PID and inverse-model-based control of a twin rotor system. Robotica, Vol. 29, Issue 6, 2011, p. 929-938.
-
Cernetic J. The use of noise and vibration signals for detecting cavitation in kinetic pumps. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 223, Issue 7, 2009, p. 1645-1655.
-
Kim B. S., Kim M. G., Lee S. H., Lee M. G. Design of a vibration-isolated cushion to reduce the noise and vibration of a hydraulic breaker. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, Vol. 224, Issue 1, 2010, p. 1-9.
-
Charley J., Bodovillé G., Degallaix G. Analysis of braking noise and vibration measurements by time-frequency approaches. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 215, Issue 12, 2001, p. 1381-1400.
-
Mohamed W., Manar A. E., Shawki A. A. Application of an adaptive neuro fuzzy inference system for low speed planetary gearbox vibration control. Low Frequency Noise, Vibration and Active Control, Vol. 34, Issue 3, 2015, p. 323-342.
-
Wang Z. B., Wang Z. L., Cao G. Y., Zhu X. J. Digital implementation of fractional order PID controller and its application. Journal of Systems Engineering and Electronics, Vol. 16, Issue 1, 2005, p. 116-122.
-
Arijit B., Swagatam D., Ajith A., Sambarta D. Design of fractional-order PID controllers with an improved differential evolution. Engineering Applications of Artificial Intelligence, Vol. 22, Issue 2, 2009, p. 343-350.
-
Wang Z. H., Zheng Y. G. The optimal form of the fractional-order difference feedbacks in enhancing the stability of a sDOF vibration system. Journal of Sound and Vibration, Vol. 326, Issues 3-5, 2009, p. 476-488.
-
Lee C. H., Chang F. K. Fractional-order PID controller optimization via improved electromagnetism-like algorithm. Expert Systems with Applications, Vol. 37, Issue 12, 2010, p. 8871-8878.
-
Fabrizio P., Antonio V. Tuning rules for optimal PID and fractional-order PID controllers. Journal of Process Control, Vol. 21, Issue 1, 2011, p. 69-81.
-
Saptarshi D., Indranil P., Shantanu D., Amitava G. A novel fractional order fuzzy PID controller and its optimal time domain tuning based on integral performance indices. Engineering Applications of Artificial Intelligence, Vol. 25, Issue 2, 2012, p. 430-442.
-
Tang Y. G., Cui M. Y., Hua C. C., Li L. X., Yang Y. X. Optimum design of fractional order PIλDμ controller for AVR system using chaotic ant swarm. Expert Systems with Applications, Vol. 39, Issue 8, 2012, p. 6887-6896.
-
Saptarshi D., Indranil P., Kaushik H., Shantanu D., Amitava G. LQR based improved discrete PID controller design via optimum selection of weighting matrices using fractional order integral performance index. Applied Mathematical Modelling, Vol. 37, Issue 6, 2013, p. 4253-4268.
-
Wang D. J., Li W., Guo M. L. Tuning of fractional order PID controllers based on sensitivity constraint. Journal of Process Control, Vol. 23, Issue 6, 2013, p. 861-867.
-
Wang S., Yan B. Fruit fly optimization algorithm based fractional order fuzzy-PID controller for electronic throttle. Nonlinear Dynamics, Vol. 73, Issues 1-2, 2013, p. 611-619.
-
Alagoz B. B., Ates A., Yeroglu C. Auto-tuning of PID controller according to fractional-order reference model approximation for DC rotor control. Mechatronics, Vol. 23, Issue 7, 2013, p. 789-797.
-
Yeroglu C., Ates A. A stochastic multi-parameters divergence method for online auto-tuning of fractional order PID controllers. Journal of the Franklin Institute, Vol. 351, Issue 5, 2014, p. 2411-2419.
-
Sudalaiandi S., Subramanian B. Design of multivariable fractional order PID controller using covariance matrix adaptation evolution strategy. Archives of Control Sciences, Vol. 24, Issue 4, 2014, p. 235-251.
-
Padula F., Vilanova R., Visioli A. Hoptimization-based fractional-order PID controllers design. International Journal of Robust and Nonlinear Control, Vol. 24, Issue 17, 2014, p. 3009-3026.
-
Cheon Ryu Y. J. K. H., Sung S. W., Lee J., Lee I. B. PID auto-tuning using new model reduction method and explicit PID tuning rule for a fractional order plus time delay model. Journal of Process Control, Vol. 24, Issue 1, 2014, p. 113-128.
-
Mishra P., Kumar V., Rana K. P. S. A fractional order fuzzy PID controller for binary distillation column control. Expert Systems with Applications, Vol. 42, Issue 22, 2014, p. 8533-8549.
-
Indranil P., Saptarshi D. Fractional-order load-frequency control of interconnected power systems using chaotic multi-objective optimization. Applied Soft Computing Journal, Vol. 29, 2015, p. 328-344.
-
Saidi B., Amairi M., Najar S., Aoun M. Bode shaping-based design methods of a fractional order PID controller for uncertain systems. Nonlinear Dynamics, Vol. 80, Issue 4, 2015, p. 1817-1838.
-
Zhong J. P., Li L. C. Tuning fractional-order PID controllers for a solid-core magnetic bearing system. IEEE Transactions on Control Systems Technology, Vol. 23, Issue 4, 2015, p. 1648-1656.
-
Mousavi Y., Alfi A. A memetic algorithm applied to trajectory control by tuning of fractional order proportional-integral-derivative controllers. Applied Soft Computing Journal, Vol. 36, 2015, p. 599-617.
-
Mohanty A., Viswavandya M., Mohanty S. An optimized FOPID controller for dynamic voltage stability and reactive power management in a stand-alone micro grid. International Journal of Electrical Power and Energy Systems, Vol. 78, 2016, p. 524-536.
-
Mohamed Z., Tokhi M. O. Hybrid control schemes for input tracking and vibration suppression of a flexible manipulator. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, Vol. 217, Issue 1, 2003, p. 23-34.
-
Li W., Hori Y. Vibration suppression using single neuron-based PI fuzzy controller and fractional-order disturbance observer. IEEE Transactions on Industrial Electronics, Vol. 54, Issue 1, 2007, p. 117-126.
-
Cychowski M., Szabat K., Orlowska-Kowalska T. Constrained model predictive control of the drive system with mechanical elasticity. IEEE Transactions on Industrial Electronics, Vol. 56, Issue 6, 2009, p. 1963-1973.
-
Onat C., Sahin M., Yaman Y. Fractional controller design for suppressing smart beam vibrations. Aircraft Engineering and Aerospace Technology, Vol. 84, Issue 4, 2012, p. 203-212.
-
Aghababa M. A fractional-order controller for vibration suppression of uncertain structures. ISA Transactions, Vol. 52, Issue 6, 2013, p. 881-887.
-
Lu J. S., Xie W. D., Zhou H. B., Zhang A. J. Vibration suppression using fractional-order disturbance observer based adaptive grey predictive controller. Journal of Vibroengineering, Vol. 16, Issue 5, 2014, p. 2205-2215.
-
Sun G. H., Zhu Z. H. Fractional-order dynamics and control of rigid-flexible coupling space structure. Journal of Guidance, Control and Dynamics, Vol. 38, Issue 7, 2015, p. 1324-1329.
-
Zhang S. Q., Schmidt R., Müller P. C., Qin X. S. Disturbance rejection control for vibration suppression of smart beams and plates under a high frequency excitation. Journal of Sound and Vibration, Vol. 353, 2015, p. 19-37.
-
Zhao H. M., Nie B., Li W., Deng W. Research on fractional order controller based on best rational approximation approach. Journal of Convergence Information Technology, Vol. 7, Issue 4, 2012, p. 50-58.
-
Meng F. W., Liu C. Y., Li Z. J., Wang L. P. Adaptive PI control strategy for flat permanent magnet linear synchronous motor vibration suppression. Chinese Journal of Mechanical Engineering (English Edition), Vol. 26, Issue 1, 2013, p. 11-20.
-
Li W., Zhao H. M. A method of rational function approximation for fractional order differential and integral operator. Acta Automatica, Vol. 37, Issue 8, 2011, p. 999-1005.
-
Zhao H. M., Nie B., Li W., Deng W. Research on fractional order controller based on best rational approximation approach. Journal of Convergence Information Technology, Vol. 7, Issue 4, 2012, p. 50-58.
-
Wang H. S., Wang Y. N., Wang Y. C. Cost estimation of plastic injection molding parts through integration of PSO and BP neural network. Expert Systems with Applications, Vol. 40, Issue 2, 2013, p. 418-428.
Cited by
About this article
The authors would like to thank all the reviewers for their constructive comments. This research was supported by the National Natural Science Foundation of China (U1433124, 51475065), Open Project Program of State Key Laboratory of Mechanical Transmissions (Chongqing University) (SKLMT-KFKT-201513, SKLMT-KFKT-201416), the Natural Science Foundation of Liaoning Province (2015020013), Open Fund of Key Laboratory of Guangxi High Schools for Complex System and Computational Intelligence (15CI06Y), Open Project Program of Guangxi Key laboratory of hybrid computation and IC design analysis (HCIC201507, HCIC201402), Open Project Program of the Traction Power State Key Laboratory of Southwest Jiaotong University (TPL1403), the Open Project Program of Sichuan Provincial Key Lab of Process Equipment and Control (GK201404). The program for the initialization, study, training, and simulation of the proposed algorithm in this article was written with the tool-box of MATLAB 2010b produced by the MathWorks, Inc.
