Abstract
This paper investigates the free vibration characteristics of truncated conical shells with variable thickness using the Haar wavelet method. Based on the Love first-approximation theory, the governing partial differential equations are formulated, which are transformed into ordinary differential equations using the separation of variables. The Haar wavelet discretization method is introduced to predict the dynamic characteristics of truncated circular conical shells with linearly and parabolically varying thickness. The present analysis is validated by comparing the numerical results with those available in the literature and very good agreement is achieved. The effects of geometrical parameters and boundary conditions on the vibration characteristics of conical shells with variable thickness are presented. The advantages of this method consist in its simplicity, fast convergence and high precision.
1. Introduction
The truncated circular conical shells are widely used as structural elements in various branches of engineering such as mechanical, marine, civil and power engineer. The static and dynamic characteristics of this shell-type of structures have been of great interest to many researchers [1-13]. Irie et al. [1, 2] analyzed free vibration characteristics of conical shells with constant and variable thickness using the transfer matrix method. The free vibration analysis of laminated conical shells with variable thickness was conducted by Sankaranarayanan et al. [3] using the energy method based on the Rayleigh-Ritz procedure. The semi-analytical finite element method was implemented by Sivadas and Ganesan [4] to study the effects of thickness variation on natural frequencies of laminated conical shells. Tong [5, 6] investigated the free vibrations of orthotropic and composite laminated conical shells using the power series expansion approach. The global method of generalized differential quadrature (GDQ) was applied by Shu [7] for the first time to study the free vibration of isotropic conical shells. Lam and Hua [8, 9] employed the Galerkin method to study the influence of boundary conditions on free vibration characteristics of truncated circular isotropic and orthotropic conical shells. Lam and Hua [10] also presented the influence of orthotropic material on frequencies characteristics of thin truncated circular symmetrical cross-ply laminated conical shells using the GDQ method. Omer [11], Liew et al. [12], Jin et al. [13] performed free vibration analysis of conical shells using discrete singular convolution (DSC) method, the element-free kp-Ritz method and the modified Fourier series solution, respectively. The literature clearly shows that there is few investigation on vibration of conical shells with variable thickness. This mainly because that the additional terms due to the variable thickness will make the governing equations more complicated than the uniform shells, and the conventional methods are unable or complex to extend to the problems of this type of structures. Thus, it is necessary to develop an efficient approach to solve the dynamics of this type of structures. The main aim of this present paper is to respond this need.
The Haar wavelet method, for its mathematically simplicity, computationally efficient and numerically accurate, have been applied for solving integral and differential equations in Refs. [14-16]. In addition, it should be noticed here that the Haar wavelet method is also a valuable tool in structural mechanics problems. Lepik [17, 18] used the Haar wavelet method to study the buckling of elastic beams and vibration characteristics of cracked beams. Zhang and Zhong [19] gave an investigation of a three-dimensional analysis of a simply-supported functionally graded rectangular plate based on the Haar wavelet. The elastic bending problems of orthotropic plates and shells were solved by Majak et al. [20] using this method. Recently, Xie et al. [21, 22] applied the Haar wavelet method to investigate the free vibrations of isotropic and composite cylindrical shells. However, to the knowledge of the authors, it appears that the Haar wavelet method has not been developed to solve the vibration of conical shells with variable thickness.
The motivation of this paper is to investigate vibration characteristics of truncated circular conical shells with variable thickness and present the Haar wavelet method directly to the solution, which simplifies the process presented in Refs. [21, 22]. In the Refs. [21, 22], the integration constants are solved by the matrix form, which makes it hard to solve the problems of the simply or free boundary conditions for conical shells. In this paper, the integration constants are obtained directly from the boundary equations, making it universal to cope with all types of boundary conditions. The governing partial differential equations are established based on the Love first-approximation theory. Then the Haar wavelet method is applied to calculate the natural frequencies and mode shapes of truncated circular conical shells with linearly and parabolically varying thickness. Accuracy of the present method is validated by comparing the present results with the previous studies for both the uniform cylindrical and conical shells. The influences of boundary conditions and geometrical parameters on the free vibration of the conical shells with variable thickness are presented.
2. Theoretical formulation
Consider a truncated circular conical shell as shown in Fig. 1, where is semi-vertex angle, length, and are the radii at two ends. The reference surface of the conical shell is taken to be at its middle surface where an orthogonal coordinate system is fixed. The displacements of the shell are denoted by , and in the meridional , circumferential and normal directions, respectively. The cone radius at any point along its length is given by:
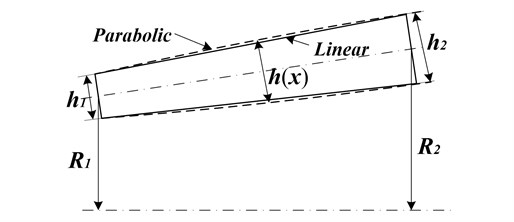
The circular conical shell with variable thickness is shown in Fig. 2, where and are the thickness at the two ends. The thickness can be expressed as [2]:
Fig. 1Geometry of a truncated circular conical shell
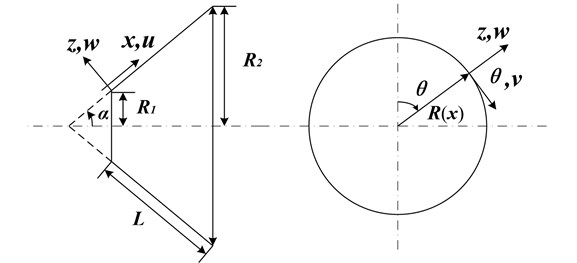
When the value of is extremely large or small, the thickness is suddenly near an edge and such shells are not common in practice. In this paper, the thickness changes linearly for 1, and changes parabolically for2.
The governing equations of free vibration for the truncated circular conical shell based on the Love first-approximation theory can be expressed as follows:
where the expressions of differential operators and are expressed as:
It is worth noting that the expressions of differential operators for conical shells with uniform thickness are the same as given in Refs. [7, 11], and the additional terms are resulted from the variable thickness, which have not been presented in the open literature. The tensile stiffness , bending stiffness are calculated from the following equations:
By the use of separation of variables, the displacement field variables can be expressed as [7]:
where is the angular frequency parameter and is the circumferential wave number. , and are the shape functions along the axes of the displacements and . Substituting expressions of the displacement field Eq. (6) into the governing Eq. (3), and introducing the normalized variable defined by , the following equations can be derived as:
where and are the variable coefficients related to the normalized variable and given in the Appendix A1.
In the present study, the following two types of boundary conditions are considered. The clamped and simply supported boundary conditions can be described as follows [7, 11].
Fig. 2Geometry of a truncated circular conical shell with variable thickness
1. Clamped edge:
2. Simply supported edge:
where and are the frce and moment resultants. They are related to the displacement field in the form:
3. The Haar wavelet method
The Haar wavelets are consisted of piecewise constant functions and are the simplest among all the wavelet families. The Haar wavelet family for [0, 1] is defined as follows [21]:
In Eq. (11), the notations:
are introduced. The quantity is defined, where is the maximal level of resolution. The two parameters and are introduced:0, 1,…, and 0, 1,…, (here the notation is introduced). The wavelet number is defined as . The case1 corresponds to the scaling function: 1 for and 0 elsewhere. The interval [0, 1] is divided into subintervals of equal length ; the collocation points are defined as follows:
In order to apply the Haar wavelet method for further studies, the following integrals of the wavelets in the case are also required [21]:
And in the case 1, we can obtain the integral of the wavelet is .
In the following section, the Haar wavelet method will be in detail presented to show how to apply it to resolve vibration problems of the conical shells. Firstly, the solutions of the displacements , and can be assumed as:
where and are the unknown wavelet coefficients. By integrating Eq. (15) and taking into account Eq. (14), we have:
The eight integration constants in Eq. (16) can be determined from boundary conditions. After discretion by the Haar wavelet method, the forms of the boundary conditions can be described as follows.
1. Clamped edge:
2. Simply supported edge:
Here, we only take the simply supported boundary condition at two ends as an example to present the detailed solution process. According to Eq. (18), the eight additional equations can be written as:
where:
By solving Eq. (19), the eight integration constants in Eq. (16) can be obtained in the following matrix form:
By substituting Eq. (21) into Eq. (16), and taking into account Eq. (15), we can obtain the following matrix forms of all displacement variables and their derivatives:
The detailed expressions of the notations in Eqs. (21) and (22) are given in the Appendix A2. By substituting Eq. (22) into Eq. (7), the following eigenvalue equation with respect to in matrix form can be obtained:
where given by is the vector of unknown variables. and denote the stiffness matrix and mass matrix, respectively. Obviously, solving the standard eigenvalue equation provides the natural frequencies of the conical shells. The mode shapes of , and which corresponds to a certain frequency can be simultaneously obtained by substituting the corresponding eigenvector back into the Eq. (22). The detailed expressions of and can be expressed as follows:
where:
where the matrix for (1, 2,…, 2), and 0 elsewhere.
4. Results and discussions
In the present paper, four sets of boundary conditions are investigated, namely, clamped small edge and clamped large edge (Cs-Cl), clamped small edge and simply supported large edge (Cs-Sl), simply supported small edge and clamped large edge (Ss-Cl) and simply supported small edge and simply supported large edge (Ss-Sl). In the present numerical calculation, a non-dimensional frequency parameter is introduced and defined as:
To validate the accuracy and fast convergence rate of the present method, convergence analysis and comparisons with results available in the literature are performed. The corresponding numerical results are shown in Tables 1-4.
Firstly, the convergence results of the frequency parameter for uniform cylindrical shells, which can be seen as special cases of conical shells, are shown in table 1. The parameters used in the calculations are 0°, 0.3, 10, 1 and 2 or 4, where and denote the order of axial mode and circumferential wave number. By comparing with the exact results in Ref. [23], the series results in Ref. [24] and the DSC results in Ref. [11], the results of the present method are in good accordance with the above-mentioned references. Secondly, in Table 2, the frequency parameter for conical shells with uniform thickness under four typical boundary conditions are considered. The parameters are 45°, 0.3, 0.01, , 0.5, 1 and 3. As can be seen, the present results are generally in agreement with the results obtained by the transfer matrix method in Ref. [1], the GDQ method in Ref. [7] and the element-free kp-Ritz method in Ref. [12]. From tables 1 and 2, it is shown that the convergence of the present method for all the cases is very good. And when the number of is larger than 6, the numerical results change very slightly. Thus, 6 will be used in the following computations.
Table 3 shows the comparison for conical shells with uniform thickness under Cs-Cl boundary conditions and circumferential wave number 1-9, and the other parameters are the same as those in Table 2. As shown in the table, the present results are in good accordance with those in Refs. [1, 7, 12]. However, the results obtained by the Galerkin procedure in Ref. [9] are a little higher than other four results. It may be concluded that the Galerkin procedure for solving the conical shells is not very accurate.
The comparison results of conical shells with uniform thickness under Ss-Sl boundary conditions for different semi-vertex angles are listed in table 4. The parameters are 1, 0.3, 0.01, and 0.25. Again, it can be observed that the solutions of the present method are in good agreement with the reference results.
Table 1Convergence of frequency parameter f for cylindrical shells with C-C boundary conditions (α= 0°, m= 1, μ= 0.3, L/R= 10)
Case | Ref. [23] | Ref. [24] | Ref. [11] | Present | |||
3 | 5 | 6 | 7 | ||||
0.002 (4) | 0.01508 | 0.01515 | 0.01506 | 0.01700 | 0.01522 | 0.01511 | 0.01509 |
0.05 (2) | 0.05787 | 0.05795 | 0.05738 | 0.05931 | 0.05800 | 0.05792 | 0.05791 |
Table 2Convergence of frequency parameters f for conical shells with uniform thickness under different boundary conditions (α= 45°, m= 1, n= 3, μ= 0.3, h2/R2= 0.01, h1=h2, Lsinα/R2=0.5)
Cs-Cl | Cs-Sl | Ss-Cl | Ss-Sl | |
Ref. [1] | 0.5430 | 0.5203 | 0.5249 | 0.5065 |
Ref. [7] | 0.5428 | 0.5201 | 0.5246 | 0.5062 |
Ref. [12] | 0.5428 | 0.5199 | 0.5244 | 0.5061 |
= 2 | 0.5439 | 0.5216 | 0.5262 | 0.5081 |
3 | 0.5430 | 0.5204 | 0.5250 | 0.5067 |
4 | 0.5428 | 0.5202 | 0.5247 | 0.5063 |
5 | 0.5428 | 0.5201 | 0.5247 | 0.5062 |
6 | 0.5428 | 0.5201 | 0.5247 | 0.5062 |
7 | 0.5428 | 0.5201 | 0.5247 | 0.5062 |
Table 3Comparison of frequency parameter f for conical shells with uniform thickness under Cs-Cl boundary conditions (α= 45°, m= 1, μ= 0.3, h2/R2= 0.01, h1=h2, Lsinα/R2= 0.5)
Ref. [1] | Ref. [7] | Ref. [9] | Ref. [12] | Present | |
1 | 0.8120 | 0.8120 | 0.8452 | 0.8120 | 0.8120 |
2 | 0.6696 | 0.6696 | 0.6803 | 0.6696 | 0.6695 |
3 | 0.5430 | 0.5428 | 0.5553 | 0.5428 | 0.5428 |
4 | 0.4570 | 0.4566 | 0.4778 | 0.4565 | 0.4566 |
5 | 0.4095 | 0.4089 | 0.4395 | 0.4088 | 0.4089 |
6 | 0.3970 | 0.3963 | – | 0.3961 | 0.3962 |
7 | 0.4151 | 0.4143 | – | 0.4141 | 0.4141 |
8 | 0.4577 | 0.4568 | – | 0.4567 | 0.4567 |
9 | 0.5186 | 0.5177 | – | 0.5175 | 0.5175 |
From the convergence and comparison studies performed in Tables 1-4, it is concluded that the accurate and convergent results can be obtained using just a few collocation points, which are related to the maximal level of resolution . This conclusion indicates that the present method are numerically accurate and computationally efficient.
Table 4Comparison of frequency parameter f for conical shells with uniform thickness under Ss-Sl boundary conditions (m= 1, μ= 0.3, h2/R2= 0.01, h1=h2, Lsinα/R2= 0.25)
30° | 60° | |||||
Ref. [1] | Ref. [12] | Present | Ref. [1] | Ref. [12] | Present | |
1 | 0.5923 | – | 0.5922 | 0.4754 | – | 0.4754 |
2 | 0.7910 | 0.7909 | 0.7909 | 0.5722 | 0.5719 | 0.5721 |
3 | 0.7284 | 0.7281 | 0.7282 | 0.6001 | 0.5998 | 0.6001 |
4 | 0.6352 | 0.6347 | 0.6349 | 0.6054 | 0.6049 | 0.6053 |
5 | 0.5531 | 0.5522 | 0.5525 | 0.6077 | 0.6071 | 0.6075 |
6 | 0.4949 | 0.4938 | 0.4941 | 0.6159 | 0.6152 | 0.6156 |
7 | 0.4653 | 0.4639 | 0.4643 | 0.6343 | 0.6335 | 0.6340 |
8 | 0.4654 | 0.4629 | 0.4633 | 0.6650 | 0.6641 | 0.6646 |
9 | 0.4892 | 0.4875 | 0.4879 | 0.7084 | 0.7075 | 0.7080 |
The effect of the circumferential wave number n on the vibration frequencies has been studied and the results are shown in Fig. 3. Numerical results given in this figure are obtained by setting 45°, 1, 0.3, 0.01, 0.5 and 0.5. In Fig. 3, the “L” and “P” represent the linearly and parabolically varying thickness, and the following Figs. 4-7 have the same meaning. As shown in this figure, the frequencies for Cs-Cl boundary conditions decrease rapidly for the first few wave number and then increase with the increase of . However, the frequencies for Ss-Sl boundary condition, first increase, then decrease, and again increase with the increase of . This trend is in accordance with the results listed in Table 4. The Cs-Cl boundary conditions provide larger frequency parameter than Ss-Sl boundary conditions. And the difference of frequencies for the two boundary conditions between the linearly and parabolically varying thickness becomes more and more distinct with the increase of . It is concluded that the type of variable thickness has significant quantitative effects on the frequencies when is large.
Fig. 3Variation of the frequency parameter f with respect to circumferential wave number. (α= 45°, m= 1, μ= 0.3, h2/R2= 0.01, h1/h2= 0.5, Lsinα/R2= 0.5)
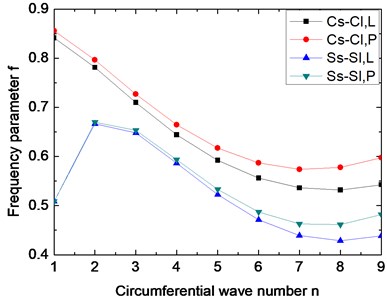
Fig. 4Variation of the frequency parameter f with respect to semivertex angle α. (m= 1, n= 5, μ= 0.3, h2/R2= 0.01, h1/h2= 0.5, Lsinα/R2= 0.5)
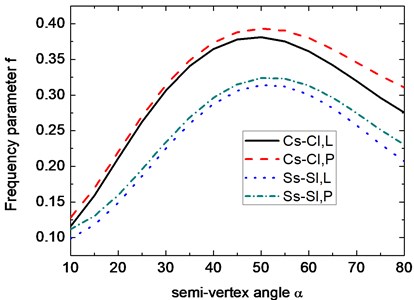
In Fig. 4, the variation of frequency parameter with respect to semi-vertex angle for conical shells with variable thickness under Cs-Cl and Ss-Sl boundary conditions is depicted. The parameters used in this figure are 1, 5, 0.3, 0.01, 0.5 and 0.5. From Fig. 4, it can be observed that a consistent trend for all the two boundary conditions is the same, that is, the frequencies initially increase with the increase of and upon reaching a peak, the frequencies decrease as is further increased. And the peak for the two boundary conditions occurs at almost the same , namely 50°. It also can be seen from Fig. 4 that the difference of frequencies for the two boundary conditions between the linearly and parabolically varying thickness seems more distinct when is larger.
Fig. 5Variation of the frequency parameter f with respect to length-to-radius ratio L/R1. (α= 30°, m= 1, n= 7, μ= 0.3, h2/R1= 0.01, h1/h2= 0.5)
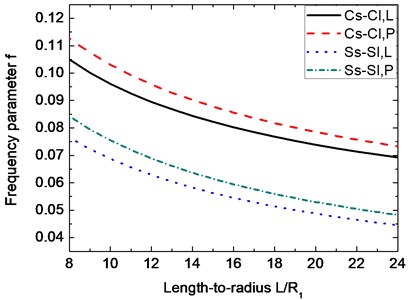
Fig. 6Variation of the frequency parameter f with respect to thickness-to- thickness h1/h2. (α= 30°, m= 1, n= 7, μ= 0.3, h2/R1= 0.01, L/R1= 15)
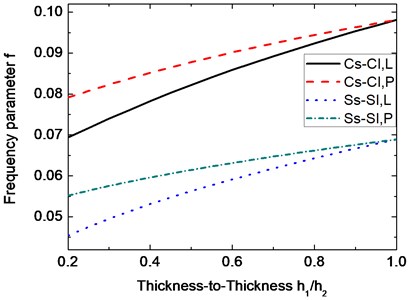
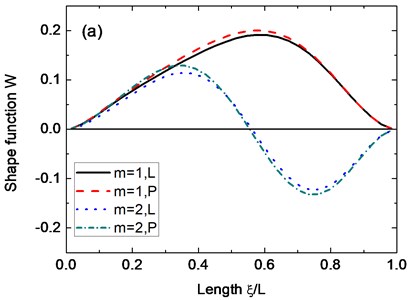
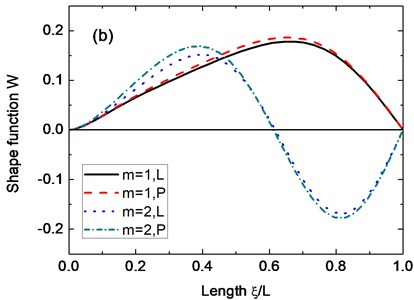
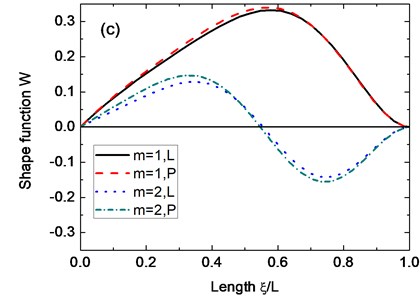
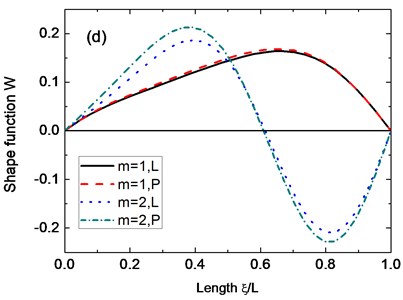
Fig. 7Axial mode shapes of the displacement w under different boundary conditions: a) Cs-Cl; b) Cs-Sl; c) Ss-Cl; d) Ss-Sl. (α= 45°, n= 2, μ= 0.3, h2/R2= 0.01, h1/h2= 0.5, Lsinα/R2=0.5)
Figs. 5 and 6 show the variations of the frequency parameter with length-to-radius ratio and thickness-to- thickness ratio , respectively. The parameters used in Fig. 5 are α=30°, 1, 7, 0.3 0.01, and 0.5. As shown in this figure, the frequencies for the Cs-Cl and Ss-Sl boundary conditions decrease with the increase of . And the difference of frequencies for the two boundary conditions between the linearly and parabolically varying thickness change slightly with the increase of . Results given in Fig. 6 are obtained by setting 30°, 1, 7, 0.3, 0.01 and 15. It can be seen from Fig. 6 that the frequencies for all the Cs-Cl and Ss-Sl boundary conditions increase with the increase of . The difference of frequencies for the two boundary conditions between the linearly and parabolically varying thickness become more and more smaller with the increase of , and the results of the linearly and parabolically varying thickness are the same when 1.
Fig. 7 shows some axial mode shapes of the displacement for conical shells with variable thickness under the Cs-Cl, Cs-Sl, Ss-Cl, and Ss-Sl boundary conditions. The parameters used in this figure are 45°, 2, 0.3, 0.01, 0.5 and 0.5. It can be observed from Fig. 7 that the boundary conditions have much more influence on mode shapes of conical shells than the type of variable thickness. Some circumferential mode shapes of the displacement are presented in Fig. 8. From this figure combined with Fig. 7, the several mode shapes for specific of the conical shells are given and it is believed that these figures can be helpful to understand the vibration behaviors of the conical shells.
Fig. 8The first four circumferential mode shapes of the conical shells; …, undeformed shell
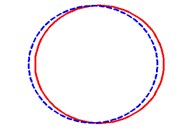
a) 1
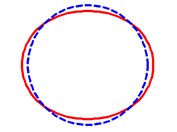
b)2
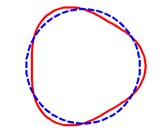
c) 3
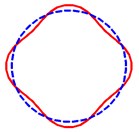
d) 4
5. Conclusions
In this paper, the Haar wavelet method has been successfully extended to study vibration characteristics of truncated circular conical shells with variable thickness under different boundary conditions. Four sets of boundary conditions, that is, Cs-Cl, Cs-Sl, Ss-Cl, and Ss-Sl, are considered in the present study. The accuracy and fast convergence rate of the present method have been validated by convergence studies and comparisons with existing results in the literature. It is concluded that the present method is accurate and efficient for free vibration analysis of conical shells with variable thickness. The effects of geometrical parameters and boundary conditions on vibration characteristics were studied in detail. The advantages of this method consist in its simplicity, fast convergence and high precision. The present method can also be extended to the shells with elastic-support boundary conditions.
References
-
Irie T., Yamada G., Tanaka K. Natural frequencies of truncated conical shells. Journal of Sound and Vibration, Vol. 92, Issue 3, 1984, p. 447-453.
-
Irie T., Yamada G., Kaneko Y. Free vibration of a conical shell with variable thickness. Journal of Sound and Vibration, Vol. 82, Issue 1, 1982, p. 83-94.
-
Sankaranarayanan N., Chandrasekaran K., Ramaiyan G. Free vibrations of laminated conical shells of variable thickness. Journal of Sound and Vibration, Vol. 123, Issue 2, 1988, p. 357-371.
-
Sivadas K. R., Ganesan N. Vibration analysis of laminated conical shells with variable thickness. Journal of Sound and Vibration, Vol. 148, Issue 3, 1991, p. 477-491.
-
Tong L. Y. Free vibration of orthotropic conical shells. International Journal of Engineering Science, Vol. 31, Issue 5, 1993, p. 719-733.
-
Tong L. Y. Free vibration of composite laminated conical shells. International Journal of Engineering Science, Vol. 35, Issue 1, 1993, p. 47-61.
-
Shu C. An efficient approach for free vibration analysis of conical shells. International Journal of Mechanical Sciences, Vol. 38, Issue 8, 1996, p. 935-949.
-
Lam K. Y., Hua L. Influence of boundary conditions on the frequency characteristics of a rotating truncated circular conical shell. Journal of Sound and Vibration, Vol. 223, Issue 2, 1999, p. 171-195.
-
Hua L. Frequency analysis of rotating truncated circular orthotropic conical shells with different boundary conditions. Composites Science and Technology, Vol. 60, Issue 16, 2000, p. 2945-2955.
-
Lam K. Y., Hua L. Orthotropic influence on frequency characteristics of a rotating composite laminated conical shell by the generalized differential quadrature method. International Journal of Solids and Structures, Vol. 38, Issue 22, 2001, p. 3995-4015.
-
Omer C. An efficient method for free vibration analysis of rotating truncated conical shells. International Journal of Pressure Vessels and Piping, Vol. 83, Issue 1, 2006, p. 1-12.
-
Liew K. M., Ng T. Y. Zhao X. Free vibration analysis of conical shells via the element-free kp-Ritz method. Journal of Sound and Vibration, Vol. 281, Issues 3-5, 2005, p. 627-645.
-
Jin G. Y., Ma X. L. Shi S. X., Ye T. G., Liu Z. G. A modified Fourier series solution for vibration analysis of truncated conical shells with general boundary conditions. Applied Acoustics, Vol. 85, 2014, p. 82-96.
-
Lepik Ü. Haar wavelet method for solving higher order differential equations. International Journal of Mathematics and Computation, Vol. 1, 2008, p. 84-94.
-
Hsiao C. Numerical solution of stiff differential equations via Haar wavelets. International Journal of Computer Mathematics, Vol. 82, Issue 9, 2005, p. 1117-1123.
-
Lepik Ü. Solving differential and integral equations by the Haar wavelet method; revisited. International Journal of Mathematics and Computation, Vol. 1, 2008, p. 43-52.
-
Lepik Ü. Buckling of elastic beams by the Haar wavelet method. Estonian Journal of Engineering, Vol. 17, Issue 3, 2011, p. 271-284.
-
Lepik Ü. Exploring vibrations of cracked beams by the Haar wavelet method. Estonian Journal of Engineering, Vol. 18, Issue 1, 2012, p. 58-75.
-
Zhang C., Zhong Z. Three-dimensional analysis of functionally graded plate based on the Haar wavelet method. Acta Mechanica Solida Sinica, Vol. 20, Issue 2, 2007, p. 95-102.
-
Majak J., Pohlak M., Eerme M. Application of the Haar wavelet-based discretization technique to problems of orthotropic plates and shells. Mechanics of Composite Materials, Vol. 45, Issue 6, 2009, p. 631-642.
-
Xie X., Jin G. Y., Liu Z. G. Free vibration analysis of cylindrical shells using the Haar wavelet method. International Journal of Mechanical Sciences, Vol. 77, 2013, p. 47-56.
-
Xie X., Jin G. Y., Yan Y. Q., Shi S. X., Liu Z. G. Free vibration analysis of composite laminated cylindrical shells using the Haar wavelet method. Composite Structures, Vol. 108, 2014, p. 169-177.
-
Dym C. L. Some new results for the vibrations of circular cylinders. Journal of Sound and Vibration, Vol. 29, Issue 2, 1973, p. 189-205.
-
Chung H. Free vibration analysis of circular cylindrical shells. Journal of Sound and Vibration, Vol. 74, Issue 3, 1981, p. 331-350.
Cited by
About this article
This work was supported by the National Basic Research Program of China (Grant No. 2015CB057405) and the National Natural Science Foundation of China (Grant No. 11372082).
