Investigation of modal shapes of the alignment-leveling table

2.1. The object of research

Our proposed alignment and leveling structure is comprised from the table frame (outer ring) containing all other parts of the mechanism; the aligned-leveled disk (inner ring); the bottom ring used for attaching the table to other measurement systems; two alignment-leveling micro-feeds; and the elements for micro-feed transfer (springs, conical nozzles, etc.) (Fig. 1).

The adjustment table of optical and geodesic devices has two pairs of adjustment mechanisms. The position of alignment and leveling is controlled in the same plane, in the two perpendicular axes in relation to one another. This mechanism (Fig. 1 and Fig. 2) differs from the others due to the facility to simplify and increase its accuracy.

Fig. 1The structure of the alignment table: 1 – table frame, 2 – disk, 3 – alignment-leveling micro-feeds

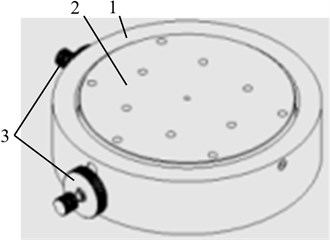
Fig. 23D model section of the table: 1 – table frame, 2 – immobile plate, 3 – moving disk, 4 – frame of alignment-leveling mechanism, 5 – micro screw, 6 – sleeve, 7 – beads, 8 – conical nozzles, 9 – spring, 10 – fixation screw

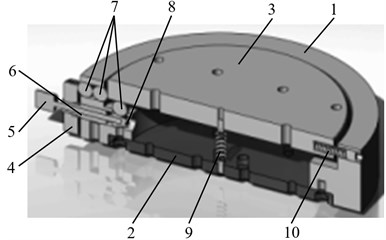
Alignment-leveling micro mechanisms are installed concentrically in the two perpendicular axes and their feed is transferred to the two disc thrusts. In order to increase the displacement accuracy and the resolution of the mechanism, both concentric mechanisms are installed in a way that allows them to operate independently. The alignment position is controlled via two rings; their surface has 0.2 mm incline. In this way they operate concentrically by moving the inner ring through the shots in the right direction. The alignment is done moving a microscope until the disc position corresponds to the rotation position (center-wise).

The leveling position is controlled via two screw cams, which have conical grinded nozzles attached to their bottom. The screws can be rotated to both directions – thus the sliding conical nozzle levels the inner ring into the right position through the shots. The springs support the tightness and keep the disc compacted with the adjustment mechanism. Leveling is also performed while observing the object through a microscope or having an indicator leaning against it till the disc reaches its right position.

2.2. The model of the alignment-leveling table

The behavior of any elastic object interacting with dynamic forces can be specified by the dynamic equilibrium equation [29]:

where $\left[M\right]$, $\left[C\right]$, $\left[K\right]$ are the mass, damping and stiffness matrices, respectively; $\left\{F\right\}$ is the vector of external mechanical forces; $\left\{\ddot{\delta }\right\}=\left\{d^2\delta /d^{2}t\right\}\text{,}$$\left\{\dot{\delta }\right\}=\left\{d\delta /dt\right\}\text{,}$$\left\{\delta \right\}$ are the vectors of accelerations, velocities and displacements, respectively.

For the three dimensional elastic structure, the mass matrix has the form:

where $\rho$ is the density of the material of the structure, $V$ is the volume of the finite element, [$N$] is the matrix of the shape functions of the Lagrange finite element. The stiffness matrix has the form:

where:

and $K=E/3\left(1-2\nu \right),$$G=E/2\left(1+\nu \right),$ where $E$ is the modulus of elasticity and $\nu$ is the Poisson ratio of the elastic material. The damping matrix is assumed as:

where $\alpha$ is the coefficient of external damping and $\beta$ is the coefficient of internal damping. The solution of the system can be approximated by a linear combination of the eigenmodes:

where $\left\{z\right\}$ is the vector of the coefficients of the eigenmodes $z_1$, $z_2$,…, $z_n.$ Modal equations take the form:

where the modal damping is expressed as:

2.3. Active vibroprotection of the alignment-leveling table

It is assumed that the displacement sensors are placed at the nodes of the finite element mesh and correspond to the definite degrees of freedom. Thus the vector of registered displacements is expressed as:

where $\left[S\right]$ is a sensing matrix having one number equal to one in each row and the other numbers equal to zero. It is assumed that the excitation forces act to the nodes of the finite element mesh and correspond to definite degrees of freedom. Thus the force vector is expressed as:

where $\left[E\right]$ is an excitation matrix having one number equal to one in each column and the other numbers equal to zero, $\left\{\stackrel{-}{F}\right\}$ is the vector of forces of excitation sources. It is assumed that the control law corresponds to the following law:

where $\left[T\right]$ is the transformation matrix with constant coefficients. In this case the equations in modal coordinates have the form:

Note that the matrix ${\left[\mathrm{\Delta }\right]}^T\left[E\right]\left[T\right]\left[S\right]\left[\mathrm{\Delta }\right]$ is not diagonal and thus the modal equations are coupled. But by taking into account only the diagonal elements of this equation, it is possible to approximately decouple the system.

In case the velocity (not displacement) sensors are used, the vector of registered velocities is expressed as:

where $\left[S_v\right]$ is a velocity sensing matrix having one number equal to one in each row and the other numbers equal to zero. Then the control can be implemented in accordance to:

where $\left[T_v\right]$ is a velocity transformation matrix with constant coefficients. In that case, the equations in modal coordinates read:

Note that the matrix ${\left[\mathrm{\Delta }\right]}^T\left[E\right]\left[T_v\right]\left[S_v\right]\left[\mathrm{\Delta }\right]$ is not diagonal and thus the modal equations are coupled. But by taking into account only the diagonal elements of this equation, it is possible to approximately decouple the system, and this leads to a much simpler investigation of dynamics of the structure. In this case the total damping matrix has the form ${\left[\mathrm{\Delta }\right]}^T\left[C\right]\left[\mathrm{\Delta }\right]-{\left[\mathrm{\Delta }\right]}^T\left[E\right]\left[T_v\right]\left[S_v\right]\left[\mathrm{\Delta }\right]$. It is recommended to choose the values of elements of the velocity transformation matrix from the condition that the approximately decoupled system would be critically damped. This ensures protection of the investigated table from harmful vibrations.

2.4. Results of investigations of the alignment-leveling table

The upper part of the alignment-leveling table is modelled by using finite element techniques in SolidWorks environment. Table 1 presents leveling table mesh information.

The modeling results are presented below. Fig. 3 shows the first 7 modes of the upper part of the table.

Fig. 3The first 7 modes of the upper part of the table

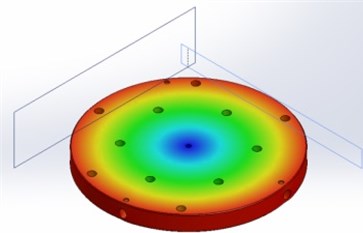
a) 298 Hz frequency

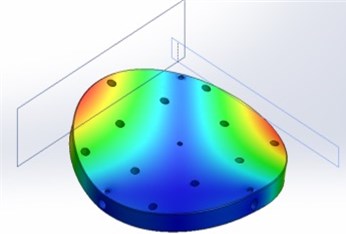
b) 431 Hz frequency

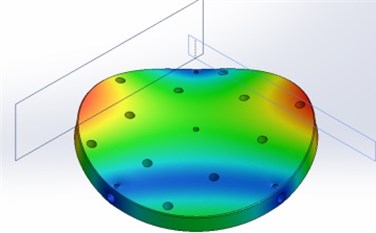
c) 593 Hz frequency

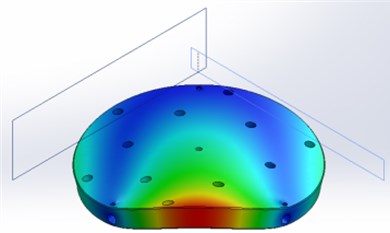
d) 1121 Hz frequency

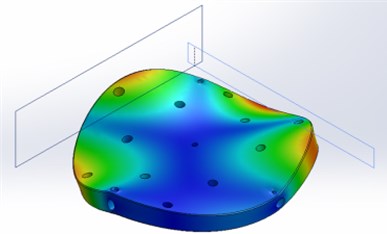
e) 2312 Hz frequency

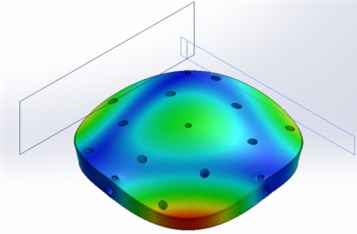
f) 2510 Hz frequency

Table 1Mesh information

Mesh type	Solid mesh
Mesher used	Standard mesh
Automatic transition	Off
Include mesh auto loops	Off
Jacobian points	4 points
Mesh quality	High
Mesh information – details
Total nodes	22811
Total elements	14057
Maximum aspect ratio	12.264
% of elements with aspect ratio < 3	92.6
% of elements with aspect ratio > 10	0.0854
% of distorted elements (Jacobian)	0

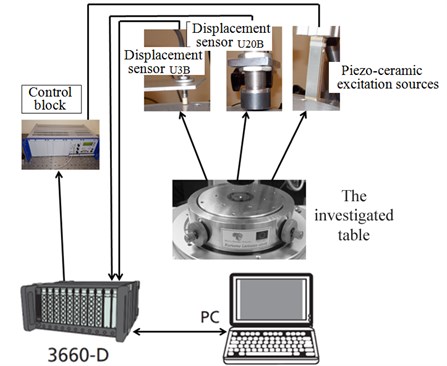
Experimental studies of the alignment table dynamics are performed in order to determine the mechanical instability of the system that influences the quality parameters of the system. For the identification of dynamic mechanical characteristics of the system, the block scheme of the experimental setup is given in Fig. 4; Table 2 shows the comparison between the theoretical and experimental results.

Measurement results show that the dominant frequencies are: 312 Hz, 423 Hz, 570 Hz (frequencies of modes 1, 2 and 3).

Table 2Comparison of theoretical and experimental results of the modal analysis

Modes	Theoretical		Graphical interpretation of measurements of table data using vibration sensors
	Frequency	Eigenmode	Frequency	Eigenmode
1	298		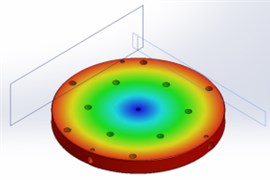312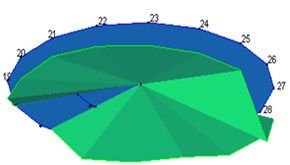
2	431		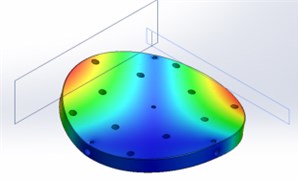423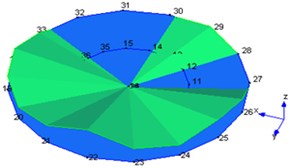
3	593		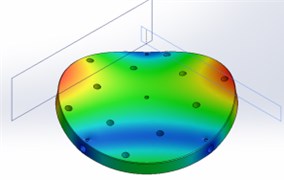570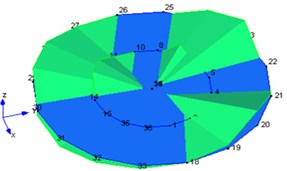

Fig. 4The schematic diagram of the experimental setup