Development of online detection system for natural frequency of brake discs based on the improved least squares complex frequency domain method

2.1. The LSCF method

The LSCF method is based on the common denominator model of the frequency response function [12, 13]. The coefficients of the denominator polynomial are solved by minimizing the error between model and measured data, and then the poles are solved from the eigenvalue of the companion matrix of the polynomial with the solved coefficients. The natural frequency and damping ratio are further solved from the poles.

The common denominator model of frequency response function is:

With $H\left({\omega }_k\right)$ the frequency response function, $k$ ($k=\text{1,}\text{2,…,}{N}_f)$ the serial number, ${\omega }_k$ the $k$-th frequency, $b_r$ and $a_r$ the coefficients of numerator and denominator polynomial respectively, $Z_k$ the polynomial basis function and $2N$ the polynomial order ($N$ the model order of the frequency response function). ${\omega }_k=k∆\omega$, where $∆\omega$ is the frequency resolution. In the LSCF method, a discrete time domain model [11] is applied and let $∆t$ be the discrete time interval, which can be formulated as:

And $Z_k$ can be formulated as:

Replace $H\left({\omega }_k\right)$ with the measured frequency response function $\widehat{H}\left({\omega }_k\right)$ and construct the error function based on Eq. (1) as:

To minimize the value of error function, the least square equation is formulated as:

with $\mathbf{J}=\left[\begin{array}{cc}\mathbf{X}& \mathbf{Y}\end{array}\right]$ and:

To speed up the solving speed of Eq. (5), left multiply it by ${\mathbf{J}}^H$ and reformulate the normal equation as:

With $Re(\bullet )$ the real part component of a complex, $\mathbf{R}=Re\left({\mathbf{X}}^H\mathbf{X}\right)\in {\mathbf{R}}^{(2N+1)\times (2N+1)}\text{,}$$\mathbf{S}=Re\left({\mathbf{X}}^H\mathbf{Y}\right)\in {\mathbf{R}}^{(2N+1)\times (2N+1)}$ and $\mathbf{T}=Re\left({\mathbf{Y}}^H\mathbf{Y}\right)\in {\mathbf{R}}^{(2N+1)\times (2N+1)}\text{.}$ The coefficients of numerator polynomial ${\mathbf{\theta }}_b$ can be expressed by ${\mathbf{\theta }}_a$ from the first row of Eq. (11) as:

Substitute ${\mathbf{\theta }}_b$ into the second row of Eq. (11) and get the reduced normal equation as:

To solve the coefficients of denominator polynomial and get a clarified stabilization diagram, a constraint must be applied to ${\mathbf{\theta }}_a$. Cauberghe et al. [14] studied the relationship between the constraints and poles and pointed out that the constraint equation $a_{2N}=\text{1}$ results in the damping ratio of mathematic poles negative. The physical poles can be effectively selected from mathematic poles based on this. So, the coefficients of denominator polynomial ${\mathbf{\theta }}_a$ can be solved by substituting $a_{2N}=\text{1}$ into Eq. (13).

With ${\mathbf{\theta }}_a$ determined, Eq. (14) corresponding to the denominator polynomial can be solved:

And the poles are solved from the roots of Eq. (14). However, when the model order is too high, it is difficult to solve the equation directly. The problem about solving the poles of the frequency response function can be transformed into solving the eigenvalue of the companion matrix of the polynomial with coefficients ${\mathbf{\theta }}_a$. Decompose matrix $\mathbf{A}$ by the eigenvalue as:

With $\mathrm{\Phi }$ the eigenvector matrix, $\mathbf{\Lambda }$ the diagonal matrix with eigenvalues. The roots of Eq. (14) are in the diagonal line of eigenvalue matrix $\mathbf{\Lambda }$, and ${\mathbf{\Lambda }}_i=e^{{\lambda }_i\mathrm{\Delta }t}$, where ${\mathbf{\Lambda }}_i$ is the $i$-th eigenvalue and ${\lambda }_i$ is the corresponding pole. The natural frequency and damping ratio can be solved from the real and imaginary parts of ${\lambda }_i$.

A certain type of brake disc is detected to extract the frequency response function as an example. The stabilization diagram by the LSCF method is shown as Fig. 1.

Fig. 1Stabilization diagram of the LSCF method (◇: both frequency and damping ratio stable; ▽: only frequency stable)

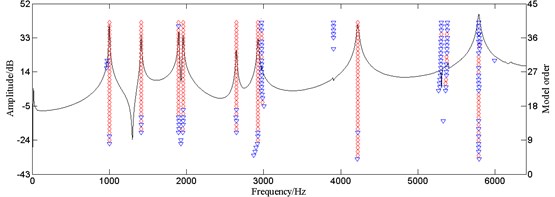
The red diamond indicates poles that are stable in both frequency and damping ratio, and the inverse blue triangle indicates poles only stable in frequency. The stability of poles is determined by the change rate of frequency and damping ratio of adjacent model order. If both of them are in the tolerance ranges, the pole is seen as stable pole. If only the frequency change ratio is in the tolerance range, the pole is seen as only frequency stable pole. If the occurrence number of both frequency and damping ratio stable pole, that’s the number of red diamond in a certain column of the stabilization diagram, is one-third greater than the maximum model order, the corresponding frequency is seen as natural frequency, or the poles are seen as only frequency stable poles. The occurrence of only frequency stable poles is very likely to cause error in natural frequency extraction.

The identification result is credible for the poles steadily appear in the peaks of the frequency response function curve as shown in Fig. 1. However, there are many only frequency stable poles at about 2960 Hz, 3898 Hz, 5276 Hz, and 5372 Hz, which appear as small peaks. Small peaks are sensitive to the small change of excitation positions and SNR, so they are not acceptable to be the criteria of online detection. Besides, noise interference does harm to the accuracy of online detection. So, it is necessary to apply the truncated SVD algorithm to the LSCF method for noise reduction, thus increasing its accuracy and anti-noise interference ability.

2.2. Truncated SVD for noise reduction

In signal processing, SVD has been proved to be an effective method for noise reduction by restraining small signal components to enhance large components [15]. Considering that the SVD is completed in the time domain, the frequency response function is firstly transformed to impulse response function. And after the noise reduction is done, the processed signal is transformed back into the frequency domain for modal parameter identification by the LSCF method.

Based on the theory of phase space reconstruction [16], the transformed impulse response function can be seen as the original signal $h\left(t_k\right)(k=\text{1,}\text{2,…,}{N}_f)$ with noise interference. When it is mapped into a $m\times n(m<n)$ demission phase space, the reconstructed phase space orbit matrix ${\mathbf{D}}_H$ is:

Obviously, ${\mathbf{D}}_H$ is a Hankel matrix and $m+n-1=N_f$.

Matrix ${\mathbf{D}}_H$ indicates the evolution properties of reconstructed attractor in phase space and can be expressed as: ${\mathbf{D}}_H=\mathbf{D}+\mathbf{W}$, with $\mathbf{D}$ and $\mathbf{W}$, the orbit matrices of signal and noise respectively. So, the noise reduction for initial signal becomes the finding of optimal approximation for $\mathbf{D}$, with ${\mathbf{D}}_H$ known ahead. Decompose matrix ${\mathbf{D}}_H$ by the singular value as:

With $\mathbf{U}$, $m\times m$ demission unitary matrix, $\mathbf{V}$, $n\times n$demission unitary matrix, and $\mathbf{S}$, $m\times n$ demission positive semi-definite matrix. The singular values of ${\mathbf{D}}_H$ are in the diagonal of $\mathbf{S}$ with large to small arrangement. Truncate the first $p$ larger singular values while the rest are set as 0, and matrix ${\mathbf{D}}_H^{\text{'}}$ is got from the inverse process of SVD by the equation: ${\mathbf{D}}_H^{\text{'}}=\mathbf{U}\times {\mathbf{S}}_p\times {\mathbf{V}}^H$, where ${\mathbf{S}}_p$ is the truncated $m\times n$ demission matrix. Then, matrix ${\mathbf{D}}_H^{\text{'}}$ is the optimal approximation to orbit matrix ${\mathbf{D}}_H$ with truncated order $p$, and noise is reduced at some degree. The order to be truncated in SVD is determined by the increment of singular entropy [17]. The singular entropy of truncated signal can be expressed as:

With $∆E_i$ the increment in the $i$-th order and can be calculated by:

With ${\lambda }_i$ the $i$-th larger singular value. When a wide-band noise interferes in the signal, the singular entropy grows with the model order and the growing speed slows down at a certain value, where the effective feature information is almost saturate and the following increase of the singular entropy comes from noise. So, the chosen order for truncation is located at the slowed down order. In other words, the truncation order is determined by the value of $∆E_i$, thus reserving effective signal component and removing noise component.

Generally, matrix ${\mathbf{D}}_H^{\text{'}}$ is no longer a Hankel matrix and to get the de-noised signal matrix $h^{\text{'}}\left(t_k\right)$, the back-diagonal values of ${\mathbf{D}}_H^{\text{'}}$ are averaged as Eq. (20). To simplify the calculation, the $m\times n$ demission matrix ${\mathbf{D}}_H^{\text{'}}$ is lower right zero padded to a $N_f\times N_f$ demission matrix $\widehat{{\mathbf{D}}_H^{\text{'}}}$:

Fig. 2Stabilization diagram of the LSCF method with truncated SVD (◇: both frequency and damping ratio stable; ▽: only frequency stable)

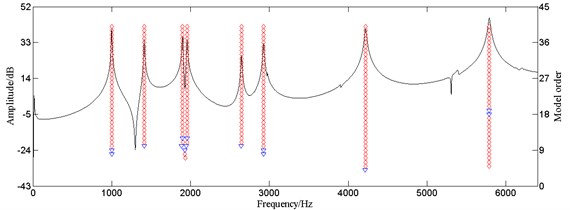
Till then, transform the time domain signal $h^{\text{'}}\left(t_k\right)$ back into the frequency domain as a new frequency response function and the modal parameters can be extracted by the LSCF method.

The frequency response function of brake disc from Fig. 1 is set as an example. The proposed algorithm, truncated SVD for noise reduction and the LSCF method for modal parameter identification, is applied to it. Stabilization diagram from that algorithm is shown as Fig. 2 and modal parameters are extracted in Table 1. It clearly shows that this algorithm effectively restrained small peaks and noise and the stabilization diagram is more clear and accurate than Fig. 1.

4.1. Program development

The developed system is based on the mixed programming of VB and MATLAB. It mainly realizes the control and parameter settings of PULSE Lab Shop, the extraction of frequency response function, the identification of modal parameters, the qualified evaluation and data storage management. The frequency response function is extracted from PULSE Lab shop by VB and the LSCF method based on SVD developed by MATLAB is compiled by MATCOM into DLL file that can be called by VB. So, the parameter identification can be done in online detection process. The software flow chart is shown as Fig. 4.

Fig. 3Stabilization diagram of the LSCF method with truncated SVD under different SNR (◇: both frequency and damping ratio stable; ▽: only frequency stable)

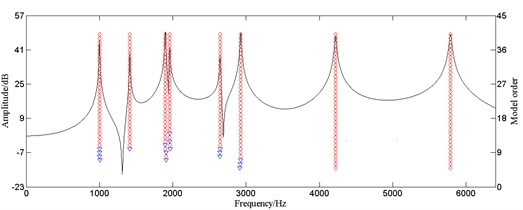
a) Without noise

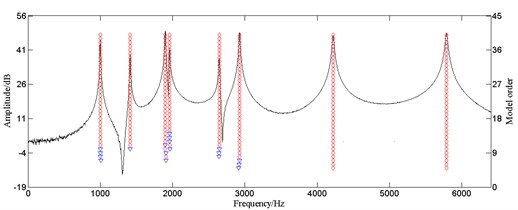
b) SNR = 50 dB

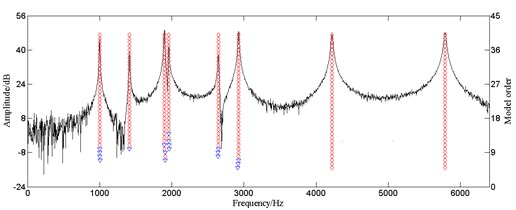
c) SNR = 30 dB

Fig. 4Flow chart of main program

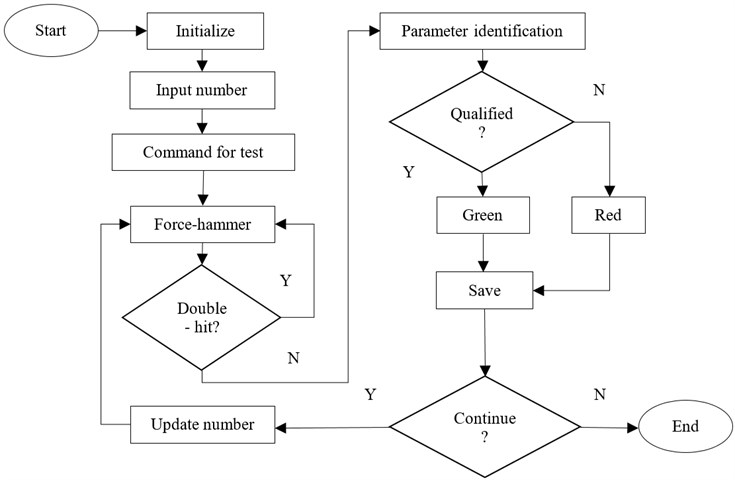
When the software works, PLUSE Lab Shop is firstly opened and the measurement parameters in the configuration file are read out and the system is initialized. This system saves all of the attribute parameters and testing numbers in form of configuration file, so the setting of constraint parameters and testing numbers are only necessary in the first detection of a new product. When clicking the start button, the software will send command to PULSE for detection and wait for excitation from force hammer. When the force signal and the corresponding acceleration signal are detected, the force signal is extracted for double hit detection. If double hit exists, the system will back to waiting for a new excitation from force-hammer, if not, the frequency response function will be extracted for modal parameter identification. Then, the extracted natural frequencies and reference natural frequencies are compared and qualification judgment is made. Finally, the qualified rate will be counted and saved automatically, and the frequency response function curve, double hit detection curve, natural frequencies and qualified result will be shown in the ‘Live Report’ that embedded in the main interface. The system has a continuously automatic detection principle that it updates the testing number and back to waiting for pulse excitation automatically, so the running efficiency is high. The main graphical user interface of this software is shown as Fig. 5.

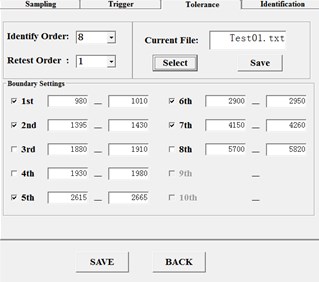
Small peaks in the frequency response function of brake discs are sensitive to the small change of excitation positions and if the corresponding frequencies are set as references, there might be misjudge. So, in this system, the frequencies that steadily appear and not easily affected by the small change of excitation positions are selected as references manually. If the corresponding natural frequencies are in the tolerance range, the product is judged as qualified. The Graphical user interface of tolerance settings is shown as Fig. 6.

Fig. 5Main graphical user interface of the software

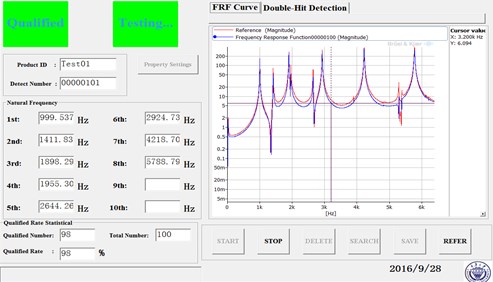
Fig. 6Graphical user interface of tolerance settings

4.2. Parametric control

For the convenience of adjusting constraint parameters according to different detection objects and user requirements, the key parameters are controlled in form of configuration file. This parametric control extends the application range of the system. The key parameters include the frequency range, the maximum model order and steady parameters.

The setting of frequency range not only defines the frequency width for parameter identification, but also constraints the data base that constructs the least square equations in LSCF algorithm. The sample capacity is required to be far more than two times the model order to avoid ill-conditioned functions.

The maximum model order is the maximum function order to be cyclically solved in LSCF algorithm. The model order should be as large as 30-50 to contain enough information of frequency response function and get more stable poles.

Steady parameters include the absolute and relative value of damping ratio tolerance and the relative value of frequency tolerance. The absolute value of damping ratio tolerance that usually at a small value is the upper limit of damping ratio. It is determined by the damping characteristic of the detected object. The relative value of frequency tolerance and damping ratio tolerance determine the stability of a pole, and the setting of the latter is often higher than the former for the frequency is easier to be stable because of its higher pure value. In this online detection system, the default setting tolerances of absolute and relative damping ratio and relative frequency are 10 %, 5 % and 1 % respectively.