Abstract
The vibration excitation of the rolling mill mainly comes from the gearbox in the process of rolling strip, and the meshing excitation is the main excitation factor of the gearbox. And the gear backlash plays an important role in the meshing excitation. However, the backlash is inevitable in the process of designing the gear system. Therefore, it is important to select the appropriate gear backlash to reduce the vibration amplitude of the gearbox, to improve the rolling speed and the quality of the steel strip. So, in this paper, the effect of the different variation amplitudes for the time-varying gear backlash (TVGB) on the vibration characteristics of the gear system under various mesh parameters is studied. A new formulation for calculating nonlinear damping and time varying meshing stiffness is applied in this coupling model. The results show that increasing of the load torque, the damping ratio, the system parameter or decreasing the directional rotation radius variation or kinematic transmission error caused the effects of variation amplitudes for the (TVGB) on the dynamic characteristics of the gear system to decrease. Test data from a gearbox experimental table verifies the accuracy of the model. The model is shown to be capable of simulating the mutually coupled effect between the backlash and the different parameters on the gear system. So, the new coupled model can be used as guide to select the appropriate gear backlash values for the rolling mill under different operating conditions.
1. Introduction
With advances in the industry, the requirements for cold rolling mills in terms of strip yield and strip surface quality have become more stringent. In cold rolling mills, increasing the speed increases the yield, but the vibrations must be reduced to improve the quality of the product. High speeds increase vibrations, and thus the probability of failure, which decreases the profitability of a mill. For example, in a cold-rolling mill operated by WISCO (Wuhan Iron and Steel Corporation), a roller locked fault in the fourth stand caused breaking of the bolt that connected the upper and lower sections of the gearbox housing. The mill had to be shut down for 48 hours, resulting in a loss of tens of millions of RMB and may have caused additional undetected problems. Therefore, methods for reducing the gearbox vibration amplitude and failure rate and for improving the product quality and production efficiency are important to the industry.
One effective method to reduce the gearbox vibration amplitude consists in the direct reduction of the gear system vibration amplitude. So, the vibration mechanism of gearbox has attracted significant attention from the research community. Most of the scholars think that the vibration of meshing excitation is the main reason that causes the vibration of the gearbox. However, the vibration characteristics for the gear system are very complicated and hardly controllable because it is very sensitive to the time-varying gear backlash, and the overall structural characteristics. Therefore, getting a more thorough comprehension of the dynamics characteristics for the gear system is essential in the research of gearbox vibration mechanism. A. Guerine studied the dynamic response of a spur gear system with uncertain friction coefficient [1]. J. G. Wang [2] studied the nonlinear dynamics analysis of the spur gear system for a railway locomotive. And in his article the static transmission error and time-varying meshing stiffness have been considered. And the dynamic characteristics of the gear system affected by other factors had been studied by other scholars [3-7]. Some scholars [8-11] studied the dynamic characteristic affected by the gear backlash. They usually set gear backlash as a fixed value or a steady random number which meets the normal distribution Q. Chen [12] studied the gear system dynamic characteristics affected by the gear backlash based on the fractal theory. In his article, he studied the effect of backlash on the gear system. However, in his article, the gear backlash was assumed to have a constant value. Teik C. Lim [13] presented a generalized nonlinear time-varying dynamic model of a hypoid gear pair. In this article, he studied the dynamic characteristics of the gear system affected by different time-varying parameters. However, in the actual gear system, the influence of gear backlash and the variation of the parameters on the vibration characteristics of the gear system are mutually coupled.
Although many scholars have achieved rich research results, previous studies have focused on the vibration characteristic of only various mesh parameters or the gear backlash. And the gear backlash usually took a constant value. Actually, mesh parameters can affect not only the vibration characteristics of the gear system or the variation amplitudes of gear time-varying backlash, and the variation amplitudes of gear time-varying backlash can also affect the mesh parameters. Such as the dynamic transmission error can affect the variation amplitudes of gear time-varying backlash. And the variation amplitudes of gear time-varying backlash can affect the dynamic transmission error. Therefore, the development of a coupling model between the different variation amplitudes for the (TVGB) and the mesh parameters is very important. Such a model would not only allow the vibration amplitude of the gear system to be determined more accurately but also could find the gear system vibration source more comprehensively to reduce vibration amplitudes of the gear system.
2. Traditional dynamic model of the gear system under different mesh parameters
2.1. Model of the traditional gear system
The traditional gear system is shown in Fig. 1. In this model, the big gear and pinion is simulated by rigid body, and by taking the rotation displacement as their coordinate system. Meshing gears are simplified with an equivalent stiffness and damping. The gear backlash is assumed to have a value of . The dynamic transmission error is expressed as.
Fig. 1Traditional gear system model
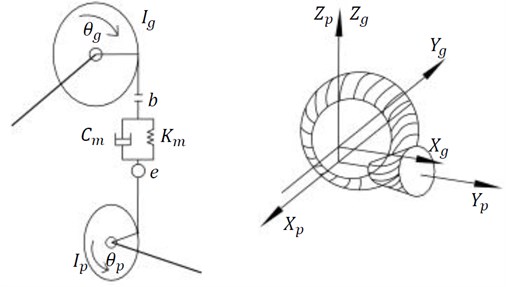
2.2. Mathematical model of the traditional gear system
where and are the mass moments of pinion and gear respectively, and are the corner of pinion and gear respectively, is the mean load torques on the big gear. is the time mean load torque on the pinion. is the mean mesh stiffness, , are the orientation-rotating radiuses of big gear and pinion respectively:
where , is the system parameter, is the mesh damping ratio, is the dynamic transmission error, is the gear backlash which is assumed to have a constant value. The traditional model was formulated to study the effect of the various parameters such as the load, the damping ratio, the orientation rotating radius, system parameters and the dynamic transmission error on the vibration characteristics of the gear system. And the calculation method of meshing stiffness in this model is based on the Fourier expansion.
3. Coupling nonlinear dynamics model of the gear system
3.1. The coupling nonlinear dynamics model of the gear system
In the actual meshing process, the backlash of gear system is time-varying. The variation amplitudes for the gear backlash with time-varying have a great influence on the vibration amplitude of gear system. So, in the present study, a modified coupling model which improves the original model assuming that the backlash is constant value is developed to study the effect of variation amplitudes for the (TVGB) on the vibration characteristics of gear system under various mesh parameters. The coupling model is shown in Fig. 2. A method for solving gear meshing stiffness based on the energy method is formulated in the coupling model, improving the traditional model based on the Fourier expansion to solve the meshing stiffness of the gear system. The new method makes the solution results closer to the meshing stiffness of the actual gear system meshing process. At the same time, a nonlinear damping calculation method is applied to solve the damping of gear system.
Fig. 2a) A-coupling torsion vibration model of the gear system model, b) 3D model for interaction between two rotating shafts
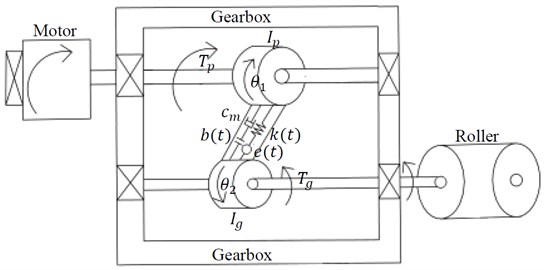
a)
b)
3.2. Mathematical model of modified coupling gear system
The coupling model of the gear system is proposed in this paper, as shown in Figure-2. The equations of the model are derived as follows:
where and are the pinion and gear respectively. is the time-varying mesh stiffness. is the nonlinear damping. is the variation amplitudes for the (TVGB). is the dynamic transmission error. And the nonlinear displacement function is shown below:
The existing backlash can make the tooth separation and impacts, so it can have an important effect on the vibration characteristics of the gear system. The backlash is time-varying in the actual meshing, owing to the tooth meshing impact, tooth deformation, manufacturing error and the presence of wear. The variation amplitudes for the (TVGB) are expressed as follows:
where is the amplitude of the backlash, 0, 1,…, . is the corresponding frequency. The equation of the modified coupling gear system model is expressed as Eq. (10):
where , is equivalent mass, is nonlinear damping and the calculation method is shown in 3.3, is time-varying mesh stiffness and the calculation method is shown in 3.4:
Next, the following sets of dimensionless parameters are assumed below:
where , are the dimensionless orientation rotating radius of pinion and gear, and its expression is shown in Eqs. (20), (21). is the dimensionless dynamic transmission error.
So a coupling nonlinear dynamics model of the gear system of Eq. (10) can be expressed as Eq. (13):
where is the torque acting on the input shaft of the gear system. is the torque acting on the output shaft of the gear system. is the average mesh stiffness,, are the mean orientation rotating radius of pinion and gear. Some dimensionless parameters such as the dynamic transmission error can be expressed as the Fourier series. is the dimensionless system parameter, is the dimensionless mesh damping ratio, is the dimensionless average load torques on the big gear, is the dimensionless load torques on the pinion:
Taking Eqs. (20-22) into (13), The coupling model between the variation amplitudes for the (TVGB) and the different time-varying mesh parameters of the gear system can be obtained:
3.3. Calculation of nonlinear damping
The overall nonlinear mesh damping is composed of three parts. The first part () is the system part, and it is proportional to the load when it was adjusted [14]. The second part is hysteresis () damping, and it is affected by the deformation of the material [15]. The third part is affected by the oil squeeze:
where represents all the damping caused by the gear pairs, represents the total hysteresis damping of gear pair I, is the hysteresis damping caused by the deformation for tooth j of pair I. represents the contacting hysteresis damping for the gear pair I:
where, represents half of contact width (m); represents the tooth face width; represents the dynamic viscosity:
represents the Newtonian lubricants viscosity at low rates; represents the Newtonian lubricants viscosity at high rates; where is the rotational relaxation time of a molecule. represents the number of contacting teeth; is a modulus which represented by the shearing stress in the beginning of the transmission; is the power-law exponent; represents the film thickness, it usually can be thought as the central film thickness :
where represents the load per unit width (N/m), is the equivalent curvature radius, is the composite modulus, is the fluid entraining velocity, is the dynamic viscosity at atmospheric pressure, is the pressure-viscosity coefficient.
3.4. Calculation of time-varying meshing stiffness
Xinhao Tian [16] pointed out that the potential energy stored in the gear included five parts when calculating the time-varying mesh stiffness of gear pair based on the energy method. Hertz energy bending energy radial compression energy and shear energy fillet-foundation stiffness , they can be used to calculate the Hertz stiffness , bending stiffness , radial compression stiffness , and shear stiffness . Those stiffness can be expressed as follows:
where is the elastic modulus; is the axial thickness of gear, and is the Poisson’s ratio. is the half of the base tooth angle. , , , and shear stiffness are the four parts of gear stiffness. The fillet-foundation stiffness is investigated in the reference [17]:
where the coefficients , , and can be represented below:
is the polynomial function; ; where is the root circle radius. the physical significance of , and is shown in Fig. 3; and the values of , , , , and are shown in Table 1.
Fig. 3Geometric parameters of gear deformation
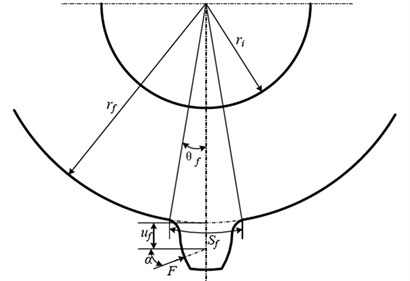
Table 1Coefficients value [18]
–5.574×10-5 | 60.111×10-5 | –50.952×10-5 | –6.2042×10-5 | |
–1.9986×10-3 | 28.100×10-3 | 185.50×10-3 | 9.0889×10-3 | |
–2.3015×10-4 | –83.431×10-4 | 0.0538×10-4 | –4.0964×10-4 | |
–4.7702×10-3 | –9.9256×10-3 | 53.300×10-3 | 7.8297×10-3 | |
0.0271 | 0.1624 | 0.2895 | –0.1472 | |
6.8045 | 0.9086 | 0.9236 | 0.6904 |
The meshing stiffness for the meshing tooth can be expressed by Hertz stiffness , bending stiffness compression stiffness in the radial direction shearing stiffness and fillet-foundation stiffness . The result is shown below:
where is the teeth pair for a gear pair.
Table 2Baseline system parameters which we uses in this paper [13]
Number of pinion teeth | 30 |
Number of gear teeth | 41 |
Gear pitch radius (m) | 0.168 |
Pinion pitch radius (m) | 0.048 |
Mass moment of inertia of pinion (kg∙m2) | 0.002 |
Mass moment of inertia of gear (kg∙m2) | 0.05 |
Mean backlash (mm) | 20 |
Mean mesh damping ratio | 0.03 |
4. Simulation results and discussion
In most cases has a little difference from , so we think =. For the following numerical simulation studies, the basic data values are shown in below.2, 0.03, 0.01, 0, 1/2. By solving the root-mean-square value of Eq. (23), we can obtain the frequency response (). The solution results are shown below.
4.1. Effect of the variation amplitudes for the (TVGB) on the dynamic characteristics of the gear system under various load torques
The coupling effect of the load torques and the variation amplitudes for the (TVGB) on the gear system is shown in Fig. 4. Where the abscissa is the dimensionless speed and the ordinate is the root mean square value of the gear system vibration.
Fig. 4Effect of variation amplitudes for the (TVGB) on the dynamic response of the gear system under the different load torques
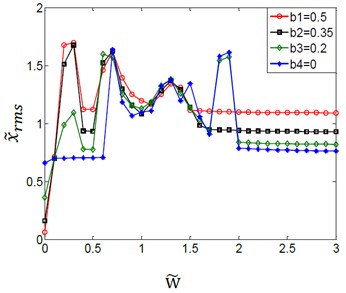
a)0.1
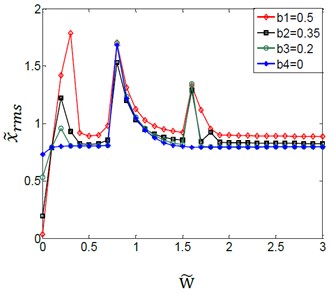
b)0.6
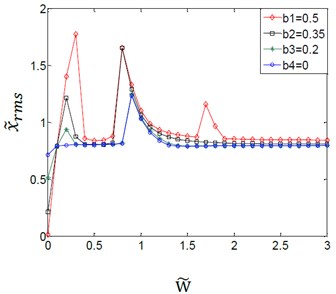
c)0.8
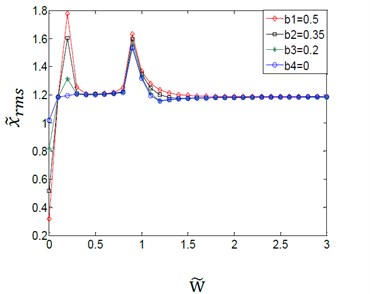
d)1.2
We can see from Fig. 4(a)-(d) that the effect of the variation amplitudes for the (TVGB) on the gear system tends to decrease, and the overall jump discontinuity is more linear with increasing of the mean load torque. In Fig. 4(a), the speed of the first vibration jump is 0.7 when the variation amplitude of gear backlash () is assumed to have a value of 0, but the speed is 0.2 when the is assumed to have a value of 0.2, 0.35 or 0.5. And the gear system will be in a steady state only when the speed reaches to 2.1. When load torque increases to 0.6 as shown in Fig. 4(b), under this load torque the effect of the variation amplitudes for the (TVGB) on the gear system is smaller than that when the load torque is 0.1. When the load torques increases to 0.8 as shown in Fig. 4(c), the gear system reaches a steady state after two times of vibration jump and the third vibration jump emerges only when the variation amplitude of gear backlash is 0.5. When the load torque increases to 1.2 as shown Fig. 4(d), the variation amplitudes for the (TVGB) affect the vibration amplitude of the gear system only at a relatively low speed. The influence of the variation amplitudes for the (TVGB) on the gear system is gradually disappeared with increasing speed. The reason is that the load torque becomes large enough, thus preventing the separation of the teeth, and resulting in that the value of the variation amplitude of gear backlash () is almost equal to zero. These effects can eliminate the effect of the variation amplitudes for the (TVGB) on the gear system. Clearly from these results, the effect of the variation amplitudes for the (TVGB) on the gear system tends to decrease with increasing of load torques. The first speed, the amplitude and the numbers of vibration jumps which affected by the variation amplitudes for the (TVGB) gradually decrease with increasing of the load torques.
4.2. Effect of the variation amplitudes for the (TVGB) on the dynamic characteristics of the gear system under the different damping ratio
The dimensionless damping ratio can be derived using Eq. (16). With the other parameters hold constant, the vibration amplitudes of the gear system for various damping ratio are obtained. The simulation results are shown in Fig. 5.
Fig. 5Effect of variation amplitudes for the (TVGB) on the dynamic response of the gear system under the different damping ratio
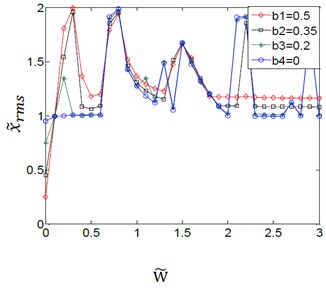
a)0.01
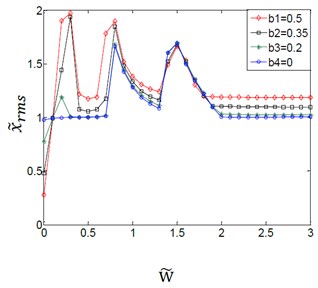
b)0.03
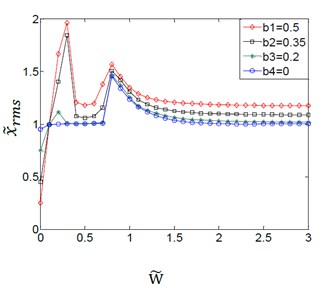
c)0.06
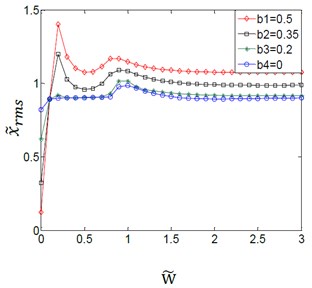
d)0.12
Fig. 5(a)-(d) shows the coupling effect between the variation amplitudes for the (TVGB) and the different damping ratios on the gear system. It can be seen that the effect of the variation amplitudes for the (TVGB) on the gear system tends to decrease, and the overall jump discontinuity is more linear with increasing of the damping ratio. When the damping ratio is 0.01 as shown in Fig. 5(a), an increase in variation amplitudes for the (TVGB) causes the numbers of vibration jumps to increase. The variation amplitudes for the (TVGB) are the main factor which affects the characteristics of vibration jumps of the gear system. When the damping ratio increases to 0.03 as shown in Fig. 5(b), the effect of the variation amplitudes for the (TVGB) on the gear system is more reduced than that when the damping ratio is 0.01. And the numbers of vibration jumps are three times, which is less than that when the damping ratio is 0.01. When the damping ratio increases to 0.06 as shown in Fig. 5(c), the numbers of vibration jumps are two times which is smaller than that when the damping ratio is 0.03. When the damping ratio increases to 0.12 as shown in Fig. 5(d), the amplitude of vibration jump which effected by the variation amplitudes for the (TVGB) are very small. And the overall vibration response appears to be linear. The effect of the variation amplitudes for the (TVGB) on the gear system is gradually disappeared with increasing of the speed. No impacts and jump discontinuities are observed under this damping ratio because an increase in damping ratio causes the torques of the gear system to increase, resulting in that the torques become large enough and thus the tooth separation can be prevented. These effects eliminate the effect of the variation amplitudes for the (TVGB) on the gear system. Hence, it can be seen from these results that the effect of the variation amplitudes for the (TVGB) on the gear system tends to decrease with increasing of the damping ratio. With increasing of the damping ratio, the amplitude, the first speed and the numbers of vibration jumps which affected by the variation amplitudes for the (TVGB) gradually decrease.
4.3. Effect of the variation amplitudes for the (TVGB) on the dynamic characteristics of the gear system under the different time-varying variation in directional rotation radius
Here we only consider the basic harmonic form of the . The variation of is mainly owing to the change of the mesh point space position. And the tooth errors, gear eccentricity and shaft misalignment are the main factors which affect the .
Fig. 6Effect of variation amplitudes for the (TVGB) on the dynamic response of the gear system under the different directional rotation radius variation
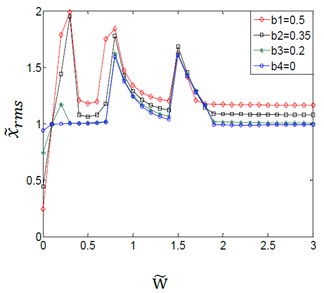
a)0.005
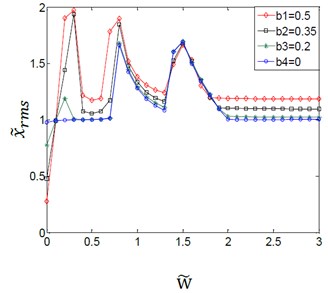
b)0.015
c)0.03
It can be seen from the Fig. 6. The effect of the variation amplitudes for the (TVGB) on the critical speed of the gear system (when the gear system reaches a stable state) gradually increases with increasing of the rotation radius. But the effects of the variation amplitudes for the (TVGB) on the vibration jump numbers and the vibration amplitude have little changes with increasing of the directional rotation radius variation. The reason is that the variation of the directional rotation radius is caused by the change of the space position of the mesh point. And the change of the mesh point has a little effect on the variation amplitudes of the gear backlash. The value of the is very small, and it’s usually take the range of 0.003-0.02 for most of gear systems which we have studied. These effects reduce the effect of variation amplitudes for the (TVGB) on the gear system. So, under the normal condition, the variation amplitudes for the (TVGB) has a little influence on the dynamic characteristics of gear system with increasing of the directional rotation radius variation.
4.4. Effect of the variation amplitudes for the (TVGB) on the dynamic characteristics of the gear system under the different system parameter
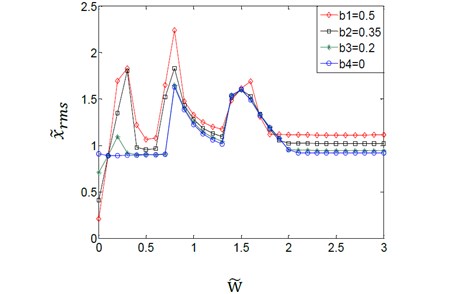
The system parameter can be calculated from the given Eq. (17). And the couple effect of the system parameter and the variation amplitudes for the (TVGB) on the gear system is shown in Fig. 7.
Fig. 7Effect of variation amplitudes for the (TVGB) on the dynamic response of the gear system under the different system parameter
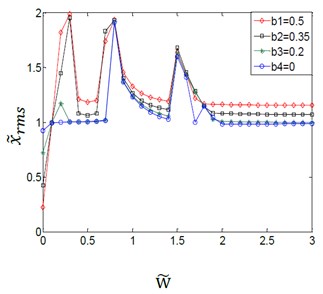
a)0.03
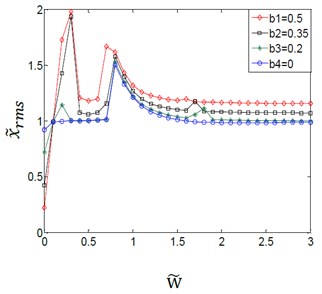
b)1.5
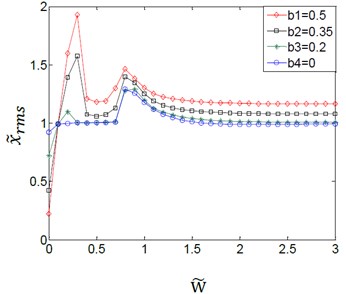
c)3.0
From Fig. 7(a)-(c), it can be seen that the couple effect between variation amplitudes for the (TVGB) and the different system parameters on the vibration characteristics of the gear system is the same with the couple effect between the variation amplitudes for the (TVGB) and the different damping ratio. The effect of the variation amplitudes for the (TVGB) on the gear system tends to decrease with increasing of the system parameter. The first speed, the amplitude and the numbers of vibration jumps which affected by the variation amplitudes for the (TVGB) gradually decrease with increasing of the system parameter.
4.5. Effect of the variation amplitudes for the (TVGB) on the dynamic characteristics of the gear system under the various time-varying dynamic transmission errors
The dynamic transmission error is caused owing to the displacement excitation at the meshing points. The reason is that the change of the meshing point moves along the direction of the action line, resulting in a great effect on the variation amplitudes of the gear backlash. So, if transmission error exists, the variation amplitudes for the (TVGB) play an important role in affecting the dynamic characteristics of the gear system.
Fig. 8Effect of variation amplitudes for the (TVGB) on the dynamic response of the gear system under the different dynamic transmission error
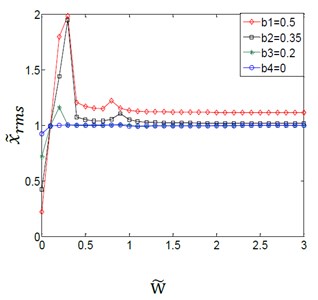
a)0.1
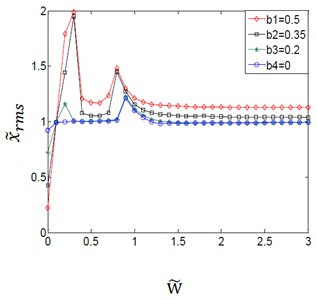
b)0.3
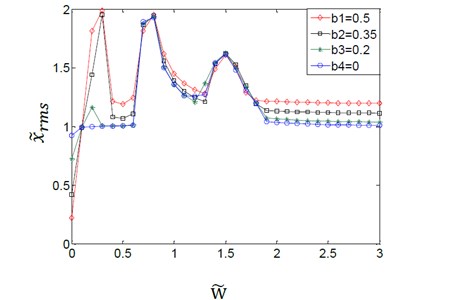
c)0.7
The couple effect between the VAFTGBWTV and the time-varying dynamic transmission error on the gear system is shown in Fig. 8. When the dynamic transmission error variation amplitude is 0.1 as shown in Fig. 8(a), the phenomenon of vibration jump does not appear when the variation amplitude of the gear backlash is assumed to have a value of 0. And the variation amplitudes for the (TVGB) almost have no effect on the gear system except when the speed is very small. When the dynamic transmission error variation amplitude is 0.3 as shown in Fig. 8(b), the effect of the variation amplitudes for the (TVGB) on the gear system is bigger than that when the error is 0.1. The first vibration jumping speed is 0.9 when the variation amplitude of gear backlash is assumed to have a value of 0, and the speed is 0.2 when the value is 0.2, 0.35 or 0.5. When the transmission error variation amplitude is 0.7 as shown in Fig. 8(c), the speed of the first vibration jump is 0.7, and the critical speed of the vibration jumping is smaller than that when the error is 0.3. The numbers of vibration jumps are three times, which is more than that when the error is 0.3. Clearly from these results, the effect of variation amplitudes for the (TVGB) on the gear system tends to increase with increasing dynamic transmission error. With increasing dynamic transmission error, the amplitude, the first speed and the numbers of vibration jumps which affected by the variation amplitudes for the (TVGB) tend to increase.
5. Experimental verification of vibrations characteristic of the gear system under various operating conditions
Vibrations signals are taken from the Qian-Peng experimental platform. Acceleration sensors are placed on the bearing at the output of the gearbox, as shown in Fig. 11. The vibration amplitude is measured using a two-channel Emerson offline monitoring system with a sampling frequency of 2000 Hz and a sampling time of 1 s. Two types of gear pair are selected. And the variation amplitude of gear backlash is assumed to have a value of 0.2 and 0.35 respectively, as shown in Fig. 9 and 10.
Fig. 9The variation amplitude of gear backlash is 0.2

Fig. 10The variation amplitude of gear backlash is 0.35

Fig. 11The gearbox experimental table and Emerson offline monitoring system

5.1. Experimental verification of the effect of the variation amplitudes for the (TVGB) on the gear system under different load
First of all, the acceleration sensor was placed at the gear box bearing seat. The instrument is connected, and the signals are collected, and the collected signals are transmitted to the computer. The data is exported and Matlab software is used to process the corresponding data. By adjusting the brakes at the output of the gear box, different output loads can be obtained. Different speeds can be obtained by adjusting the transmission. When the output load is 0.6, the regulation speed is 0.2 and 0.4 respectively, and the other parameters remain unchanged. In this case, the vibration accelerations of the gearbox collected are shown in Fig. 12(a) and 12(b). When the dimensionless speed is 0.2, all data collected in 1s is computed for root mean square values. And the root mean square values of the gearbox vibration with a dimensionless speed of 0.2 can be obtained. The same method can be used to obtain the root mean square values of the gearbox vibration at other different dimensionless speeds. The dimensionless loads (), which are assumed to have a value of 0.6 and 1.2 respectively, are obtained using Eqs. (17), (18). The two sets of gear systems are put into the gearbox experimental table respectively. With the other parameters hold constant, the vibration amplitudes at the gearbox bearing for various loads are obtained. The experimental and simulated values are shown in Fig. 13.
Fig. 12a) The variation amplitudes of the gearbox bearing under the dimensionless speed is 0.2, b) the variation amplitudes of the gearbox bearing under the dimensionless speed is 0.4
a)
b)
Fig. 13Effect of variation amplitudes for the (TVGB) on the vibration amplitude of the gearbox bearing under different load torques
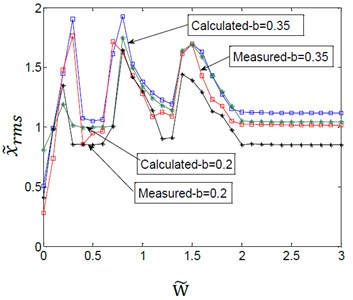
a)0.6
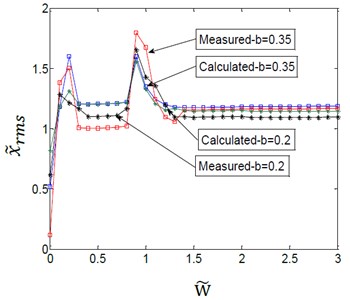
b)1.2
As indicated in Fig. 13, the simulation results of the coupled model were consistent with the experimental analysis results. And the error between the experimental and simulated values was shown in Table 3. The effect of the variation amplitudes for the (TVGB) on the gear system tends to decrease with increasing of the load. It can be seen from Fig. 13(b) that with the load held constant the first speed, the vibration amplitude and the number of vibration jumps increase with increasing of the variation amplitudes for the (TVGB).
Table 3Error between experimental and simulated values
Backlash amplitude | 0.6 | 1.2 | ||
Maximum error | Minimum error | Maximum error | Minimum error | |
0.2 | 0.31 | 0.05 | 0.2 | 0.04 |
0.35 | 0.26 | 0.03 | 0.17 | 0.03 |
5.2. Experimental verification of the effect of the variation amplitudes for the (TVGB) on the gear system under damping ratio
The relation between the damping ratio and lubricant viscosity can be derived using Eqs. (24)-(30). So, the gear system with different damping ratios can be obtained by selecting different viscosity lubricants. With the other parameters held constant, the vibration amplitudes at the gearbox bearing for various damping ratios were obtained. The experimental and simulated values are shown in Fig. 14.
Fig. 14Effect of variation amplitudes for the (TVGB) on the vibration amplitude of the gearbox bearing under different damping ratio
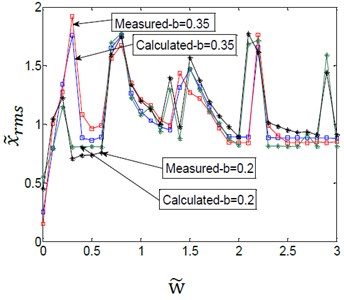
a)0.01
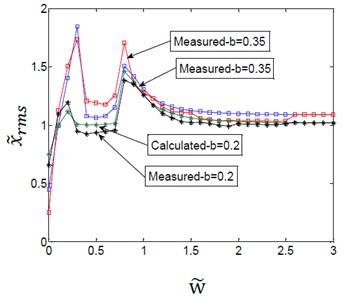
b)0.06
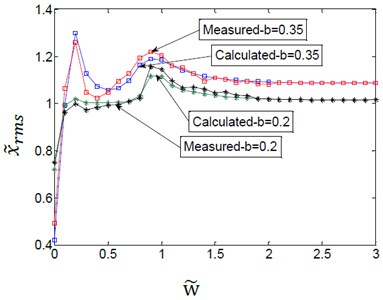
c)0.12
Table 4Error between experimental and simulated values
0.01 | ||
Backlash amplitude | Maximum error | Minimum error |
0.2 | 0.19 | 0.05 |
0.35 | 0.15 | 0.02 |
0.06 | ||
Backlash amplitude | Maximum error | Minimum error |
0.2 | 0.16 | 0 |
0.35 | 0.12 | 0 |
0.12 | ||
Backlash amplitude | Maximum error | Minimum error |
0.2 | 0.11 | 0 |
0.35 | 0.07 | 0 |
As indicated in Fig. 14, the simulation results were consistent with the experimental analysis results. And the error between the experimental and simulated values was shown in Table 4. The effect of the variation amplitudes for the (TVGB) on the gear system tends to decrease with increasing of the damping ratio. It can be seen from Fig. 14(c) that with the damping ratio held constant the first speed, the amplitude and the number of vibration jumps increase with increasing of the variation amplitudes for the (TVGB). The measured vibration amplitudes were slightly greater than the simulated values. The difference may be caused by the various experimental conditions: for various vibration sources are superimposed, resulting in slightly higher measured vibration amplitudes. However, the measurements verified the correctness and the validity of the coupling model.
6. Conclusions
1) A quantitative analysis was conducted on the coupling effects of the variation amplitudes for the (TVGB) and the different parameters on the gear system were considered simultaneously. Both the simulation model and measurements taken from a gearbox experimental table showed increasing the load, the torques, damping ratio, system parameter or decreasing the directional rotation radius variation or dynamic transmission error caused the effect of the variation amplitudes for the (TVGB) (the vibration amplitude, the first speed and the number of vibration jumps) on the gear system to gradually decrease.
2) The modified coupling model, which improved the original model assuming that the backlash value was constant, was developed to study the effect of variation amplitudes for the (TVGB) on the vibration amplitude of gear system under various mesh parameters. A method for solving gear meshing stiffness based on the energy method was formulated in the coupling model, improved the traditional model based on the Fourier expansion to solve the meshing stiffness of the gear system, making the solution results closer to the meshing stiffness of the actual gear system meshing process. At the same time, a nonlinear damping calculation method is applied to solve the damping of gear system.
3) Test data from an actual gearbox verified the model accuracy. The model was shown to be capable of simulating the mutually coupled effect between the different variation amplitudes of the gear backlash with time-varying and the different parameters on the gear system. In particular, from these results, we can obtain an appropriate value of the gear backlash which has a minimum impact on the gear system. In this way, the bigger vibration value of the gearbox caused by the improper gear backlash can be avoided.
References
-
Guerine Ei Hami A. A. Dynamic response of a spur gear system with uncertain friction coefficient. Advance in Engineering Software, 2016, https://doi.org/10.1016/j.advengsoft.2016.05.009.
-
Wang J. G., He G. Y., Zhang A. J. Nonlinear dynamics analysis of the spur gear system for railway locomotive. Mechanical Systems and Signal Processing, Vol. 85, 2017, p. 41-55.
-
Cho J. R., Jeong K. Y., Park M. H. Dynamic response analysis of wind turbine gearbox using simplified local tooth stiffness of internal gear system. Journal of Computational and Nonlinear Dynamics, Vol. 12, Issue 3, 2016, p. 34502.
-
Wang X. F., Li Z. R., Zhu W. D. Dynamic analysis of a geared infinitely variable transmission. Journal of Computational and Nonlinear Dynamics, Vol. 10, 2016, p. 21013.
-
Liu X. Z., Yang Y. H., Zhang J. Investigation on coupling effects between surface wear and dynamics in a spur gear system. Tribology International, Vol. 101, 2016, p. 383-394.
-
Wei S., Zhao J. S., Han Q. K. Dynamic response analysis on torsional vibrations of wind turbine geared transmission system with uncertainty. Renewable Energy, Vol. 78, 2015, p. 60-67.
-
Saghafi A. An analytical study of controlling chaotic dynamics in a spur gear system. Mechanism and Machine Theory, Vol. 96, 2016, p. 179-191.
-
Chen S. Y., Tang J. Y. Nonlinear dynamic characteristics of geared rotor bearing systems with dynamic backlash and friction. Mechanism and Machine Theory, Vol. 46, 2011, p. 466-478.
-
Moradi H., Salarieh H. Analysis of nonlinear oscillations in spur gear pairs with approximated modeling of backlash nonlinearity. Mechanism and Machine Theory, Vol. 51, 2012, p. 14-31.
-
Sun T., Hu H. Y. Nonlinear dynamics of a planetary gear system with multiple clearances. Mechanism and Machine Theory, Vol. 38, 2003, p. 1371-1390.
-
Jinyuan C. S. T. Effect of backlash on dynamics of spur gear pair system with friction and time-varying stiffness. Journal of Mechanical Engineering, Vol. 45, Issue 8, 2009, p. 022.
-
Chen Q., Ma Y. B. Research on gears dynamic performance influenced by gear backlash based on fractal theory. Applied Surface Science, Vol. 313, 2014, p. 325-332.
-
Wang J., Lim T. C., Li M. F. Dynamics of a hypoid gear pair considering the effects of time-varying mesh parameters and backlash nonlinearity. Journal of Sound and Vibration, Vol. 308, 2007, p. 302-329.
-
Dareing D. W., Johnson K. L. Fluid film damping of rolling contact vibrations. Journal of Mechanical Engineering Science, Vol. 17, 1975, p. 214-218.
-
Sabot J., Krempf P., Janolin C. Non-linear vibrations of a sphere–plane contact excited by a normal load. Journal of Sound and Vibration, Vol. 214, 1998, p. 359-375.
-
Tian X. H. Dynamic Simulation for System Response of Gearbox Including Localized Gear Faults. Department of Mechanical Engineering, University of Alberta.
-
Chen Z. G., Shao Y. M. Dynamic simulation of spur gear with tooth root crack propagating along tooth width and crack depth. Engineering Failure Analysis, Vol. 18, Issue 8, 2011, p. 2149-2164.
Cited by
About this article
The work was financially supported by the Natural Science Foundation of China (Grant No. 51575007 and No. 51375020).
