Propagation of rotational waves in a block geomedium

1. Introduction

The classical theory of elasticity is based on idea that solid is a continuum of material points possessing only translational degrees of freedom. However, phenomena are frequently observed in the nature, which can be explained by the rotational dynamics of individual particles of a medium, independently on the absolute particle size [1-4]. Consideration of solids with internal degrees of freedom led to the construction of the Cosserat, Mindlin-Eringen, Leroux continual-phenomenological models, as well as other generalized continua [3-5]. At present, structural models are developed for advanced materials with micro- and nanostructure [6-10].

On the other hand, recent data of geological and geophysical research argue that the Earth’s crust consists of non-point particles-blocks that are able to rotate. Thus, according to [2, 11], the state of the Earth’s crust is determined by the “inner motion potentialz’ [12] and “self-energy” [13]. Within the scope of the mechanical concept, motion with such properties [11, 12] can occur only under the influence of own angular momentums of the blocks, in fact, their spins [14]. Interaction of the blocks determines both the motion of the Earth’s crust as a whole and its “volume flowing in the cold state” [15] and / or its rheidity properties [16]. The Earth’s rotation around its axis with angular velocity $\mathrm{\Omega }$ and the rotational movements of crust blocks provided by “own moments” $J\mathrm{\Omega }$, where $J$ is the moment of inertia of the spherical block, play an important role in geodynamics.

So, geophysical observations made during a long time interval enabled one, for example, to formulate a conclusion that Easter Island (300×400 km²) in the Pacific Ocean for 5 million years (it is time of its existence) has turned almost by 90° [17] that corresponds to the angular velocity 0.5$\pi$ rad/5·10⁶ years ≈ 3·10^-7 rad/year. Moreover, Siberian platform performs a rather complex motion as a rigid plate. In the period 2.5-1 billion years ago it was located, mainly, in the equatorial and low northern latitudes, performing quasi-oscillation rotations relative to the meridian with amplitude up to 45°, whereas in the period 1.6-1 billion years ago it turned counterclockwise at the angle of about 90° [18].

On the basis of these data, A. V. Vikulin with his co-authors developed a “rotational” approach to solving geodynamic problems (see, for example, [16, 19]). This approach is based on the following assumptions: an elementary part of the rotating solid body – the Earth’s crust block – is, first of all, a rigid non-deformable volume; secondly, its motion occurs under the action of its own moment; thirdly, such a motion leads to change of the stress state of the crust surrounding the block [16]. Within the framework of this rotational model it is possible to describe the whole range of geodynamic velocities of rotational waves that are typical both for geophysical and geological processes – from slow rotational waves characterizing redistribution of tectonic stresses up to fast seismic waves [16, 20, 21]. Further, in accordance with this approach, we shall consider motion of two interacting crust blocks in a geomedium rotating with angular velocity $\mathrm{\Omega }$.

2. Rotational movements of crust blocks

The interaction energy of two crust blocks located at a distance of $l$ from each other and possessing radiuses $R_{01}$ and $R_{02}$ is calculated by the equation [20]:

where $\phi$ is the angle between the moments of the blocks. Due to this energy, each block tends to turn the other block. The torque caused by the interaction of blocks is determined by deriving Eq. (1) with respect to angle $\phi$:

The torque Eq. (2) is applied to the surface of each of the blocks from the side of elastic field and is directed by such a way in order to decrease their interaction energy. This torque has the same magnitude for both blocks, but it is directed in opposite sides for different blocks. In this case, the angles of rotation of the blocks – the centers of earthquakes [16] – are equal to 10^-4-10^-2 rad. It means that, if earthquakes occur in one place every 100-1000 years, the angular velocity equals 10^-7-10^-4 rad.

Rotational movements of a block generating its own elastic field and, in accordance with Eqs. (1) and (2), interacting with their own elastic fields of other equally large blocks of the chain are described by sine-Gordon equation in the dimensionless form [16]:

However, a case of a chain with heterogeneous rotations of blocks taking into account the friction forces along their borders is more appropriate to the real geodynamic process [16]. It should be noted that the friction is regarded as the dissipation factor preventing the rotational interaction of the blocks. In this case, the rotational motions of crust blocks are described by the sine-Gordon equation with dissipation:

where $\mu$ is a dissipation factor. For definiteness, we take $\mu >0$ (the positive $\mu$ has a physical meaning in relation to the Earth’s crust).

3. Dispersion properties of sine-Gordon equation with attenuation

In order to analyze dispersion properties of Eq. (4), first, we shall linearize it:

If to search a solution of Eq. (5) in the form of a traveling harmonic wave $\phi \left(x,t\right)={\phi }_0\mathrm{e}\mathrm{x}\mathrm{p}\left(i\left(\omega t-kx\right)\right)$, one can find the following dispersion equation:

From this equation, it follows that the wavenumber is complex:

The complex wavenumber means that the wave has a propagation constant and decays exponentially, i.e. displacement can be written as:

Substituting Eq. (7) into the complex Eq. (6) and separating the real and imaginary parts, one can obtain a set of algebraic equations:

From Eq. (8) it is possible to obtain the expressions for the real $k_1$ and imaginary $k_2$ parts of the wave number:

where, for brevity, the notation $m={\left({\omega }^2+{\omega }_0^2\right)}^2+{\mu }^2{\omega }^2$ is entered. Further investigations are carried out for couple:

From the analysis of Eqs. (9) and (10) (Fig. 1) it follows that high-frequency perturbations ($\omega \to +\infty$) propagate actually without dispersion ($k_1=\omega /c$), whereas the dissipation takes the constant value $k_2=-\mu /2c$, which does not depend on the frequency. If there is no dissipation, the imaginary part is absent too, whereas the real part of the dispersion curve has a cut-off of the wave number $k_1={\omega }_0/c$. The low-frequency perturbations possess a frequency-dependent dissipation and a dispersion.

Fig. 1 shows that the curve of propagation, $k_1\left(\omega \right)$, changes its convexity (concavity), when $\mu =2\sqrt{3}{\omega }_0$. If $0<\mu <2\sqrt{3}{\omega }_0$, the curve $k_1\left(\omega \right)$ is concave for all the frequencies, and if $\mu >2\sqrt{3}{\omega }_0$, then the curve has some intervals of convexity. The attenuation curve $k_2$ decreases and it is concave in the whole range of frequencies for all values of the dissipation factor. Dependences of attenuation factor $\alpha =\frac{Im\left(k\right)}{Re\left(k\right)}=\frac{k_2}{k_1}=\frac{1}{\mu \omega }\left({\omega }^2+{\omega }_0^2-\sqrt{m}\right)$ on frequency are also plotted in Fig. 1 for different values of dissipation factor $\mu$. The attenuation factor decreases in the range of low frequencies and grows at higher frequencies. The graph has minimum points at $\omega =\pm {\omega }_0$ and changes its convexity.

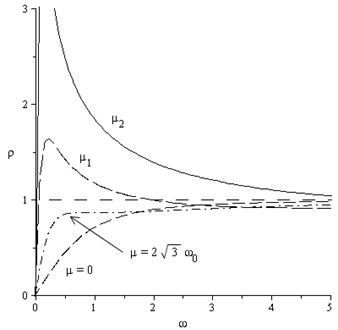
The density of the spectral frequency distribution, $\rho \left(\omega \right)$, is directly proportional to [22]:

The function graph $\rho \left(\omega \right)$ has a horizontal asymptote $\rho =1/c$ for $\omega \to +\infty$ (Fig. 2). Fig. 2 also shows that the low-frequency excitations exhibit dispersion only for $\mu >2\sqrt{3}{\omega }_0$. When the dissipation factor grows up till $2\sqrt{3}{\omega }_0$, function $\rho \left(\omega \right)$ becomes monotonically increasing throughout the interval and its graph varies within the curves shown in Fig. 2 (dotted and dash-dot lines). A sharp jump of the density of the spectral distribution is not observed. If $\mu$ exceeds $2\sqrt{3}{\omega }_0$, function $\rho \left(\omega \right)$ becomes non-monotonic, there appear a maximum in its graph near zero. For large values of the dissipation factor, a clear break of the curve $\rho \left(\omega \right)$ is visible at the origin, i.e. the frequency spectrum becomes continuous for $\omega =0$. Thus, it is obviously that the low-frequency perturbations have a dispersion, when $\mu >2\sqrt{3}{\omega }_0$. The more is $\mu$, the stronger is the dispersion at low frequencies.

Fig. 1Dependences of k1ω, k2ω, and αω for a) 0<μ<23ω0 and b) for μ>23ω0

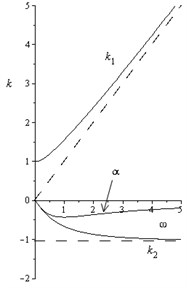
a)

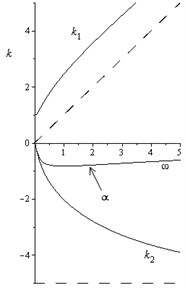
b)

Fig. 2Dependences ρω for different values of μ, 23ω0<μ1<μ2

For studying the energy transfer process as well as the wave field structure apart from the excitation source, the propagating modes corresponding to the real areas of dispersion curves are of primary importance. The phase velocity $v_{ph}=\omega /k_1$ is the most accessible for researching the characteristics of propagating modes. If to divide the first Eq. (9) by $\omega$ and to overturn the resulting fraction, it is possible to obtain an expression for the phase velocity:

The group velocity is defined by equation $v_{gr}=d\omega /d{k}_1$. Deriving the expression for the real part of the wave number with respect to $\omega$ and overturning the received fraction, one can obtain an expression for the group velocity:

where, as before, $\sqrt{m}={\omega }^2\sqrt{{\left(1+{\omega }_0^2/{\omega }^2\right)}^2+{\mu }^2/{\omega }^2}$.

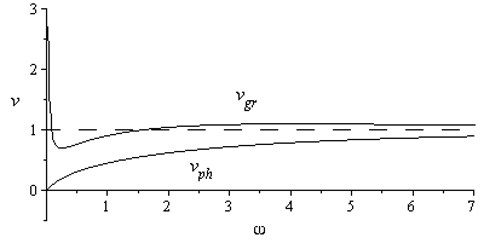
Dependences of the phase and group velocities for various values of the dissipation factor are shown in Fig. 3. Graph of functions Eqs. (11) and (12) have a common horizontal asymptote: $v_{ph}=v_{gr}=c$. For great values of $\mu$ ($\mu \to +\infty$), the group velocity curve is close to $v_{gr}=2\sqrt{2}c\sqrt{\omega /\mu }$. For all values of the dissipation factor $v_{gr}>v_{ph}>0$, i.e. the dispersion is anomalous in the entire frequency range.

Fig. 3Dependences vphω and vgrω for μ1 a) and μ2 b), μ1<μ2

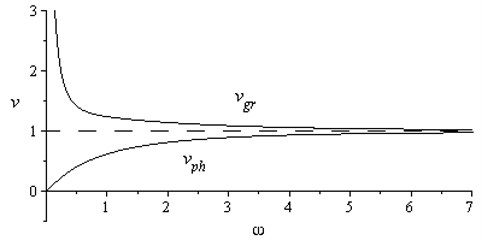
a)

b)

Thus, from the analysis of the dependence Eq. (12) it follows that for $\mu >0$ the linear waves propagate with velocities $v_{ph}<c$, i.e. the linear wave velocities are bounded above.

4. Stationary waves in a block geomedium

Let us consider a solution of Eq. (4) in the form of stationary waves that propagate with a constant velocity and do not change their shape. In solutions of this type, the coordinate and time are included in combinations $\xi =x-vt$, where $v=const$ is the nonlinear wave velocity. If to make substitution $u=\phi \left(\xi \right)$ in Eq. (4), it is possible to pass from the partial differential equation to the ordinary differential equation:

where the primes denote derivatives with respect to $\xi$.

Since the velocities of linear and nonlinear waves are different [23], one can conclude that the velocities of nonlinear waves are bounded below, i.e. $v^2>c^2$ and Eq. (13) takes on the form:

where $W\left(u\right)$ is the potential energy and $\frac{dW}{du}=-\frac{{\omega }_0^2}{v^2-c^2}\mathrm{s}\mathrm{i}\mathrm{n}u$. Eq. (14) represents an equation of a nonlinear oscillator with damping. The oscillator starts to move from the unstable equilibrium state, where the potential energy has the maximum value $W=$ 0. The potential energy of the oscillator has the minimum value $W=-2{\omega }_0^2/\left(v^2-c^2\right)$ at a position that corresponds to a stable equilibrium state. The oscillator potential energy takes on the form:

Function (15) has extrema in points determined by the equation $dW/du=0$: $u=\pi k$, $k\in \mathbf{Z}$. The oscillator has two different equilibrium states: $u_1=2\pi k$, $k\in \mathbf{Z}$ and $u_2=\pi +2\pi k$, $k\in \mathbf{Z}$. Let us investigate stability of the equilibrium states.

1) We define small deviations from the equilibrium states $u_2=\pi +2\pi k$$\text{(}k\in \mathbf{Z}\text{)}$: $u=u_2+\tilde{u}=\pi +\tilde{u}$, where $\tilde{u}\to \pm 0$. After substitution of these expressions into Eq. (14) we shall linearize the obtained equation:

If to search a solution in the form $\tilde{u}=\mathrm{e}\mathrm{x}\mathrm{p}\left(\lambda \xi \right)$, one can obtain a characteristic equation:

Its roots have the form:

If ${\left(\mu v\right)}^2>4{\omega }_0^2\left(v^2-c^2\right)$, then the roots ${\lambda }_1$ and ${\lambda }_2$ are real and of the same sign (positive), hence, the equilibrium state $u_2=\pi +2\pi k\text{,}$$k\in \mathbf{Z}$ is an unstable node (Fig. 4). When ${\left(\mu v\right)}^2<4{\omega }_0^2\left(v^2-c^2\right)$, the roots are complex with a positive real part, therefore, the considered equilibrium state is an unstable focus (Fig. 5).

2) Let us now consider the equilibrium states $u_1=2\pi k$ ($k\in \mathbf{Z}$). If to put $u=u_1+\tilde{u}=\tilde{u}$, where $\tilde{u}\to \pm 0$, then linearization of Eq. (6) yields the following equation:

After substitution of $\tilde{u}=\mathrm{e}\mathrm{x}\mathrm{p}\left(\lambda \xi \right)$ one can receive a characteristic equation with the corresponding roots:

Since $v^2>c^2$, roots ${\lambda }_1$ and ${\lambda }_2$ are real and of opposite signs. Hence, the equilibrium state $u_1=2\pi k$, $k\in \mathbf{Z}$ is a saddle (Figs. 4, 5).

Fig. 4Phase portrait for 2ω0/μ21-c/v2<1

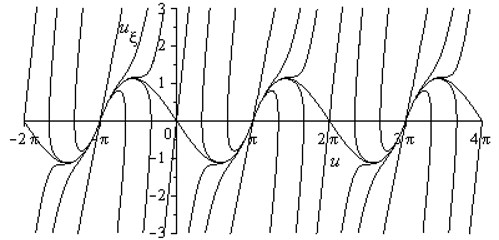
The oscillator starts to move from the unstable equilibrium state $u_2$ (node, focus) at $\xi \to -\infty$ and approaches to the saddle point $u_1$ at $\xi \to +\infty$ (Figs. 4, 5).

Fig. 5Phase portrait for 2ω0/μ21-c/v2>1, separatrix for μ= 0

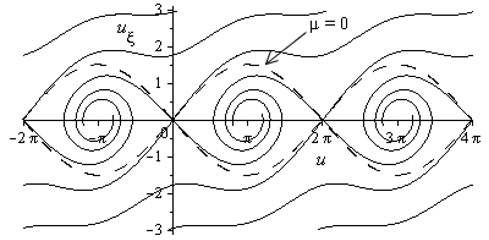
Solutions of Eq. (13) are shock waves. If ${\left(\mu v\right)}^2>4{\omega }_0^2\left(v^2-c^2\right)$, the solution is a stationary shock wave [23] of small amplitude (Fig. 3, a dotted line). It has the form of a monotonic difference between two constant values $u_1=0$ and $u_2=\pi$. When ${\left(\mu v\right)}^2<4{\omega }_0^2\left(v^2-c^2\right)$, the solution is a stationary shock wave with an oscillating leading edge (Fig. 6, a firm line). At the trailing edge, the solution has the form of exponentially growing harmonic oscillations.

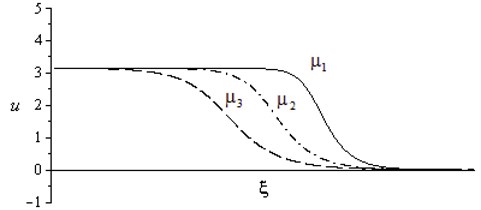
The profile of the stationary shock wave is shown in Fig. 7 for different values of the dissipation factor $\mu$. From this Fig. 7 it is visible that growing of the dissipation factor $\mu$ leads to increasing of the length of wave difference $\delta$. Increasing of the nonlinear wave velocity $v$ also contributes to growing of the length of wave difference. However, increasing of the nonlinearity degree of Eq. (13) leads to growing of the steepness of the shock wave front, i.e. to decreasing of the length of wave difference. The characteristic length of the difference $\delta ~\mu v/{\omega }_0^2$ is directly proportional to the wave velocity and attenuation. But increasing of the nonlinear effects leads, vice-versa, to decreasing of $\delta$.

Fig. 6The profile of the stationary shock wave 2ω0/μ21-c/v2<1 (curve 1), 2ω0/μ21-c/v2>1 (curve 2)

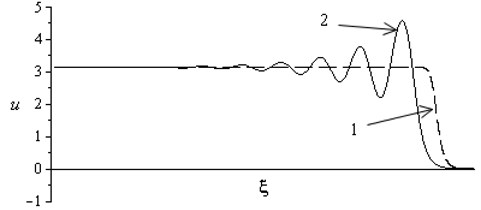
Fig. 7The profile of the stationary shock wave for various values of the dissipation factor μ, μ1<μ2<μ3

5. Conclusions

In this paper, it is assumed that the rotational movement of crust blocks and the corresponding rotational waves characterizing redistribution of tectonic stresses are described by the sine-Gordon equation [16, 21]. However, a case of a chain with heterogeneous rotations of blocks taking into account the friction forces along their borders is more appropriate to the real geodynamic process. In this case, the friction is considered as a dissipation factor, which, on account of frictional forces between blocks of a geomedium, prevents their rotational interaction [16]. As a result, the movement of a chain of crust blocks is described by the modified sine-Gordon equation containing a dissipative term. The dispersion properties of this equation have been analyzed. The presence of anomalous dispersion has been revealed for all values of the dissipation factor. It is shown that the dispersion is manifested in the low-frequency range at high values of the dissipation factor, and the greater is the dissipation factor, the larger is the dispersion at low frequencies. The features of propagation of the stationary shock (seismic) wave in a geomedium with account of dissipation have been investigated. It has been found that the shock wave front width is directly proportional to the nonlinear wave velocity and to the dissipation factor of the medium, but it is inversely proportional to the nonlinearity coefficient. The obtained research results can be used for the study of geodynamic processes in various fields of the Earth and for improvement of earthquake forecasting methods.