Macroscopic and microscopic simulation of silo granular flow based on improved multi-element model

Feng, Yong; Yuan, Ziran

doi:10.21595/jve.2019.20558

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 June 2019

Check for updates

Macroscopic and microscopic simulation of silo granular flow based on improved multi-element model

Yong Feng¹

Ziran Yuan²

^{1, 2}Henan University of Technology, Zhengzhou, China

Corresponding Author:

Ziran Yuan

Cite the article Download PDF

Abstract

In the PFC simulation of silo granular discharge, spherical particles were used in the traditional model, which could not accurately reflect macroscopic and mesoscopic mechanism during discharge of wheat, rice and other particles with non-spherical shapes. This research provides an improved multi-element model consisting of clump elements and ball elements. The model uses clump elements to simulate non-spherical grain particles and ball elements to simulate dust particles. The numerical simulation was carried out with the improved multi-element model, and the results are compared with the traditional simulation which uses the spherical ball elements and the experiment of grain discharge. It demonstrates that: (1) In terms of the normal wall pressure, the dynamic pressure fluctuation in flow with improved multi-element model is more gradual, and the discharge process lasts longer, the normal pressure simulation results are more accurate than the traditional model. (2) In terms of the meso-structure of the granular material, compared with traditional spherical ball model, the material packing porosity of the improved multi-element model decreases and the coordination number increases, which is denser and in consistent with the actual situation. (3) Particle shape would affect the meso-mechanical behavior of particles. The simulation results demonstrate that, compared with the traditional spherical ball model, the contact forces in the improved multi-element model increases, and the distribution of contact force chains is more uniform and denser; several arching force chains could be clearly seen in the improved multi-element model, which clearly reflects the dynamic change law of the instantaneous arch. The improved multi-element model established in this paper further improves the accuracy of simulation and reflects the dynamic changes of the normal pressure on the silo wall, granular material structure and meso-mechanical parameters during grain discharge.

Macroscopic and microscopic simulation of silo granular flow based on improved multi-element model

Highlights

An improved multi-element model is proposed to simulate the non-spherical particles and the dust contained in the material.
The contact models between particles and walls are derived for the linear contact model, and the force-displacement update formula is established.
Satisfactory results are obtained in simulation, and compare the results of the multi-element model and the traditional spherical ball model.

1. Introduction

Flow of granular materials in silos is important in many process engineering applications such as food, agricultural, and powder industries. The ﬂow behaviors of these granular materials are generally difficult to be predicted on account of the complex properties of granular materials [1, 2]. The comprehension of the ﬂow behaviors for non-spherical granular materials in the silo is important to the design and application of silos.

Since CUNDALL put forward the discrete element method, PFC, DEM and other numerical simulation software based on the discrete element method have been widely used in the field of granular materials research [3-5]. But most research focus on the spherical materials, the ball element in PFC is often used to simulate grain particles in silos [6-8]. However, there is significant deviation between macro-mechanical simulation and experimental results, and the meso-mechanical parameters of the particles are not comprehensive [9, 10]. An important reason for the above deviation is that, grain particles under natural conditions would not exist in a spherical shape [11, 12]. Furth more, the traditional spherical ball model cannot reflect the differences of non-spherical grain materials, such as wheat and paddy, and the influence of dust-containing rate on the discharge process. Therefore, it is difficult to accurately reflect the macroscopic and mesoscopic mechanical mechanism of grain flow in silos.

Some researchers have proposed clump element to simulate corn-shaped particles, disc-like particles and others [13, 14]. They indicate that the discrete element method is a powerful tool to analyze the interactions between irregularly shaped particles. Particle shape has a significant effect on the discharge rate, and particle interlocking might influence flow behavior in silos [15, 16]. However, in previous work, there is no quantitative study on the effect of grain shape and dust content, the accuracy of macro parameters suck as wall pressure in flow is not studied enough, and the mesoscopic mechanism studied in previous work are not comprehensive enough. In addition, the range of deviations in the case of non-spherical materials such as wheat-shaped particles in flow is unknown. The mesoscopic simulation results such as packing porosity, the coordination number and the dynamic force chains were examined and compared with the experiment result in the literature. This paper provided more comprehensive quantification and analysis.

Based on the above analysis, an improved multi-element model consisting of clump elements and ball elements is proposed in this paper. The model would use clump elements to simulate irregular grain particles [17, 18] and small ball elements to simulate dust particles. On the basis of deducing the contact constitutive relation in particles, between particles and environment [19-21]. The numerical simulation with the improved multi-element model was carried out based on the experiment of grain discharge, and the simulation results of improved model were compared with the traditional spherical ball model.

The current work focuses to establish an improved multi-element model for non-spherical grain particles such as wheat and paddy, to simulate the effects of grain morphology and dust content on the macroscopic and mesoscopic mechanical parameters during discharge, to reveal the macroscopic and mesoscopic mechanical mechanism objectively and accurately and provide a reference for the numerical simulation of irregular grain. In the field of engineering application, the improved model could be used to simulate and predict the wall pressure of silos and provide guidance for silo design.

2. Experiment test

The model is made according to the actual common silos reasonable size of the scale 20:1. The height of the experimental silo is 1000mm, the radius of silo is 250 mm, the wall thickness is 5 mm, and the half angle of the hopper part is 60°. The strain gauge is arranged at each monitoring points of the silo cylinder wall, to detect the normal pressure of the silo cylinder part during discharge. The geometry of the silo model and the arrangement of monitoring points are shown in Fig. 1. The experimental model is shown in Fig. 2. The model silo was filled with wheat, diameters ranging from 5 mm to 6 mm, and the orifice plate would be removed for discharge after filling and store for two days.

Fig. 1Silo model geometry and monitoring points arrangement

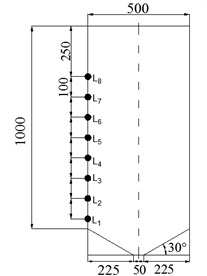
Fig. 2Grain discharge test system

3. Numerical models

3.1. Improved multi-element model

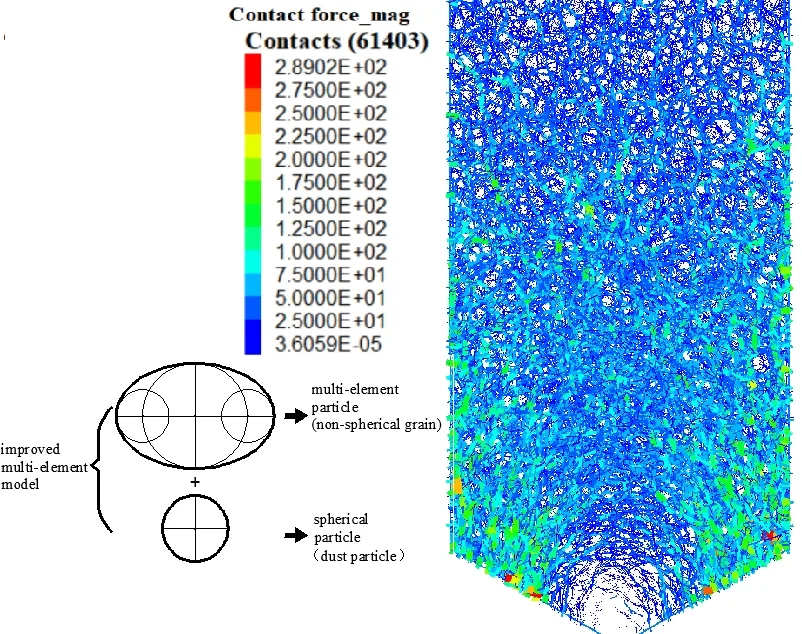
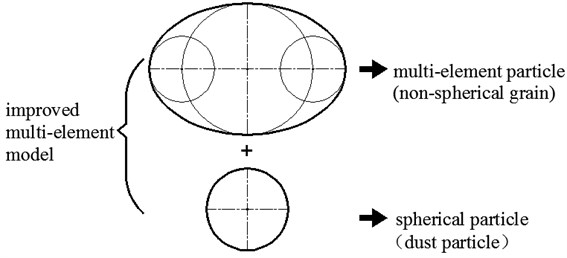
The improved multi-elements model proposed in this paper consists of clump elements and small ball elements. The model would use multi-elements to simulate non-spherical grain particles, and use small ball elements to simulate dust particles. Multi-element particles would simulate the non-spherical particles with “clump”, which consists of three rigid spheres overlapping with each other. This research focus on the shape of non-spherical grain particles (such as wheat, rice), and the improved multi-element model system is shown in Fig. 3.

Fig. 3Improved multi-element model system

3.2. Contact model

The recent research demonstrates that linear contact model is widely used in PFC simulation in the granular flow [22-24], the contact models between particles and walls are derived respectively for the numerical simulation, and the force-displacement update formula is established, which is described in this section.

3.2.1. Contact between particles

1. Multi-element particles.

The multi-element particle is simplified as an ellipse. According to the force-displacement law and the calculation method in simulation [25, 26], the unit vector model and the contact deformation of two particles could be obtained. Two elliptical particles are in contact with each other as shown in Fig. 4, and it is considered that the normal and the tangential vector of particles at the contact point is:

1

\vec{n} = (n_{x}, n_{y}),

2

\vec{t} = (t_{x}, t_{y}) .

Fig. 4Contact between multi-element particles

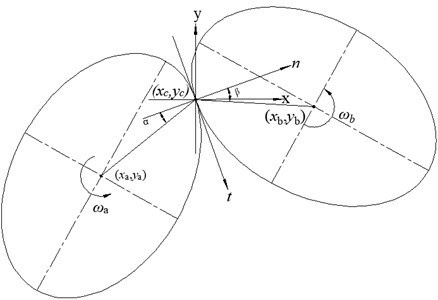
According to the geometrical meaning of ellipse, the radius vector of ellipse $\vec{r_{a}}$ , $\vec{r_{b}}$ and the angle between the normal vector are $α$ and $β$ , respectively. The center coordinates of the particles are $(x_{a}, y {}_{a})$ $(x_{b}, y {}_{b})$ respectively, and where $\vec{v_{a}}$ , $\vec{v_{b}}$ is the velocity of the particles’ centers. The velocity of two particles is expressed as Eqs. (3) and (4) at the contact point:

3

\vec{v_{c a}} = \vec{v_{a}} + \vec{w_{a}} \times \vec{r_{a}},

4

\vec{v_{c b}} = \vec{v_{b}} + \vec{w_{b}} \times \vec{r_{b}} .

The relative velocity at the contact point of the two particles is Eqs. (5) and (6):

5

\vec{d v_{c}} = \vec{v_{c a}} - \vec{v_{c b}},

6

\vec{d v_{c}} = \vec{v_{a}} + \vec{w_{a}} \times \vec{r_{a}} - (\vec{v_{b}} + \vec{w_{b}} \times \vec{r_{b}}) .

The component relative velocity in the normal and the tangential directions is defined as Eqs. (7) and (8) respectively:

7

\vec{d v_{n}} = (\vec{v_{a}} - \vec{v_{b}}) \vec{n} + (\vec{w_{a}} \times \vec{r_{a}} s i n α - \vec{w_{b}} \times \vec{r_{b}} s i n β),

8

\vec{d v_{t}} = (\vec{v_{a}} - \vec{v_{b}}) \vec{t} + (\vec{w_{a}} \times \vec{r_{a}} c o s α - \vec{w_{b}} \times \vec{r_{b}} c o s β) .

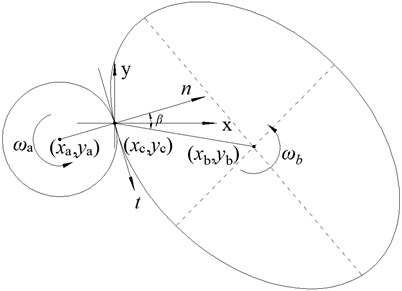
2. Multi-element particle and spherical particle.

Multi-element particle and spherical particle contact with each other (Fig. 5), the center coordinates of the spherical particle $a$ is $(x_{a}, y_{a})$ , the center coordinates of the ellipse particle $b$ is $(x_{b}, y_{b})$ , and the angle between the radius vector of ellipse center and the normal vector $\vec{n}$ at the contact point is $β$ . The velocity of particles $a$ , $b$ are defined as $\vec{v_{a}}$ , $\vec{v_{b}}$ , where the velocity of two particles and the relative velocity of the two particles at the contact points expressed with reference to the contact between two multi-element particles. The relative velocity is Eq. (9):

9

\vec{d v_{c}} = (\vec{v_{a}} - \vec{v_{b}}) + (\vec{w_{a}} \times \vec{r_{a}} - \vec{w_{b}} \times \vec{r_{b}}) .

The component relative velocity in the normal and the tangential directions is calculated as Eqs. (10) and (11) respectively:

10

\vec{d v_{n}} = (\vec{v_{a}} - \vec{v_{b}}) \vec{n} - \vec{w_{b}} \times \vec{r_{b}} s i n β,

11

\vec{d v_{t}} = (\vec{v_{a}} - \vec{v_{b}}) \vec{t} + \vec{w_{a}} \times \vec{r_{a}} - \vec{w_{b}} \times \vec{r_{b}} c o s β .

Fig. 5Contact between multi-element particle and spherical particle

3. Spherical particles.

The mesoscopic state of the two spherical particles, which contact with each other as shown in Fig. 6, and the center coordinates of the two particles are $(x_{a}, y_{a})$ , $(x_{b}, y_{b})$ , $\vec{r}$ is the radius vector of two particles and the central velocity of the spherical particles are defined as $\vec{v_{a}}$ , $\vec{v_{b}}$ respectively. The velocity of two particles at the contact point is expressed with reference as mentioned, the relative velocity of the two particles at the contact point is Eq. (12):

12

\vec{d v_{c}} = (\vec{v_{a}} - \vec{v_{b}}) + (\vec{w_{a}} \times \vec{r} - \vec{w_{b}} \times \vec{r}) .

Fig. 6Contact between spherical particles

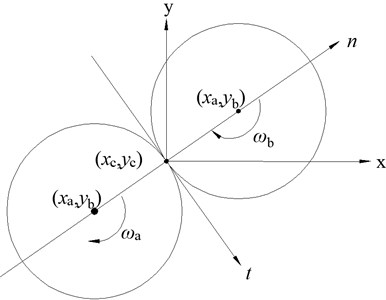
The component relative velocity in the normal and the tangential directions is calculated as Eqs. (13) and (14) respectively:

13

\vec{d v_{n}} = \vec{d v_{c}} \vec{n} = (\vec{v_{a}} - \vec{v_{b}}) \vec{n},

14

\vec{d v_{t}} = \vec{d v_{c}} \vec{t} = (\vec{v_{a}} - \vec{v_{b}}) \vec{t} + (\vec{w_{a}} \times \vec{r} - \vec{w_{b}} \times \vec{r_{}}) .

3.2.2. Contact between particle and wall

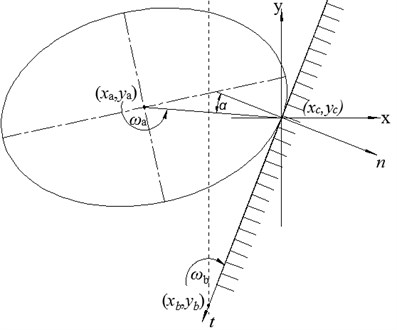
The wall, which defined as b, rotate around the point $(x_{b}, y_{b})$ , particle is defined as a and the center coordinate of the particle is $(x_{a}, y_{a})$ . The coordinates of the contact point between the wall and the particle is $(x_{c}, y_{c})$ . The normal and tangential vectors at the contact point are $\vec{n} = (n_{x}, n_{y})$ , $\vec{t} = (t_{x}, t_{y})$ . The $\vec{v_{a}}$ , $\vec{v_{b}}$ are the velocity of the particle and the wall. The wall would not translate, so the translate velocity of the wall $\vec{v_{b}}$ is zero, where $w_{b}$ is the angular velocity of the wall rotation. Where $\vec{r_{w}}$ is the vector from $(x_{b}, y_{b})$ to the contact point $(x_{c}, y_{c})$ .

1. Multi-element particle and wall.

Fig. 7 is the schematic diagram of multi-element particle in contact with the wall. The velocity of particle and wall is calculated as Eqs. (15) and (16), the relative velocity at the contact point is Eq. (17):

15

\vec{v_{c a}} = \vec{v_{a}} + \vec{w_{a}} \times \vec{r_{a}},

16

\vec{v_{c b}} = \vec{w_{b}} \times \vec{r_{w}},

17

\vec{d v_{c}} = \vec{v_{a}} + (\vec{w_{a}} \times \vec{r_{a}} - \vec{w_{b}} \times \vec{r_{w}}) .

Fig. 7Contact between wall and multi-element particle

The component relative velocity is defined in the normal and tangential directions as follows:

18

\vec{d v_{n}} = \vec{d v_{c}} \vec{n} = \vec{v_{a}} \vec{n} - \vec{w_{a}} \times \vec{r_{a}} \cdot s i n α + \vec{w_{b}} \times \vec{r_{w}},

19

\vec{d v_{t}} = \vec{d v_{c}} \vec{t} = \vec{v_{a}} \vec{t} - \vec{w_{a}} \times \vec{r_{a}} \cdot c o s α .

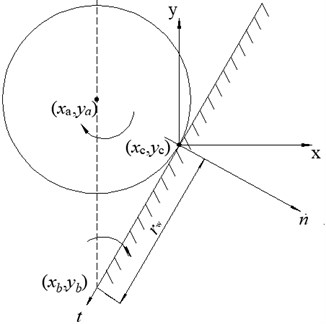
2. Spherical particle and wall.

The velocity expression of particle “ $a$ ” and wall “ $b$ ” at the contact point is similar to that of multi-element and wall. The relative velocity is defined in the normal and the tangential directions as follows:

20

\vec{d v_{c n}} = \vec{d v_{c}} \vec{n} = \vec{v_{a}} \vec{n} + \vec{w_{b}} \times \vec{r_{w}} \vec{n},

21

\vec{d v_{c t}} = \vec{d v_{c}} \vec{t} = \vec{v_{a}} \vec{t} + \vec{w_{a}} \times \vec{r} \vec{t} .

Fig. 8Contact between wall and spherical particle

3.3. Equations of particle motion

The normal and the tangential displacement of particles and walls would generate by the velocity component in the corresponding direction [27, 28], we could obtain the displacement component Eqs. (22) and (23), the displacement would change in a period time according to the velocity component calculated by the above mentioned:

22

\vec{Δ r_{n}} = \vec{d v_{n}} Δ t,

23

\vec{Δ r_{t}} = \vec{d v_{t}} Δ t .

The calculation method of force in PFC linear model is:

24

\vec{Δ F_{n}} = k_{n} \vec{Δ r_{n}},

25

\vec{Δ F_{t}} = k_{t} \vec{Δ r_{t}} .

The equation of motion of particles according to Newton’s second law is as follows:

26

\sum \vec{F} = m \frac{\vec{d v}}{d t} = m \frac{{\vec{d r}}^{2}}{d^{2} t},

27

\sum \vec{M} = I \frac{\vec{d w}}{d t} = I \frac{{\vec{d θ}}^{2}}{d^{2} t},

where $I$ is the inertia moment of the particle, in the linear contact model, it is generally considered that the moment at the contact point is zero, where $\sum \vec{F}$ is subjected to the combined force of contact force and gravity.

The mesoscopic parameters are updated in each step of simulation. For example, particle a, the force is calculated as:

28

\vec{F_{n} (t + Δ t)} = \vec{F_{n} (t)} + \vec{Δ F_{n} (t)},

29

\vec{F_{t} (t + Δ t)} = \vec{F_{t} (t)} + \vec{Δ F_{t} (t)} .

The velocity is updated as:

30

\vec{v_{a} (t + Δ t)} = \vec{v_{a} (t)} + \frac{\sum \vec{F}}{m} Δ t,

31

\vec{w_{a} (t + Δ t)} = \vec{w_{a} (t)} + \frac{\sum \vec{M}}{I} Δ t .

The particle position and rotation angle is updated as:

32

\vec{r_{a} (t + Δ t)} = \vec{r_{a} (t)} + \vec{v_{a} (t + \frac{Δ t}{2})} Δ t,

33

\vec{θ_{a} (t + Δ t)} = \vec{θ_{a} (t)} + \vec{v_{a} (t + \frac{Δ t}{2})} Δ t .

3.4. Discrete element model

The silo model with a radius of 250 mm and a height of 1000 mm is established according to the geometry of experimental silo. The wall element would be used to simulate the silo wall. The multi-element particles with 6 mm major axis diameter and 4 mm minor axis diameter would be used to simulate non-spherical particles. The dust particles are simulated by ball elements with 0.5 mm diameter, the dust particles added in model with a ratio of 10:1. (The traditional model would only use the spherical particles with diameter of 5 mm). The volume of ball element used in the traditional ball model is 19.63, and that of multi-element particle in the improved model is 18.84, which is 4.02 % lower than the traditional model. The ten sections of walls would be built on both sides according to the arrangement of monitoring points in the experiment. The normal pressure of each wall section is established to monitor and record the dynamic pressure, which makes the same effect as the monitoring points in the experiment.

The parameters are selected with the laboratory measurement and the mechanical properties of grain [29-31]. Through the parameter calibration method [32-34], the physical and mechanical parameters is adjusted to achieve that, the static storage normal pressure in simulation is in accordance with that measured in experiment. The parameters determined are listed in Table 1. In Table 1, the wall, ball and clump elements represent the wall, spherical particles and non-spherical grain particles, respectively, the parameters selected for the mechanical contact model of wall and particle are listed in Table 2, and $k_{n}$ , $k_{s}$ are defined as their normal and tangential stiffness.

Table 1The main physical parameters in the simulation

	Parameter category	Numerical value
Spherical ball model	Ball density / (kg·m^-3)	1000
	Ball friction coefficient	0.43
	Wall friction coefficient	0.62
	Particle damp coefficient	0.05
Improved multi-element model	Ball density / (kg·m^-3)	2000
	Clump density / (kg·m^-3)	1000
	Ball friction coefficient	0.3
	Clump friction coefficient	0.3
	Wall friction coefficient	0.62
	Particle damp coefficient	0.05

Table 2Mechanics parameters of particle and wall in simulation

	Category	Numerical value
Spherical ball model	Wall-kn / (N·m^-1)	3.2e6
	Wall-ks / (N·m^-1)	1.6e6
	Ball-kn / (N·m^-1)	3.2e5
	Ball-ks / (N·m^-1)	1.6e5
Improved multi-element model	Wall-kn / (N·m^-1)	3.2e6
	Wall-ks / (N·m^-1)	1.6e6
	Clump-kn / (N·m^-1)	3.2e5
	Clump-ks / (N·m^-1)	1.6e5
	Ball-kn / (N·m^-1)	3.2e6
	Ball-ks / (N·m^-1)	1.6e6

4. Results and discussion

4.1. Fill simulation

The traditional spherical particles or the improved multi-element particles would fill into the silo by the method of central fill with properties selected according to the calculation ability of computer and the parameter calibration method mentioned above. The particles would operate just as the linear contact model, which calculate as the contact model and the update method in Chapter 2.

Because the filling process would be a long computing time and the calculation would be complicated if the particles internal friction coefficient is large, so a new filling method is adopted, which the particles internal friction coefficient is set to zero during filling. The particles internal friction coefficient is listed in Table 1 and Table 2 by “the ball property (clump property)” command after the filling process is completed, then iterate for a certain period of time to achieve stability (Fig. 9).

The traditional spherical particles model contains 23,000 ball elements and the storage height is 0.994 m. The improved multi-element particles model contains 24676 clump elements and 2382 small ball elements with a storage height of 1.013. The scale of the two models is similar.

Fig. 9Static storage condition: a) traditional spherical particles model, b) improved multi-element model

a)

b)

4.2. Simulation & experiment

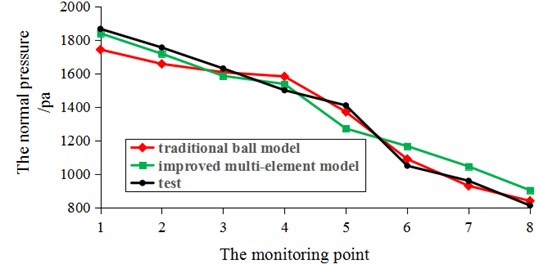
Because this research focus on the grain discharge process of the cylindrical silos, it is unnecessary to determine the flow pattern is the mass flow or the funnel flow. Therefore, this paper uses the pressure to verify whether the simulation is consistent with the experiment. Comparing the normal pressure of silo wall in storage condition with the pressure obtained by the experiment in the Chapter 2, the results demonstrate that the results from simulation, experiment and the trend of pressure match well, which can verify the authenticity of the simulation model. The comparison of dynamic pressure in the following further validated the proposed simulation model.

Fig. 10Static storage wall pressure value

4.3. Comparison

4.3.1. Normal wall pressure

Since the pressure at the monitoring points of the silo upper part is small and after a period of discharge the pressure of the upper part monitoring points would be zero, which would introduce observation difficult, only three monitoring points (1.3.5) were selected to analyze the dynamic normal pressure in grain discharge (Fig. 11).

Fig. 11Dynamic pressure simulation results: a) the traditional spherical ball model, b) the improved multi-element particle model

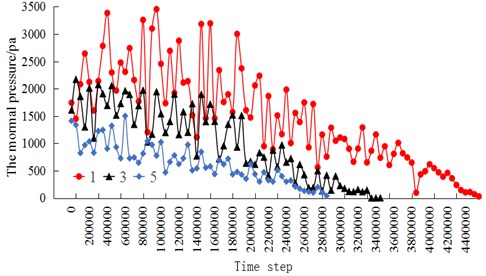
a)

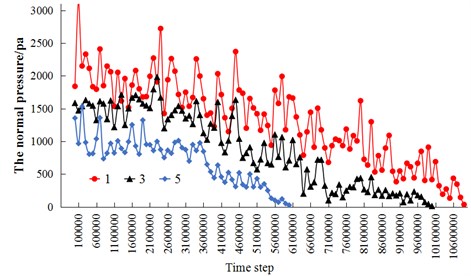
b)

It is demonstrated that, the dynamic pressure decreases with the decreases of depth in two models, which is consistent with the results provided in [35-37]. The traditional spherical ball model iterated 4500000 steps to discharge, the real time of discharge is 29.1 s, while the improved multi-element model iterates 10800000 steps to discharge, and the real time is 31.4 s. It indicates that the discharge time of improved multi-element model is longer and the outflow is more stagnant.

Taking the No. 1 monitoring point for analysis, the dynamic normal pressure during discharge calculated by the traditional spherical ball model and the improved multi-element model is compared with the experimental results (Fig. 12).

Fig. 12Comparison of dynamic pressure during discharge process

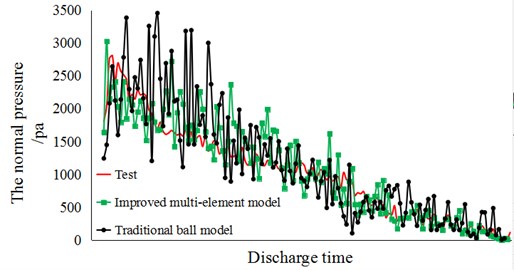
It is demonstrated that, the pressure of simulation models fluctuates more volatile, but the dynamic pressure trend is similar; the simulation values fluctuate around the experimental values. The other monitoring points illustrate similar laws, which can further verify the authenticity of the simulation model. The pressure fluctuation amplitude of the improved multi-element model is smaller, and the fluctuation trend is gentler, which is related to the inter-locking between particles, and the inter-friction coefficient of the improved multi-element model is more sufficient than that of the traditional ball model in flow.

The error of simulation could be calculated as:

34

W = \frac{\sum_{1}^{n} \sqrt{(p_{A} - p_{B})^{2} / {p_{B}}^{2}}}{n},

where $p_{A}$ is defined as the simulation pressure of improved multi-element model or the traditional spherical ball model, $p_{B}$ is the experimental results. It is calculated that the deviation of the improved multi-element model is 11.28 %, while that of the traditional model is 29.175 %, it demonstrates that the improved multi-element model effectively improve the accuracy of dynamic pressure during discharge.

Table 3Dynamic maximum pressure value comparison

Monitor points	Test	Spherical ball model	Deviation	Improved model	Deviation
1	2845.540	3455.140	21.44 %	3027.398	6.39 %
3	1906.340	2170.029	13.85 %	1982.010	3.98 %
5	1679.017	1501.752	10.63 %	1531.333	8.81 %
7	1056.897	1232.434	16.74 %	1123.435	6.34 %

4.3.2. Porosity and coordination number

For the improved multi-element model, the “measure circle” command provided by PFC is used to establish the measure circle in the silo (Fig. 13). Comparing the meso-structural parameters of the improved multi-element model and the traditional ball model, the meso-mechanical behaviors of the two models would be analyzed as follows.

Fig. 13The position of measure circles

The method for determining porosity as Eq. (35) could be inferred from the definition of porosity [38]. Where $V$ is the grain accumulation volume, $V_{p}$ is the sum volume of stored grain particles:

35

n = \frac{V - V_{p}}{V} .

The porosity of the laboratory test results is 40.04 % in the static storage state. The average porosity of nine measure circles in the 2D model, which is transformed from the porosity [39]:

36

ε_{3 d} = 1 - ξ (1 - ε_{2 d}),

37

ξ = \frac{2}{\sqrt{π \sqrt{3}}} + D_{r} (\frac{2}{\sqrt{π \sqrt{3}}} - \frac{\sqrt{2}}{\sqrt{π \sqrt{3}}}),

where $D_{r}$ is the relative compaction of grain, $D_{r} = \frac{e_{m a x} - e}{e_{m a x} - e_{m i n}}$ , $e_{m a x}$ , $e_{m i n}$ , $e$ are the maximum, the minimum and the test void ratios in laboratory tests, respectively. $ε_{2 d}$ is two-dimensional porosity of grain, $ε_{3 d}$ is three-dimensional porosity of grain.

It is calculated that the porosity of the improved multi-element model is 39.13 % and the error is 2.27 % in the three-dimensional state, while the porosity of the spherical ball model is 42.20 % and the difference is 5.39 %. The packing porosity decreased by 3.07 % and the accuracy of the improved model is increased by 3.12 % in simulation.

The coordination number is also one of the important meso-structural parameters, which would be used to characterize the compactness of the accumulated particles like porosity. The coordination number is defined as the number of particles in contact with a certain particle, and the coordination number is inversely proportional to the porosity [40]. The coordination number of the traditional ball model is 3.67 and that of the improved multi-element model is 4.66, which indicates that the improved multi-element model could effectively increase the coordination number of the particle assemble. In terms of meso-structural parameters, the improved multi-element model makes the grain denser and more in accord with the actual situation of grain storage [41].

4.3.3. Dynamic force chain

The dynamic changes of the meso-mechanics were analyzed by comparing the force chain diagrams of the two models at the mechanical time of 2.4 s (Fig. 14).

Fig. 14The diagram of dynamic force chains: a) traditional spherical ball model, b) improved multi-element particle model

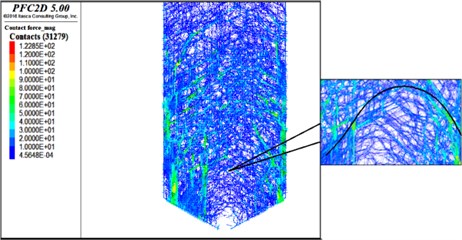
a)

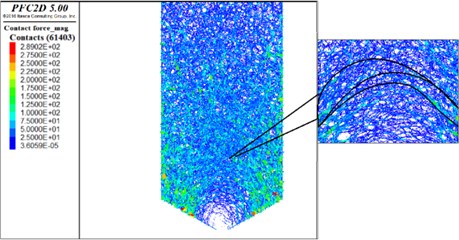
b)

The substantial particle chains are easily formed between multi-element particles to resist external forces because of the inter-locking between particles [42-44].

It could be clearly found that the number of contact forces of the traditional spherical ball model is 31279, and that of the improved multi-element model is 61403. It indicates that the force chain of the improved multi-element model is denser, and the force network is more complex. As shown in the local force chain diagram of the two models (Fig. 15), the contact force distribution of the improved multi-element model is more uniform. There are several transverse arching force chains observed clearly in the improved multi-element model. The arch occurs frequently during discharge [45]. The simulation results of multi-element model could more clearly reflect the law of instantaneous arch which.

5. Conclusions

The PFC simulation was developed to simulate the non-spherical particles discharge with multi-element model considering the effect of dust content with ball elements. The numerical simulation was carried out by using the improved multi-element model on the basis of the experiment, and the simulation results of improved multi-element model were compared with those of the traditional spherical ball model. The research indicated that, the particle shape not only affects the macro-mechanical behavior during flow, but also affects the meso-structure of particles and the dynamic force chains evolution in flow. The specific conclusions are as follows:

1) In terms of macroscopic wall pressure, the dynamic pressure fluctuation during discharge simulated with improved multi-element particle model is more gradual, and the discharge process lasts longer. The error, which by comparing the results of dynamic pressure obtained from simulation and experiment, of the improved multi-element particle model is 11.28 %, while the error of the traditional spherical model is 29.175 %. The error of the improved multi-element model is 17.895 % lower than that of the traditional spherical ball model. The normal pressure simulation results are more accurate than the traditional ball model.

2) In terms of the meso-structure of the granular material, the packing porosity of the traditional spherical particle model is 42.20 %, the coordination number is 3.67, while the material packing porosity of the improved model is 39.13 %, the coordination number is 4.66. And the packing porosity decrease by 3.07 %, the accuracy of the improved model increased by 3.12 %, and the coordination number increase by 0.99. The improved multi-element model can effectively increase the density of particle accumulation, and more in consistent with the actual situation.

3) The particle shape affects the meso-mechanical behavior of particles. The simulation demonstrates that, compared with the traditional spherical ball model, the number of contact forces in the improved multi-element model increases by 30124, the distribution of contact force chains is more uniform and dense, and several arching force chains could be clearly observed in the improved multi-element model, which more clearly reflect the law of the instantaneous arch.

This research proved that the particle shape has a significant effect on the macroscopic and mesoscopic porosities of granular materials. The improved multi-element particles established in this paper would further improve the accuracy of simulation; the comprehension of the ﬂow behaviors for non-spherical granular materials in the silo is important to the design and application of silos. The research has an important reference value for further simulation of non-spherical grain particles’ flow mechanism in the silo. In the field of engineering application, the improved model could be used to simulate and predict the wall pressure of silos and provide guidance for silo design.

References

Boac J. M., Ambrose R. P. K., Casada M. E., et al. Applications of discrete element method in modeling of grain postharvest operations. Food Engineering Reviews, Vol. 6, Issue 4, 2014, p. 128-149.

Publisher
Choi J., Kudrolli A., Bazant M. Z. Velocity profile of granular flows inside silos and hoppers. Journal of Physics: Condensed Matter, Vol. 17, Issue 24, 2005, p. S2533.

Publisher
González Montellano C., Ramírez Á., Gallego E., et al. Validation and experimental calibration of 3D discrete element models for the simulation of the discharge flow in silos. Chemical Engineering Science, Vol. 66, Issue 21, 2011, p. 5116-5126.

Publisher
Umer M., Siraj M. S. DEM studies of polydisperse wet granular flows. Powder Technology, Vol. 328, 2018, p. 309-317.

Publisher
Tian T., Su J., Zhan J., et al. Discrete and continuum modeling of granular flow in silo discharge. Particuology, Vol. 36, 2018, p. 127-138.

Publisher
Nasato D. S., Goniva C., Pirker S., et al. Coarse graining for large-scale DEM simulations of particle flow – an investigation on contact and cohesion models. Procedia Engineering, Vol. 102, 2015, p. 1484-1490.

Publisher
Kobyłka R., Horabik J., Molenda M. Numerical simulation of the dynamic response due to discharge initiation of the grain silo. International Journal of Solids and Structures, Vol. 106, Issue 107, 2017, p. 27-37.

Publisher
Ramírez A., Nielsen J., Ayuga F. On the use of plate-type normal pressure cells in silos. Computers and Electronics in Agriculture, Vol. 71, Issue 1, 2010, p. 64-70.

Publisher
Wang P., Zhu L., Zhu X. Flow pattern and normal pressure distribution in flat bottom silo discharged using wall outlet. Powder Technology, Vol. 295, 2016, p. 104-114.

Publisher
González Montellano C., Ayuga F., Ooi J. Y. Discrete element modelling of grain flow in a planar silo: Influence of simulation parameters. Granular Matter, Vol. 13, Issue 2, 2010, p. 149-158.

Publisher
Tao H., Jin B., Zhong W., et al. Discrete element method modeling of non-spherical granular flow in rectangular hopper. Chemical Engineering and Processing: Process Intensification, Vol. 49, Issue 2, 2010, p. 151-158.

Publisher
Horabik J., Parafiniuk P., Molenda M. Stress profile in bulk of seeds in a shallow model silo as influenced by mobilisation of particle-particle and particle-wall friction: experiments and DEM simulations. Powder Technology, Vol. 327, 2018, p. 320-334.

Publisher
Li J., Langston P. A., Webb C., et al. Flow of sphero-disc particles in rectangular hoppers – a DEM and experimental comparison in 3D. Chemical Engineering Science, Vol. 59, Issue 24, 2004, p. 5917-5929.

Publisher
Grof Z., Kohout M., Štěpánek F. Multi-scale simulation of needle-shaped particle breakage under uniaxial compaction. Chemical Engineering Science, Vol. 62, Issue 5, 2007, p. 1418-1429.

Publisher
Liu S. D., Zhou Z. Y., Zou R. P., et al. Flow characteristics and discharge rate of ellipsoidal particles in a flat bottom hopper. Powder Technology, Vol. 253, 2014, p. 70-79.

Publisher
Yu Y., Saxén H. Discrete element method simulation of properties of a 3 conical hopper with mono-sized spheres. Advanced Powder Technology, Vol. 22, Issue 3, 2011, p. 324-331.

Publisher
Wan J., Wang F., Yang G., et al. The influence of orifice shape on the flow rate: A DEM and experimental research in 3D hopper granular flows. Powder Technology, Vol. 335, 2018, p. 147-155.

Publisher
Zhang Y. X., Jia F. G., Zeng Y., et al. DEM study in the critical height of flow mechanism transition in a conical silo. Powder Technology, Vol. 331, 2018, p. 98-106.

Publisher
You Y., Zhao Y. Discrete element modelling of ellipsoidal particles using super-ellipsoids and multi-spheres: a comparative study. Powder Technology, Vol. 331, 2018, p. 179-191.

Publisher
Lu G., Third J. R., Müller C. R. Discrete element models for non-spherical particle systems: from theoretical developments to applications. Chemical Engineering Science, Vol. 127, 2015, p. 425-465.

Publisher
Soltanbeigi B., Podlozhnyuk A., Papanicolopulos S.-A., et al. DEM study of mechanical characteristics of multi-spherical and superquadric particles at micro and macro scales. Powder Technology, Vol. 329, 2018, p. 288-303.

Publisher
Coetzee C. J. Calibration of the discrete element method and the effect of particle shape. Powder Technology, Vol. 297, 2016, p. 50-70.

Publisher
Li Y., Gui N., Yang X., et al. Numerical study of gravity-driven dense granular flows on flow behavior characterization. Powder Technology, Vol. 297, 2016, p. 144-152.

Publisher
Höhner D., Wirtz S., Scherer V. A numerical study on the influence of particle shape on hopper discharge within the polyhedral and multi-sphere discrete element method. Powder Technology, Vol. 226, 2012, p. 16-28.

Publisher
Lu G., Third J. R., Müller C. R. Critical assessment of two approaches for evaluating contacts between super-quadric shaped particles in DEM simulations. Chemical Engineering Science, Vol. 78, 2012, p. 226-235.

Publisher
Balevičius R., Kačianauskas R., Mróz Z., et al. Analysis and DEM simulation of granular material flow patterns in hopper models of different shapes. Advanced Powder Technology, Vol. 22, Issue 2, 2011, p. 226-235.

Publisher
Ai J., Chen J.-F., Rotter J. M., et al. Assessment of rolling resistance models in discrete element simulations. Powder Technology, Vol. 206, Issue 3, 2011, p. 269-282.

Publisher
Cleary P. W., Sawley M. L. DEM modelling of industrial granular flows: 3D case studies and the effect of particle shape on hopper discharge. Applied Mathematical Modelling, Vol. 26, 2002, p. 89-111.

Publisher
Patwa A., Ambrose R. P. K., Casada M. E. Discrete element method as an approach to model the wheat milling process. Powder Technology, Vol. 302, 2016, p. 350-356.

Publisher
González Montellano C., Fuentes J. M., Ayuga Téllez E., et al. Determination of the mechanical properties of maize grains and olives required for use in DEM simulations. Journal of Food Engineering, Vol. 111, Issue 4, 2012, p. 553-562.

Publisher
Grima A. P., Wypych P. W. Investigation into calibration of discrete element model parameters for scale-up and validation of particle-structure interactions under impact conditions. Powder Technology, Vol. 212, Issue 1, 2011, p. 198-209.

Publisher
Albaraki S., Antony S. J. How does internal angle of hoppers affect granular flow? Experimental studies using digital particle image velocimetry. Powder Technology, Vol. 268, 2014, p. 253-260.

Publisher
Mak J., Chen Y., Sadek M. A. Determining parameters of a discrete element model for soil-tool interaction. Soil and Tillage Research, Vol. 118, 2012, p. 117-122.

Publisher
Albaba A., Lambert S., Nicot F., et al. Relation between microstructure and loading applied by a granular flow to a rigid wall using DEM modeling. Granular Matter, Vol. 17, Issue 5, 2015, p. 603-616.

Publisher
Couto A., Ruiz A., Aguado P. J. Experimental study of the pressures exerted by wheat stored in slender cylindrical silos, varying the flow rate of material during discharge. Comparison with Eurocode 1 part 4. Powder Technology, Vol. 237, 2013, p. 450-467.

Publisher
Wang Y., Lu Y., Ooi J. Y. Finite element modelling of wall pressures in a cylindrical silo with conical hopper using an arbitrary Lagrangian-Eulerian formulation. Powder Technology, Vol. 257, 2014, p. 181-190.

Publisher
Wójcik M., Sondej M., Rejowski K., et al. Full-scale experiments on wheat flow in steel silo composed of corrugated walls and columns. Powder Technology, Vol. 311, 2017, p. 537-555.

Publisher
Gan J. Q., Yu A. B., Zhou Z. Y. DEM simulation on the packing of fine ellipsoids. Chemical Engineering Science, Vol. 156, 2016, p. 64-76.

Publisher
Wang Z., Ruiken A., Jacobs F., et al. A new suggestion for determining 2D porosities in DEM studies. Geomechanics and Engineering, Vol. 7, 2014, p. 665-678.

Publisher
Jiang X., Liu E., Jiang L., et al. Evolution of meso-structures and mechanical properties of granular materials under triaxial compression state from complex network perspective. Granular Matter, Vol. 20, 3, p. 2018-54.

Publisher
Kasraei M., Nejadi J., Shafiei S. Relationships between grain physicochemical and mechanical properties of some Iranian wheat cultivars. Journal of Agriculture Science Technology, Vol. 17, 2015, p. 635-647.

Search CrossRef
He Y., Evans T. J., Shen Y. S., et al. Discrete modelling of the compaction of non-spherical particles using a multi-sphere approach. Minerals Engineering, Vol. 117, 2018, p. 108-116.

Publisher
Khazeni A., Mansourpour Z. Influence of non-spherical shape approximation on DEM simulation accuracy by multi-sphere method. Powder Technology, Vol. 332, 2018, p. 265-278.

Publisher
Villagrán Olivares M. C., Benito J. G., Uñac R. O., et al. Towards a one parameter equation for a silo discharging model with inclined outlets. Powder Technology, Vol. 336, 2018, p. 265-272.

Publisher
Rubio Largo S.-M., Janda A., Maza D., et al. Disentangling the free-fall arch paradox in silo discharge. Physical Review Letters, Vol. 114, Issue 23, 2015, p. 238002.

Publisher

About this article

Received

29 January 2019

Accepted

12 March 2019

Published

30 June 2019

DOI

https://doi.org/10.21595/jve.2019.20558

Keywords

improved multi-element model

PFC numerical simulation

particle shape

macro and meso mechanical mechanism

Acknowledgements

Our deepest gratitude goes first and foremost to the National Science Foundation Project of China 51708182 for their fund support.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2021 06 28

Numerical simulation of pneumatic conveying characteristics of micron particles in horizontal pipe

Si Qin, Xiaojun Zhou

Research article

2019 06 30

Numerical simulation of hydraulic fracturing in transversely isotropic rock masses based on PFC-2D

Lei Xia, Yawu Zeng

Research article

2019 06 30

Dynamic simulation analysis of elastic overpressure fluctuation on silo wall for the arch action

Yong Feng, Jie Liu

Research article

2019 06 30

Relationship of rock microscopic parameters with the elastic modulus and strength

Yanhui Cheng, Weijun Yang, Dongliang He

Y. Feng and Z. Yuan, “Macroscopic and microscopic simulation of silo granular flow based on improved multi-element model,” Journal of Vibroengineering, Vol. 21, No. 4, pp. 848–863, Jun. 2019, https://doi.org/10.21595/jve.2019.20558

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2019.20558
UR  - https://doi.org/10.21595/jve.2019.20558
TI  - Macroscopic and microscopic simulation of silo granular flow based on improved multi-element model
T2  - Journal of Vibroengineering
AU  - Yuan, Ziran
AU  - Feng, Yong
PY  - 2019
DA  - 2019/06/30
PB  - JVE International Ltd.
SP  - 848-863
IS  - 4
VL  - 21
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Yuan_2019,
	doi = {10.21595/jve.2019.20558},
	url = {https://doi.org/10.21595/jve.2019.20558},
	year = 2019,
	month = {jun},
	publisher = {{JVE} International Ltd.},
	volume = {21},
	number = {4},
	pages = {848--863},
	author = {Ziran Yuan and Yong Feng},
	title = {Macroscopic and microscopic simulation of silo granular flow based on improved multi-element model},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]Z. Yuan and Y. Feng, “Macroscopic and microscopic simulation of silo granular flow based on improved multi-element model,” Journal of Vibroengineering, vol. 21, no. 4, pp. 848–863, Jun. 2019, doi: 10.21595/jve.2019.20558.

Copy IEEE

Copied to clipboard!

Yuan, Ziran, and Yong Feng. “Macroscopic and Microscopic Simulation of Silo Granular Flow Based on Improved Multi-Element Model.” Journal of Vibroengineering 21, no. 4 (June 30, 2019): 848–63. https://doi.org/10.21595/jve.2019.20558.

Copy Chicago

Copied to clipboard!

Macroscopic and microscopic simulation of silo granular flow based on improved multi-element model

Abstract

Highlights

1. Introduction

2. Experiment test

3. Numerical models

3.1. Improved multi-element model

3.2. Contact model

3.2.1. Contact between particles

3.2.2. Contact between particle and wall

3.3. Equations of particle motion

3.4. Discrete element model

4. Results and discussion

4.1. Fill simulation

4.2. Simulation & experiment

4.3. Comparison

4.3.1. Normal wall pressure

4.3.2. Porosity and coordination number

4.3.3. Dynamic force chain

5. Conclusions

References

About this article

Related Articles