Abstract
A series of dynamic triaxial tests were performed to investigate the dynamic deformation properties of the muck soil, in the Pearl River Delta region of Shenzhen, China, under different consolidation ratios, loading frequencies and cyclic stress with SPAX-2000 triaxial testing system. The results showed that the initial stress-strain hysteresis curve of the muck soil under the low-frequency cyclic loading developed rapidly and the curve shape changes from sparse to tight and to slightly sparse. The cumulative plastic strain of muck soil increased nonlinearly with the dynamic stress amplitude, and there was a critical dynamic stress. As the dynamic stress amplitude reached its critical value, the strain increased sharply and the soil microstructure was destroyed. There was a frequency threshold between 0.25 Hz and 0.5 Hz, and the cumulative plastic strain development mode was from stable model to over-destructive model. The stiffness of the muck decreased gradually, and the plastic deformation increased as the number of cycles increased. Therefore, the lower the loading frequency developed, the greater the plastic deformation would be. The dynamic elastic modulus decreased as the plastic deformation increased, while the dynamic elastic modulus increased as the consolidation stress increased. Moreover, the empirical formulas of dynamic elastic modulus and plastic strain index were established with the consolidation stress ratio as the parameter, and the validity was verified by experimental data.
Highlights
- The marine soft soil taken from the Pearl River Delta region of Shenzhen in China, was higher than that of other tests in water content.
- To investigate the dynamic deformation properties of the muck soil under different loading frequencies and cyclic stress, a series of dynamic triaxial tests were performed by SPAX–2000 system.
- Several curves were obtained, including typical hysteresis curves under different frequency loading, curves of the cumulative plastic strain and the number of cycles under different stress amplitude.
- According to the test data, the dynamic elastic modulus-exponential function relationship model was established.
1. Introduction
Muck is widely distributed in coastal areas and inland lakes [1, 2]. With the large-scale construction of houses, roads, railways and urban traffic engineering in soft soil areas, and the rapid development of offshore platforms, many new geotechnical problems arise. The dynamic characteristics of soft soil and its composite foundation under cyclic loading (seismic loading, traffic loading, wave loading) have attracted wide attention [3-5]. As early as the 1960s, Hardin [6-8], Yashuara [9], Chai [10] et. al used the improved dynamic triaxial instrument to study the dynamic modulus, dynamic damping ratio and dynamic cumulative plastic deformation of soil properties. Boulanger [11] conducted a staged loading triaxial test with Sherman soft soil in California, and analyzed the effects of loading frequency, stress history, cycle number, and soil structure on dynamic parameters. The relationship between normalized shear modulus, damping ratio and shear strain, consolidation stress and loading frequency of soft soil was built [12]. References [13, 14] presented a relationship between the dynamic stress and dynamic strain of soft clay under traffic loading, there existed a critical dynamic stress ratio and vibration frequency threshold value at the dynamic stress-dynamic strain curve.
Many valuable test results about dynamic properties of soft soil have been achieved in previous studies [15-23], however, the following problems still exist: (1) Most of the soil samples used in the past research were soft clay with non-high water content, non-strong structure and low-permeability; (2) The loading frequency was mostly greater than 1 Hz, while low-frequency (less than 1 Hz) traffic load research had rarely been reported in previous references; (3) Most of the analysis models of deformation, such as cumulative plastic strain model and softening model did not consider the influence of consolidation stress (the intermediate principal stress); (4) Soft soils have different composition, structural structure and physical properties due to their different formation environments which produces great variation on the properties of dynamic deformation [24, 25].
This paper mainly addressed the second issue. A series of dynamic triaxial tests were performed to investigate the dynamic deformation properties of the muck soil, in the Pearl River Delta region of Shenzhen, China, under the conditions of different consolidation ratios, loading frequencies and cyclic stress with SPAX-2000 real triaxial test system. Based on the data, the empirical formula of dynamic elastic modulus was established. It can provide a theoretical basis for the establishment of the soil constitutive model and the structural dynamic response analysis.
2. Dynamic triaxial test of muck
2.1. Tested soils
The studied soils were taken from a construction site in Shenzhen which was located in the offshore area of the alluvial plain of the Pearl River estuary. The sampling depth was 14 meters below sea level. The undisturbed muck soils were obtained by the professional thin-walled earth borrowers. The physical and mechanical properties are as follows: the natural density is 1.63 g/cm3, the water content is 65.2 % (The partial samples water content exceed 70 %), the relative density of soil particles is 2.69, the void ratio is 1.72, the plasticity index is 20.9, the liquidity index is 1.06, compression coefficient is 1.43 MPa-1, the cohesion is 7.0 kPa, internal friction angle is 2.1°.
2.2. Experimental instrument and scheme
2.2.1. Experimental instrument
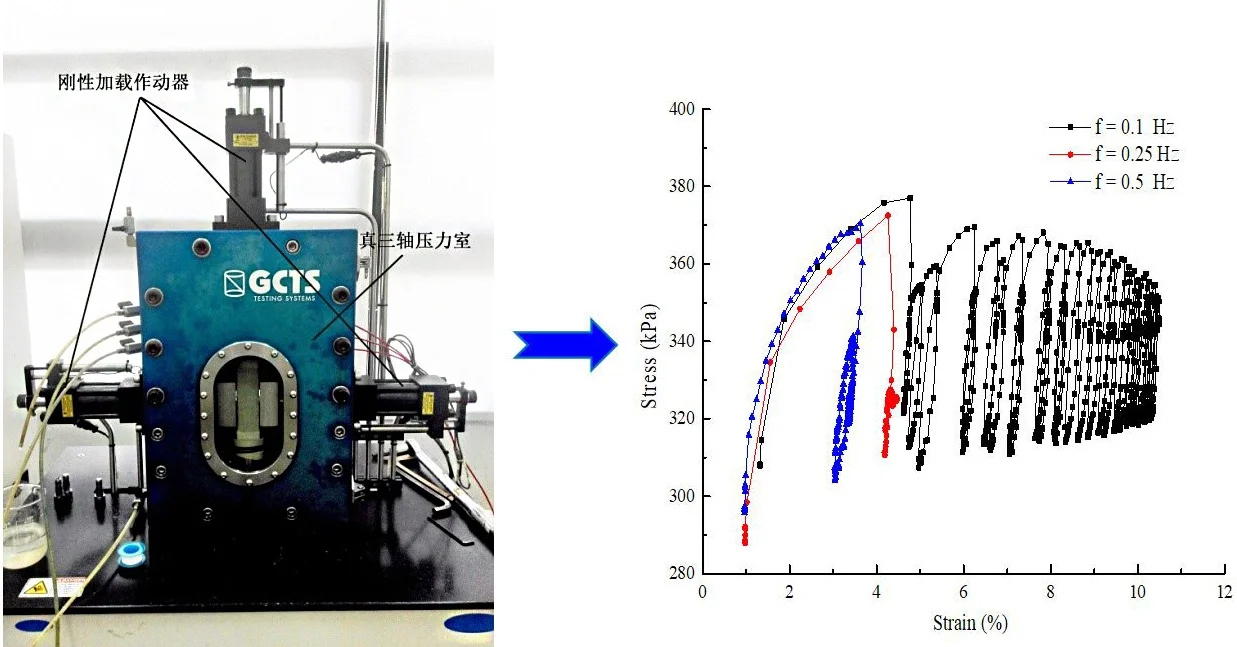
The dynamic triaxial experiment was performed with the SPAX-2000 testing system produced by GCTS of USA, shown in Fig. 1. The system consists of seven parts, including pressure control panel, pressure chamber, confining pressure/volume computer servo controller, back pressure/pore pressure volume computer servo controller, digital servo controller and acquisition system, variant constant pressure oil pump, control and software.
Fig. 1SPAX-2000 true triaxial testing system

2.2.2. Experimental scheme
This test focused on three factors on the dynamic deformation characteristics of muck: loading frequency, cyclic stress amplitude and consolidation stress. Table 1 The schemes of the test:
(1) Confining pressure and consolidation ratio: according to the sampling depth of the soil sample, the confining pressure was 200 kPa; the consolidation ratios were 1.0, 1.2 and 1.5.
(2) Loading frequency: according to the results of on-site inspection by Zhang et al. [8], the loading frequency of the subway was mostly in the range of 0.4 Hz to 2.6 Hz, the road loading frequency was mainly from 0.2 Hz to 0.5 Hz. There were a lot of research results on cycle frequency greater than 1 Hz. Thus, the load vibration frequencies were selected to be 0.1 Hz, 0.25 Hz, 0.5 Hz, and 1 Hz.
(3) Cyclic stress amplitude: considering the dynamic loading simulation conditions, soil compressive high compressibility, high water content soft clay (up to 70 %) and critical dynamic consolidation stress ratio, etc., the cyclic stress amplitude were 20 kPa, 50 kPa and 65 kPa.
Table 1The schemes of the test
Sample number | Second principal stress ( / kPa) | Consolidation ratios | Frequency (ƒ / Hz) | Stress amplitude ( / kPa) |
N1 | 200 | 1.0 | 0.1 | 20 |
N2 | 200 | 1.2 | 0.5 | 20 |
N3 | 200 | 1.5 | 1 | 20 |
N4 | 200 | 1.0 | 0.1 | 50 |
N5 | 200 | 1.2 | 0.5 | 50 |
N6 | 200 | 1.5 | 1 | 50 |
N7 | 200 | 1.0 | 0.1 | 65 |
N8 | 200 | 1.2 | 0.5 | 65 |
N9 | 200 | 1.5 | 1 | 65 |
N10 | 225 | 1.0 | 0.1 | 20 |
N11 | 225 | 1.2 | 0.5 | 20 |
N12 | 225 | 1.5 | 1 | 20 |
N13 | 225 | 1.0 | 0.1 | 50 |
N14 | 225 | 1.2 | 0.5 | 50 |
N15 | 225 | 1.5 | 1 | 50 |
N16 | 225 | 1.0 | 0.1 | 65 |
N17 | 225 | 1.2 | 0.5 | 65 |
N18 | 225 | 1.5 | 1 | 65 |
N19 | 250 | 1.0 | 0.1 | 20 |
N20 | 250 | 1.2 | 0.5 | 20 |
N21 | 250 | 1.5 | 1 | 20 |
N22 | 250 | 1.0 | 0.1 | 50 |
N23 | 250 | 1.2 | 0.5 | 50 |
N24 | 250 | 1.5 | 1 | 50 |
N25 | 250 | 1.0 | 0.1 | 65 |
N26 | 250 | 1.2 | 0.5 | 65 |
N27 | 250 | 1.5 | 1 | 65 |
N28 | 200 | 1.0 | 0.25 | 20 |
N29 | 200 | 1.2 | 0.25 | 50 |
N30 | 250 | 1.5 | 0.25 | 50 |
2.2.3. Experimental procedure
These tests comprised the following steps:
Step 1: The undisturbed muck soils were prepared for some rectangular parallelepiped specimens of 50 mm×50 mm×120 mm, put into vacuum saturation for 48 hours, and charged into a pressure chamber for back pressure saturation to ensure saturation of not less than 95 %.
Step 2: The soil specimen was consolidated under a certain consolidation pressure.
Step 3: When the drain valve closed, the static biasing stress was applied to the specimen by controlling the upper pressure plate. The sinusoidal wave loading was applied to perform the undrained shear test, and the axial deformation of the sample was up to 15 %. The maximum number of loadings was 5000 times.
If the specimens were not broken after the set number of cycles, the shear stress would be on the specimen with the shear rate of 0.01 %/min until it was broken. Then the test was finished.
3. Results and interpretation
3.1. Influence of loading frequency on dynamic deformation
(1) Characteristics of stress-strain hysteresis curves.
The stress-strain hysteresis curves contain a lot of information which could reflect kinetic parameters such as energy loss, dynamic elastic modulus, and damping ratio. The typical stress-strain hysteresis curves are shown in Fig. 2. Each stress-strain hysteresis loop is divided into two phases-loading and unloading. The length of the -axis represents the plastic strain generates during the loading and unloading phase.
Fig. 2Typical hysteresis curves under different frequency loading: (Dynamic stress amplitude σd= 65 kPa, effective stress σ1'=σ2'= 250 kPa, σ3'= 200 kPa)
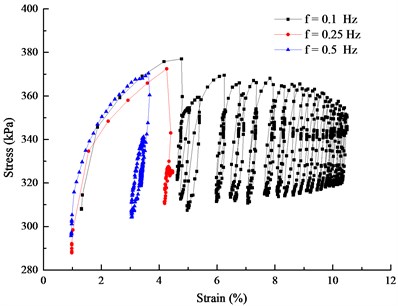
As shown in Fig. 2, the development patterns of muck soil hysteresis curves are similar under the same consolidation pressure, cyclic stress amplitude and different loading frequency cyclic loading. The initial stress-strain hysteresis curve of the muck under the low-frequency cyclic loading developed rapidly. Its curve shape change from sparse to tight and then change to slightly sparse. The higher the frequency developed, the earlier the tight phase would be and the hysteresis loop would be closer. Results show that the shorter the time of the load under the high frequency loading, and the plastic strain development and the loss of energy were limited. Therefore, the area of a single hysteresis loop with a high frequency was relatively small and the degree of closure was higher than the low frequency condition. The energy of the loss increased as the stress amplitude increased, so that the area of the hysteresis loop and the length of the open section increased with the increasing of the stress amplitude under the same cycle frequency and number of times. When the consolidation stress was large, the arrangement of the particles was tight. The hysteresis loop entered the compact phase early, which means the soil entered the elastic phase earlier.
(2) Characteristics of cumulative plastic strain.
Fig. 3(a) and (b) present the relationship between cumulative plastic strain and number of cycles under the isotropic consolidation, different frequency and the same cyclic stress amplitude ( 20 kPa and 50 kPa). The typical curves of - under the anisobaric consolidation are shown in Fig. 3(c).
As shown in Fig. 3, the following three characteristics are found from - curves.
Fig. 3Curves of εd-N under different frequency loading
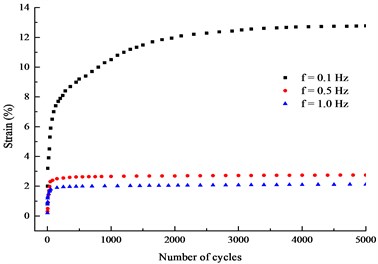
a) 200 kPa, 20 kPa
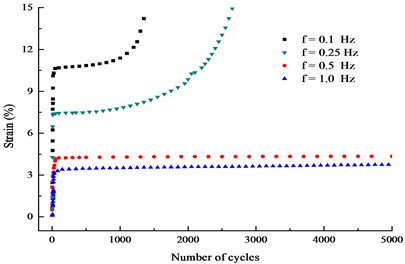
b) 200 kPa, 50 kPa
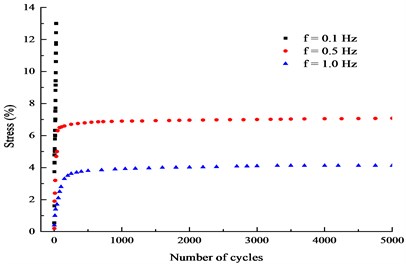
c) 250 kPa, 200 kPa, 65 kPa
1) The characteristic of plastic strain: the cumulative plastic strain and plastic strain growth rate decrease as loading frequency increases under isotropic consolidation or anisotropic consolidation with high cyclic stress or low cyclic stress condition. As shown in the Fig. 3(a), the cumulative plastic strain corresponding to the vibration frequency of 0.5 Hz was reduced by 77 % compared with 0.1 Hz; the cumulative plastic strain corresponding to 1 Hz was reduced by 23 % compared with 0.5 Hz under the cyclic load amplitude of 20 kPa. Fig. 3 indicates that the longer the time acting on the soil at low loading frequency, the greater the energy absorbed by the soil skeleton, and the greater the plastic strain caused.
2) The mode of plastic strain: The plastic strain developed at a higher growth rate when the cumulative plastic strain with a vibration frequency of 0.1 Hz belonged to the development type, while 0.5 Hz and 1 Hz were stable type. As shown in Fig. 3(b), both 0.1 Hz and 0.25 Hz are both destructive under cyclic stress of 50 kPa, and the cumulative plastic strain developed leaping in the later stage of the cycle. The growth rate increased sharply until the soil was destroyed, but when the loading frequency raise up to 0.5 Hz, the plastic strain developed stably with a small amount of strain.
3) Frequency threshold: between 0.25 Hz and 0.5 Hz, there was a frequency threshold, which made the development mode of cumulative plastic strain developed from stability to failure. As shown in Fig. 3(c), there was also a threshold frequency for the deviator consolidation. Once the loading frequency was lower than the threshold frequency, the cumulative plastic strain development mode would be abrupt.
(3) Characteristics of dynamic modulus.
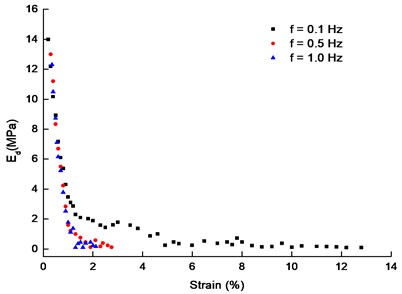
Fig. 4 presents the relationship between the dynamic elastic modulus and cumulative plastic strain under the same cyclic stress, but different frequencies, the isotropic consolidation (stress 200 kPa). The dynamic elastic modulus decays rapidly at the beginning, slowing down at the later stage, and gradually stabilizing.
Fig. 4Curves of Ed-εd under different frequency loading (σ1'=σ2'=σ3'= 200 kPa, σd= 20 kPa)
3.2. Influence of stress amplitude on dynamic deformation
(1) Characteristics of cumulative plastic strain.
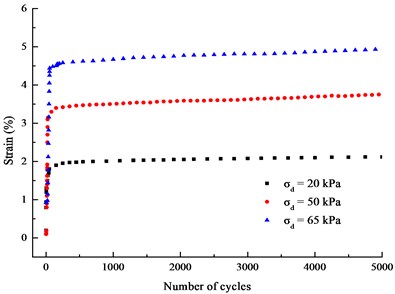
Fig. 5 presents the relationship between cumulative plastic strain and the number of cycles under the isotropic consolidation and the same frequency. As shown in Fig. 5, the cumulative plastic strain and the plastic strain rate increases cyclic stress increases during the loading frequency of 0.1 Hz to 1 Hz. The cumulative plastic strain increased by 75.88 % as the cyclic stress amplitude increased by 150 % (from 20 kPa to 50 kPa), and the cumulative plastic strain increased by 116 % as the cyclic stress amplitude increased by 30 % (from 50 kPa to 65 kPa) at the same vibration frequency. Results showed that the cumulative plastic strain of the muck soil increased nonlinearly with the dynamic stress and there was a critical dynamic cyclic stress. The strain increased sharply and the soil structure would be destroyed if the dynamic stress amplitude reached the critical value.
Fig. 5Curves of εd-N under different stress amplitude (σ1'=σ2'=σ3'= 200 kPa, f= 1 Hz)
(2) Characteristics of dynamic modulus.
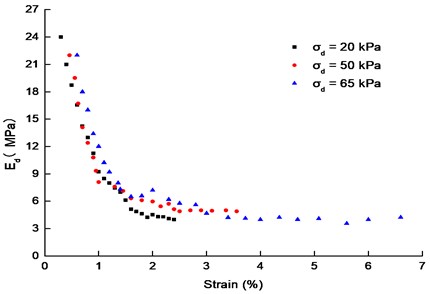
As showed in Fig. 6, the dynamic modulus-plastic strain curves under different cyclic stress amplitudes have similar trend. With the increasing of plastic strain, the dynamic elastic modulus reduced rapidly at the initial stage of loading, and linearly decreased greatly with the cumulative plastic strain. As the amplitude of the stress increased, the dynamic elastic modulus reduced with an increasing trend. As the magnitude of the stress increased, the energy of the impact would increase, the more energy was absorbed by the soil specimen, the easier the soil skeleton was destroyed, and the faster the dynamic elastic modulus reduced. The difference of the dynamic elastic modulus caused by the stress amplitude was small at the frequency of 0.1 Hz, while the effect of the dynamic stress amplitude on the dynamic elastic mode was more obvious when the frequency was greater than 1 Hz.
Fig. 6Curves of Ed-εd under different loading amplitude (σ1'=σ2'= 250 kPa, σ3'= 200 kPa, f= 0.5 Hz)
3.3. Influence of solid pressure on dynamic deformation
(1) Characteristics of cumulative plastic strain.
Fig.7 presents the relationship between the cumulative plastic strain and the number of cycles under different intermediate principal stresses for the same loading frequency and stress amplitude.
Fig. 7Curves of εd-N (f= 0.1 Hz, σd= 20 kPa)
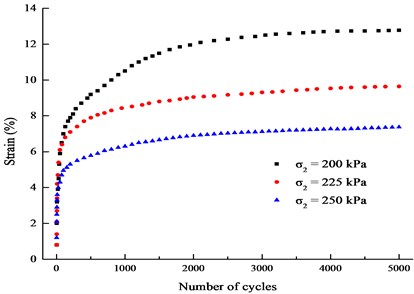
As shown in Fig. 7, the larger the intermediate principal stress developed, the smaller the final value of the cumulative plastic strain at the same cyclic stress and loading frequency would be. This was because the soil structure becomes tight and the stiffness of the muck increased as the consolidation stress increased, the ability to resist elastic deformation become strong. Results showed that under the low-frequency cyclic loading (0.1 Hz-1 Hz), the cyclic stress had no obvious plastic cumulative deformation of the muck, and the frequency influence was more significant.
(2) Characteristics of dynamic modulus.
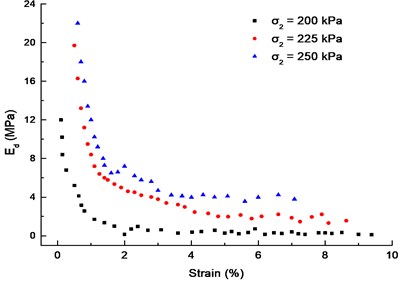
Fig. 8 presents the relationship between dynamic elastic modulus and the cumulative plastic strain under different medium principal stresses. As shown in Fig. 8, the trend of the dynamic elastic modulus of the muck decreased with the increasing of the plastic strain was similar. The curve was divided into three stages: rapid decline stage ( ≤ 2 %), slow decline stage (2 % < < 3 %), and gradual stabilization stage ( > 3 %). The dynamic elastic modulus increased as the consolidation stress under certain plastic strain condition. In addition, the dynamic elastic modulus decreased more slowly in the isotopically consolidated soil than the deviator consolidated soil under the same consolidation pressure. It showed that the consolidation stress was an important factor affecting the dynamic elastic modulus.
Fig. 8The curves of Ed-εd (f= 0.5 Hz, dynamic stress σd= 65 kPa)
4. Development model of dynamic elastic modulus
In summary, the vibration frequency and cyclic stress amplitude are not the most important factors affecting on dynamic elastic modulus under low-frequency traffic loads. The consolidation stress is more significant than the influence, and the dynamic elastic modulus of muck declines exponentially with plastic strain.
According to experimental data, taking the consolidation ratio as the parameter of model, a dynamic elastic modulus-exponential function relationship model was established. It can be expressed as:
where is the dynamic elastic modulus, is dynamic strain, and is consolidation ratio ( is the ratio of intermediate principal stress to minimum principal stress); , , , and are parameters of model, and is a fitting coefficient.
Fig. 9The comparison of Ed between experiment results and predicted values
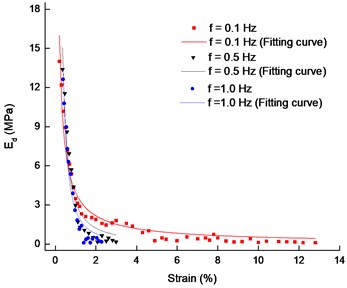
a) 200 kPa, 20 kPa
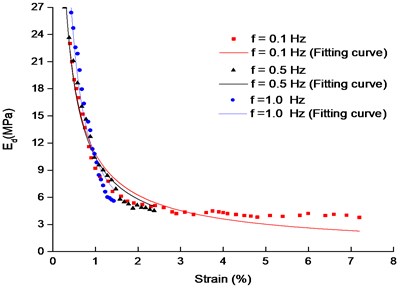
b) 250 kPa, 200kPa, 20 kPa
Fig. 9 shows that the experimental results of the dynamic elastic modulus were basically fitted to the calculated values of the model. Most of the fitting coefficients in Table 2 are greater than 0.92, indicating that the model can calculate accurately the dynamic elastic modulus under the low frequency loading, and it can describe the dynamic elastic modulus characteristics of muck soil.
Table 2Model parameters of dynamic elastic modulus
Dynamic stress (kPa) | Intermediate principal stress (kPa) | Frequency (Hz) | Model parameters | ||||
20 | 200 | 0.1 | 1.97027 | 1.970 | –0.435 | –0.435 | 0.962 |
20 | 200 | 0.5 | 1.3349 | 1.335 | –0.706 | –0.706 | 0.932 |
20 | 200 | 1.0 | 1.12513 | 1.125 | –0.850 | –0.850 | 0.948 |
20 | 200 | 0.1 | 2.54933 | 2.549 | –0.401 | –0.505 | 0.983 |
50 | 200 | 0.5 | 3.29101 | 3.291 | –0.821 | –0.821 | 0.967 |
50 | 200 | 1.0 | 2.01765 | 2.018 | –0.935 | –0.027 | 0.910 |
50 | 200 | 0.1 | 0.75414 | 0.754 | –0.474 | –0.474 | 0.968 |
65 | 200 | 0.5 | 1.03933 | 1.039 | –0.384 | –0.384 | 0.967 |
65 | 200 | 1.0 | 1.2878 | 1.288 | –0.597 | –0.597 | 0.926 |
65 | 200 | 0.1 | 5.27205 | 4.697 | –0.359 | –0.295 | 0.924 |
20 | 200 | 0.5 | 4.97836 | 4.436 | –0.490 | –0.419 | 0.973 |
20 | 200 | 1.0 | 3.33597 | 2.976 | –0.782 | –0.447 | 0.958 |
20 | 225 | 0.1 | 5.22578 | 4.656 | –0.359 | –0.195 | 0.940 |
50 | 225 | 0.5 | 5.77997 | 5.149 | –0.504 | –0.435 | 0.953 |
50 | 225 | 1.0 | 4.87879 | 4.348 | –0.856 | 0.003 | 0.950 |
50 | 225 | 0.1 | 4.33949 | 3.868 | –0.521 | –0.227 | 0.946 |
65 | 225 | 0.5 | 4.67348 | 4.165 | –0.485 | –0.443 | 0.978 |
65 | 225 | 1.0 | 4.19118 | 3.737 | –0.580 | –0.520 | 0.972 |
20 | 250 | 0.1 | 5.39062 | 4.333 | –0.541 | –0.200 | 0.961 |
20 | 250 | 0.5 | 4.68343 | 3.767 | –0.973 | 0.090 | 0.962 |
20 | 250 | 1.0 | 4.74175 | 3.813 | –0.801 | –0.297 | 0.949 |
20 | 250 | 0.1 | 6.92973 | 5.564 | –0.401 | –0.086 | 0.946 |
50 | 250 | 0.5 | 5.27237 | 4.238 | –0.580 | –0.257 | 0.951 |
50 | 250 | 1.0 | 5.64352 | 4.535 | –0.469 | –0.322 | 0.978 |
65 | 250 | 0.1 | 5.80641 | 4.665 | –0.331 | –0.089 | 0.936 |
65 | 250 | 0.5 | 6.27604 | 5.041 | –0.881 | –0.016 | 0.938 |
65 | 250 | 1.0 | 5.46557 | 4.392 | –0.497 | –0.412 | 0.971 |
5. Conclusions
Dynamic triaxial tests under different consolidation ratios, loading frequencies, and cyclic stress amplitudes were performed for 30 specimens of muck soil, and the dynamic deformation characteristics of muck soil under low frequency loading were as follows:
1) The energy of the loss increased as the stress amplitude, thus the area of the hysteresis loop and the length of the open section increase with the stress amplitude under the same cycle frequency and number of times. When the consolidation stress was large, the arrangement of the particles was tight, and the hysteresis loop entered the compact phase early, where the soil entered the elastic phase earlier.
2) The cumulative plastic strain of muck soil increased nonlinearly with the dynamic stress, and there existed a certain critical dynamic stress under the low-frequency cyclic loading. When the dynamic stress amplitude reached a critical value, the strain increased sharply, and the internal structure of the soil was destroyed. There existed a certain frequency threshold between 0.25 Hz and 0.5 Hz, and the cumulative plastic strain becomes failure mode from stability mode. With the increasing of the cyclic vibration, the stiffness of the muck gradually decreased, the plastic deformation produces and accumulates, and the lower the loading frequency, the greater the plastic deformation.
3) The dynamic elastic modulus of muck gradually decreased with the increasing of dynamic strain. During the initial loading phase, the dynamic elastic modulus declined rapidly with the dynamic strain, and then become slower and gradually stabilizes. The consolidation stress increased with the increasing of consolidation stress under low-frequency cyclic loading. The consolidation stress has a significant influence on the dynamic elastic modulus, while the vibration frequency and cyclic stress have weak influence. The empirical formulas of dynamic elastic modulus and plastic strain index were established with the consolidation stress ratio as the parameter, and the effectiveness was verified by the measured data. The results in this paper can provide theoretical basis for the establishment of muck soil dynamic constitutive model and structural dynamic response analysis.
References
-
Liu Y. J., Liu X. Q., Liu Y. H. A contrastive analysis of the physical and mechanical properties of soft soils in the Pearl River Delta. Journal of Guangdong University of Technology, Vol. 30, Issue 3, 2013, p. 30-36.
-
Liu Y. J., Li Z. M., Liang S. H. Neural network prediction of creep property of soft soils. Journal of Liaoning Technical University (Natural Science), Vol. 32, Issue 5, 2013, p. 607-610.
-
Huang J., Ding Z. D., Yuan T. Y., et al. Experimental study of dynamic deformation properties of peaty soil under cyclic loading. Rock and Soil Mechanics, Vol. 38, Issue 9, 2017, p. 2551-2558.
-
Zhang X. D., Liu J. S., Zhang H. W. Experimental study on dynamic characteristic of soft soil under cyclic loading. Journal of Highway and Transportation Research and Development, Vol. 31, Issue 5, 2014, https://doi.org/10.1061/JHTRCQ.0000407.
-
Wang J., Chen Z. L., Cai Y. Q. Study on dynamic stress-strain relationship of soft clay considering degradation of stiffness under cyclic loading. Journal of Zhejiang University (Engineering Science), Vol. 41, Issue 1, 2007, p. 23-29.
-
Hardin B. O., Drnevich V. P. Shear modulus and damping in soils: design equation curves. Journal of the Soil Mechanics and Foundations Division, Vol. 98, Issue 7, 1972, p. 279-287.
-
Hardin B. O., Black W. L. Closure to vibration modulus of normally consolidated clay: design equations and curves. Journal of the Soil Mechanics and Foundations Division, Vol. 95, Issue 6, 1969, p. 1531-1537.
-
Hardin B. O., Drnevich V. P. Shear modulus and damping in soil: measurement and parameter effects. Journal of the Soil Mechanics and Foundations Division, Vol. 98, Issue 6, 1972, p. 603-624.
-
Yashuara K., Yamanouchi T., Hirao K. Cyclic strength and deformation of normally consolidated clay. Soils and Foundations, Vol. 22, Issue 3, 1982, p. 77-91.
-
Yasuhara K., Murakami S., Song B. W. Pos tcyclic degradation of strength and stiffness for low plasticity silt. Journal of Geotechnical and Geo-environmental Engineering, Vol. 129, Issue 8, 2003, p. 756-769.
-
Boulanger R. W., Arulnathan R., Harder L. F., et al. Dynamic properties of Sherman island peat. Journal of Geotechnical and Geoenvironmental Engineering, Vol. 124, Issue 1, 1998, p. 12-20.
-
Wehling T. M., Boulanger R. W., Arulnathan R., et al. Nonlinear dynamic properties of a fibrous organic soil. Journal of Geotechnical and Geoenvironmental Engineering, Vol. 129, Issue 10, 2003, p. 929-939.
-
Lei H. Y., Jiang Y., Lu P. Y., et al. Experimental study of dynamic stress-strain relation of structural soft soil under traffic load. Chinese Journal of Rock Mechanics and Engineering, Vol. 27, 2008, p. 3052-3056.
-
Jiang Y., Lei H. Y., Zheng G. Deformation prediction of structured soft clay under cyclic load. Journal of Traffic and Transportation Engineering, Vol. 12, Issue 1, 2011, p. 13-18.
-
Liu S. C., Cao Y., Yang Z. W. Study on the deformation behavior of soft soil subgrade under dynamic load. Journal of Railway Engineering Society, Vol. 5, 2011, p. 22-26.
-
Fujikawa K. On Optimistic Design of Low Embankment Road on Soft Subsoil by Considering the Traffic-Load Induced Settlement. Saga University, Saga, 1996.
-
Chai J. C., Miura N. Traffic-load-induced permanent deformation of road on soft subsoil. Journal of Geotechnical and Geoenvironmental Engineering, Vol. 128, Issue 11, 2002, p. 907-916.
-
Idriss I. M., Dobry R., Singh R. D. Nonlinear behavior of soft clay s during cyclic loading. Journal of the Soil Mechanics and Foundations Division, Vol. 104, Issue 12, 1978, p. 1427-1447.
-
Lefebvre G., Pfendler P. Strain rate and preshear effects in cyclic resistance of soft clay. Journal of Geotechnical Engineering, Vol. 22, Issue 1, 1996, p. 21-26.
-
Zhang Y., Kong L. W., Guo A. G., et al. Cumulative plastic strain of saturated soft clay under cyclic loading. Rock and Soil Mechanics, Vol. 30, Issue 6, 2009, p. 1542-1548.
-
Wei X., Huang M. S. A simple method to predict traffic-load-induced permanent settlement of road on soft subsoil. Rock and Soil Mechanics, Vol. 30, Issue 11, 2009, p. 3342-3348.
-
Liu Y. H., Huang M. S., Li S. An anisotropic bounding surface model for structured soft clay under cyclic loading. Chinese Journal of Geotechnical Engineering, Vol. 32, Issue 7, 2010, p. 1065-1071.
-
Ding B. Y., Zhang Y. Discussion on dynamic test and characteristics of structural properties of quaternary soft clay in Hangzhou Region. Rock and Soil Mechanics, Vol. 33, Issue 2, 2012, p. 336-342.
-
Liu Y. J., Li Z. M., Guo L. F. Pore characteristics of soft soil under triaxial shearing measured with NMR. Chinese Journal of Rock Mechanics and Engineering, Vol. 37, Issue 8, 2018, p. 1924-1932.
-
Liu Y. J., Wu J. S., Xie Z. K. Experiment study on microstructure of soft soil in Nansha district based on NMR and SEM Test. Journal of Guangdong University of Technology, Vol. 35, Issue 6, 2018, p. 49-56.
About this article
The work reported here was supported by the National Natural Science Fund (No. 51178122) of P. R. China, the Natural Science Fund (No. 2016A030313692, No. 2018A030313839) of Guangdong Province, P. R. China and the Science and Technology Plan Project of Guangdong Provincial Department of Transportation (No. 201702018).
Yongjian Liu designed the test plan, discussed theories of soil. Qiyang Luo conducted the dynamic properties test and theoretical study of soft soil. Xin Yang conducted experiments and analysis on the dynamic properties of soil. Bingxiang Yuan analyzed deformation properties of muck soil. Lan Luo analyzed the test data and edited the paper. Mingyang Lai discussed the physical and mechanics properties test of soft soil.
