Analysis on transformer vibration signal recognition based on convolutional neural network

3.1. Introduction of convolutional neural network

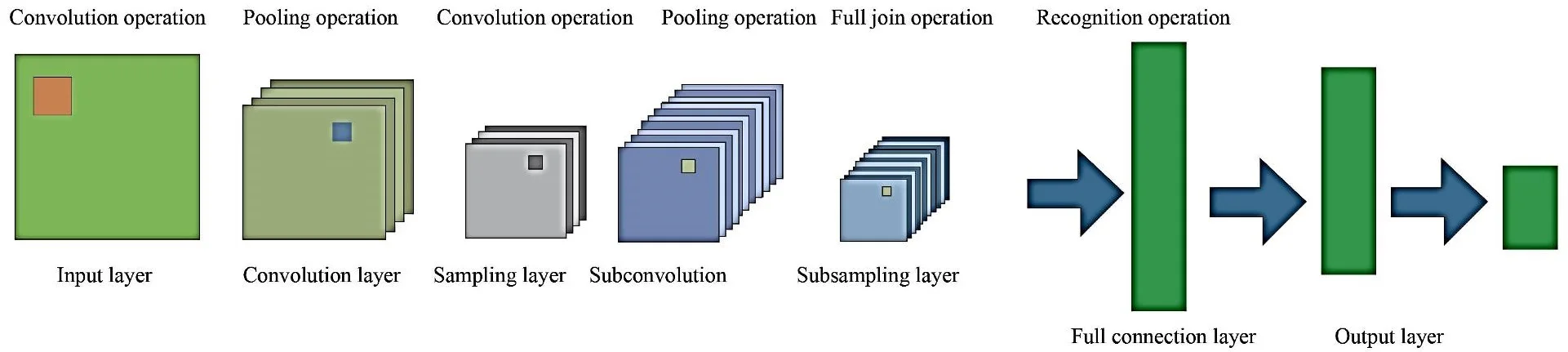
As shown in Fig. 1, the existing convolutional neural network structure includes the input layer, the intermediate hidden layer and the output layer. The intermediate hidden layer is composed of one or more convolutional layers and sampling layers. In the basic structure of a convolutional neural network, the components that are mainly used to extract features are the convolutional layer, sampling layer and fully connected layer.

Fig. 1Structure diagram of convolutional neural network

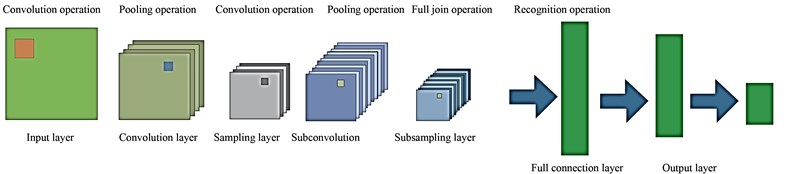
Convolutional Layer: The convolutional layer is mainly used for feature extraction, which is to extract local features of each neuron and then serve as the output neuron of the layer. It is mainly through the sparse connection of neurons at the input layer and network weights, and then two-dimensional convolution, the local features of neurons can be obtained, and the relationship between other features can be determined based on this feature information.

Sampling Layer: This layer is used in the Convolutional Neural Network for intermediate sampling of output features provided by the convolutional layer. Feature information, which is obtained by convolution layer to feature mapping requires by sampling, the convolution output layer neurons as sampling the input layer, similar to the process of convolution layer, layer of sample has multiple features in the process of mapping, in the sample layer each feature mapping plane all the neurons have the same weight, sampling for the input image in convolution layer in convolution summation, and bias, after a sigmoid function which is to get the output of the sample layer [31]. In feature mapping, the excitation function Sigmoid with small kernel of influence function is used to obtain the mapping feature with constant displacement. In the sampling layer, all neurons in the plane of each feature map have the same weight, thus reducing the computational complexity of the network. The structure with sampling layer is connected behind the convolutional layer, which can make the feature mapping extracted by the convolutional layer more concentrated.

Fully Connected Layer: This acts as a traditional neural network that extracts the feature vector from the adjacent subsampling layers and provide the output probabilities to the final output layer of the network. The output probabilities are obtained using the softmax activation function at the output layer that yields the probability values ranging from 0 to 1 indicating the categorical output classes.

In this work, the input provided to the convolutional neural network contain 3600 images extracted by the time-frequency transform method of wavelet transform. The output of the convolutional network provides the vibration fault analysis into three different fault classes namely; the inner race (IR) fault, the outer race (OR) fault and the rolling bearing (BA) faults. The analysis was done on the vibration signal under different motor loads and fault diameters to yield three-class classification using the CNN network into IR faults, BA faults and OR faults.

3.2. Wavelet transform

Wavelet transform solves the contradiction in time-frequency domain very well. It is not only a local transform in time, but also a local transform in frequency domain. Wavelet transform can be used to make a more detailed analysis of the frequency of function or signal by means of expansion, translation and other operational functions, and solve many difficult problems that cannot be solved by Fourier transform to a great extent. The wavelet transform is formed by scaling and shifting the parent wavelet function. A signal $x\left(t\right)$ is a signal with limited energy, which satisfies:

Its wavelet transform is defined as the integral transform with the function cluster ${\mathrm{\Psi }}_{a,\tau }\left(t\right)$ as the integral kernel, as follows:

Function cluster ${\mathrm{\Psi }}_{a,\tau }\left(t\right)$ is the wavelet function cluster generated by basic wavelet function $\mathrm{\Psi }\left(t\right)$ through expansion and translation:

where, $A$ is the scale parameter, $\tau$ is the time shift parameter, and $1/\sqrt{a}$ is the normalized constant to ensure the energy conservation of the transformation, namely:

It can be seen from the above formula that the wavelet transform is A linear transformation, which USES the oscillation function ${\mathrm{\Psi }}_{a,\tau }\left(t\right)$ as the window to scan and shift the signal $X\left(t\right)$ by changing the frequency, where the expansion parameter used to change the oscillation frequency is a and the translation parameter is $\tau$. Unlike THE STFT, the wavelet transform can change the resolution in time domain and frequency domain by adjusting the frequency. In high frequency band, wavelet transform can achieve good time domain resolution, but the frequency domain resolution is poor, in low frequency band, the situation is just the opposite.

3.3. Test objects

In order to conduct the research on transformer vibration identification, a transformer model sfSZ10-180,000 /220 is selected as the research object. The specific parameters are shown in Table 1.

3.4. Vibration test

In the process of acquisition, the acceleration sensor of six models for ULT2008 separately adsorbed on the surface of the test transformer tank is utilized. The high side and low voltage side, the location of the points is shown in Fig. 2. Among them, 1, 2, 3 points located on the high side, 4, 5, 6 point located in the low voltage side. At the same time, the model for ULT2061 adsorption three-dimensional vibration acceleration sensor is used in the test transformer. A phase (point 1) level of 10 cm is used to the right direction; where $X$ direction is the horizontal direction, $Y$ direction is the vertical direction and the $Z$ direction represents the direction perpendicular to the surface of the transformer.

In Fig. 2; A, B, C indicates the three-dimensional points at the high voltage side and a, b, c indicates the three-dimensional points at the low voltage side. The surface vibration signal of transformer contains abundant state information, and whether the measured signal collected is complete and effective has an important influence on the feature extraction of vibration signal and the status evaluation of transformer. The image of a real-life transformer is depicted in Fig. 3.

The real-life transformer is completely different and complex comparative to its schematic diagram. Due to the complex transformer structure and the influence of transmission path and other factors, the unreasonable setting of sampling frequency and sampling length in the signal acquisition process is likely to lead to the large difference in vibration signal characteristics. This condition collected by the same transformer seriously affects the analysis and judgment of transformer operating state [32, 33]. Therefore, in the process of collecting the transformer surface vibration data, the following parameters are mainly set:

Sampling frequency, FS: Setting a reasonable sampling frequency can effectively avoid signal distortion. Relevant studies have shown that the transformer vibration signal is mainly within 1 kHz. According to the sampling theorem, the sampling frequency should be no less than 2 kHz.

Sampling interval, $T$: It refers to a length t (sampling length) sampling of the transformer at a certain time interval. The setting of this parameter should be in the same period of time with the operating condition data of the transformer, such as operating voltage, load current and oil tank, so as to facilitate the analysis of data of different working conditions. It is found through field investigation that the transformer substation records the operating condition data every 5 minutes when monitoring the transformer, so it is recommended to set this parameter to 5 minutes.

Sampling time, $T$: It refers to the time required to complete $f=1/T$, sampling, which is related to frequency to some extent. The smaller the sampling length is, the smaller the frequency interval will be, and the higher the frequency resolution will be, namely, $f=1/T$. Therefore, this parameter can be set according to the minimum frequency to be studied when analyzing the vibration signal.

To sum up, according to the actual requirements of transformer vibration signal analysis in this paper, relevant parameters of data acquisition are set as follows: sampling frequency 10 kHz, sampling duration 1 s, and sampling interval 5 min.

Fig. 2Schematic diagram of measuring points for the vibration test

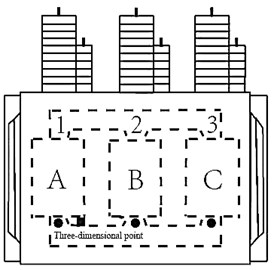
a) High voltage side

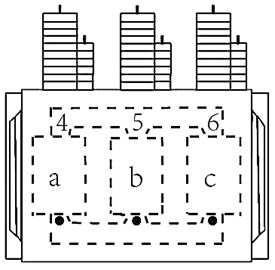
b) Low voltage side

Fig. 3Real-life transformer

4.1. Sample data

The samples used in this paper were divided into a section every 0.05 s of the data of each measurement point, and 3600 sections were taken for wavelet transform analysis of each section of data to obtain the time-frequency diagram of the vibration signal of this section. The training samples were set as training samples, so the training samples were divided into 9 groups with 3600 samples in each group and a total of 32,400 samples in the training sample set [34, 35]. 400 segments of data are taken after a period of time, and wavelet transform is performed to obtain time-frequency graph, which is set as the test sample. Similarly, the test samples were divided into 9 groups of 400 for a total of 3,600. The time-frequency graphs of different measurement points are shown in Fig. 4 form both normal and faulty condition.

Fig. 4a) Normal bearing signal, c) faulty bearing signal; time-frequency diagram of the measuring point of Phase A on the high-pressure side of the transformer for b) normal bearing signal and d) faulty bearing signal

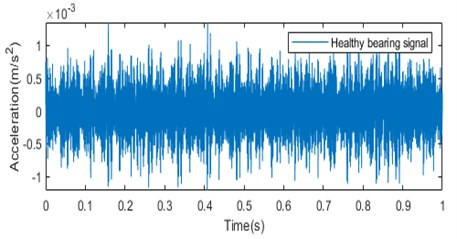
a)

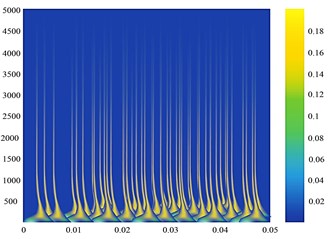
b)

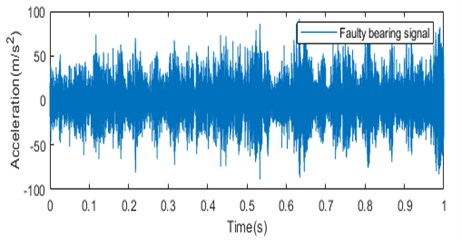
c)

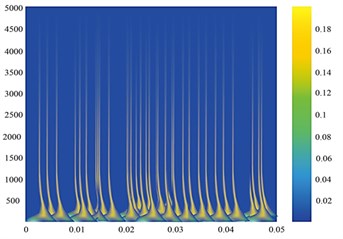
d)

The time-frequency diagram is fed to the CNN network. The images extracted by the time-frequency transform method of wavelet transform can effectively represent the localization characteristics of the original signal frequency and contain rich state information. The information depicted by the time-frequency diagram shows that the amplitude of the signal is larger in case of faulty condition than in the normal condition. The color variation in the wavelet transform output depicts the magnitude of the time-frequency grid coefficients. The wavelet transforms outputs carry very important information regarding the faulty condition as the high energy peaks indicated in the wavelet transform outputs at the low frequency bands provides the information about the bearing that is heading to the defect or faulty condition. These images are provided to the CNN network for classification of vibration faults into three types; IR faults, BA faults and OR faults.

4.2. Verification of transformer vibration signal results

The deep learning framework Caffe was used to construct the convolutional neural network. Set the batch number of each batch to 64, that is, each batch can handle 64 samples. Since there are 32,400 samples, 507 batches shall be processed after all the samples are processed. The number of iterations was set as 10, and an iteration was a training for the entire training sample set. Therefore, the maximum number of iterations was set as 550, and a total of 5500 training sessions were required for 10 iterations.

The confusion matrix obtained for three class classification of vibration signal into IR faults, OR faults and BA faults is depicted in Table 2.

The confusion matrix depicts the difference in the actual fault labels and the predicted labels in terms of true positives (TP), true negatives (TN), false positives (FP) and false negatives (FN). The training effect of the convolutional network is evaluated in terms of accuracy, sensitivity, specificity, positive prediction rate and the loss function, which are provided by Eq. (5-9):

where $TP$ – true positive, $TN$ – true negative, $FP$ – false positive, $FN$ – false negative, $M$ – class, $t$ – true classification, $o$ – observation, $p$ – prediction probability and $y$ – binary indicator for correct class label.

Loss function can also be referred to as the cost function, is the objective function in the process of neural network is optimized, or optimization of neural network training is the ultimate goal is to minimize the Loss function, that is to say, Loss function value is smaller, the corresponding prediction results and the real situation is closer to, this paper uses the Loss function of Softmax-With-Loss, a network model for Caffenet.

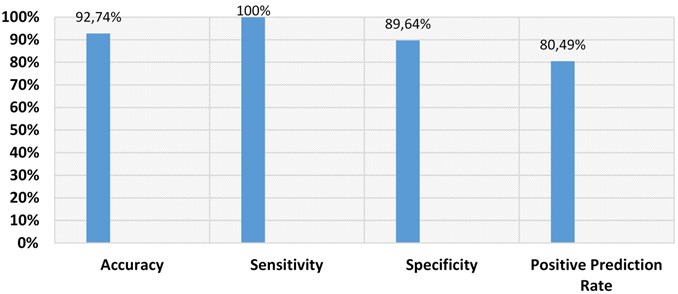
The performance of convolutional neural network is evaluated in terms of different parameters like sensitivity, specificity, accuracy and positive prediction value. The outcomes obtained are tabulated in Table 3 and are graphically represented in Fig. 5.

Table 3 and Fig. 5 depicts values of the performance evaluation parameters for the convolutional neural network classification outcomes obtained. It provides the accuracy value of 92.74 % while providing sensitivity of 100 %, specificity of 89.64 % and positive prediction rate of 80.49 %.

From Fig. 5, the sensitivity rate of 100 % reveals that the convolutional network is fully capable of identifying the true faulty vibration signal pixels.

Fig. 5Performance evaluation parameters for classification outcomes

The relationship between the accurate recognition rate and loss function of the test set and the number of iterations is shown in Fig. 6. The specific values are shown in Fig. 6.

Fig. 6Curve of a) accurate recognition rate and iteration times of test set b) loss function and iteration times curve of test set

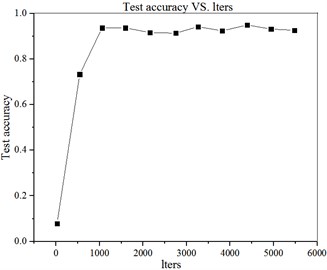
a)

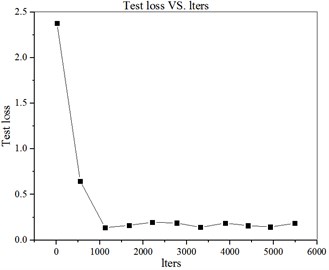
b)

The accuracy curve computations for convolutional neural network are provided in Fig. 7. This depicts the increase in the accuracy rate for the increasing iterations from 0 to 10 while increasing the samples from 0 to 5500 with the 550 step increment.

It can be seen from Fig. 6 and Fig. 7 that in the first two iterations, the accuracy of the test set increases steadily and rapidly, and the loss function declines rapidly. After two iterations, the accuracy rate and the loss value remain in a relatively stable state, indicating that the sample data can be trained to converge under the model and parameters.

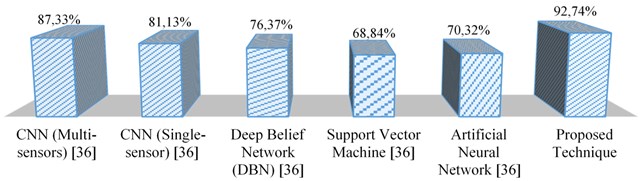
The comparative analysis of the proposed technique with the other state-of-the-art methods are depicted in Fig. 8.

From Fig. 8, it is revealed that the proposed approach outperforms the other state-of-the-art methods in vibration signal recognition, thereby providing the maximum accuracy of 92.74 % comparative to the other existing approaches.

Combined with the analysis results can be seen that the method can accurately identify different measuring point of the signal, the vibration signal has good recognition effect, proved that the method of surface vibration signals of transformer classification is feasible, but the recognition accuracy is associated with the set of convolution network model parameters, still need to through the experiment many times to adjust the network parameters in the model, in order to achieve the best recognition rate.

Fig. 7Iteration times and test set accuracy

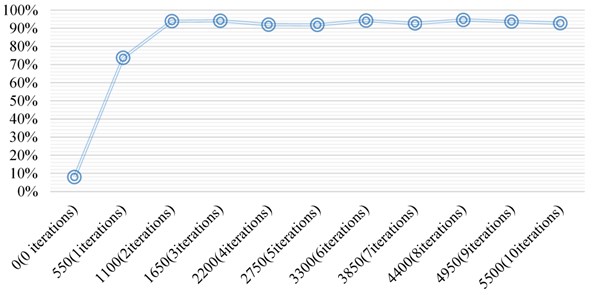
Fig. 8Comparative analysis of the proposed technique with state-of-the-art methods