Vibration characteristics analysis of face gear transmission system considering gyroscopic effect

Li, Xiaozhen; Su, Kuo; Li, Tongjie; Zhang, Liyong

doi:10.21595/jve.2022.22289

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 June 2022

Check for updates

Vibration characteristics analysis of face gear transmission system considering gyroscopic effect

Xiaozhen Li¹

Kuo Su²

Tongjie Li³

Liyong Zhang⁴

¹College of Mechanical Engineering, Jiangsu University, Zhenjiang, Jiangsu, 212013, China

^{1, 2, 3, 4}College of Mechanical Engineering, Anhui Science and Technology University, Chuzhou, Anhui, 233100, China

Corresponding Author:

Xiaozhen Li

Cite the article Download PDF

Downloads 573

Abstract

To improve the dynamics of the face gear transmission system, a nonlinear dynamics model considering gyroscopic effects and including parameters such as time-varying meshing stiffness, meshing damping, tooth side clearance, support stiffness and damping is developed. The Runge-Kutta method was used to solve the nonlinear kinetic equations and analyze the accuracy and reasonableness of the model calculation results. The vibration displacement, vibration velocity and vibration acceleration along each direction of the face gear and straight cylindrical gear were analyzed, and the torsional vibration characteristics of the center of mass of the two gears were studied.

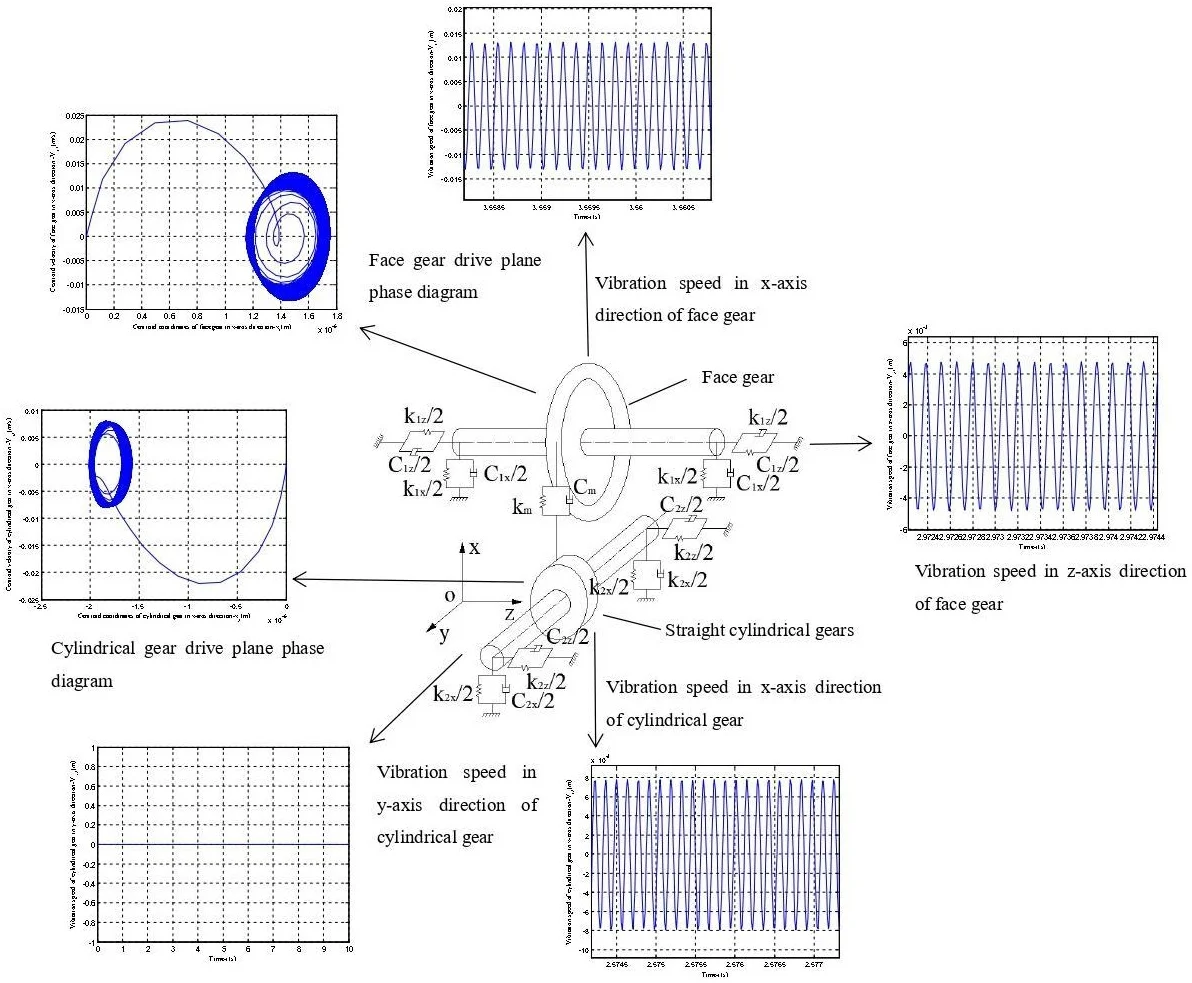
Vibration characteristics analysis of face gear transmission system considering gyroscopic effect

Highlights

The dynamics of the orthogonal face gearing system is modeled, and the gyroscopic effect of the gears around their centers of mass during the face gearing process is considered in the model.
The dynamical equations in the paper are solved using the Eulerian single-step method to analyze the nonlinear dynamical vibration characteristics of the face gearing system considering the gyroscopic effect.
In this paper, the gyroscopic effect is considered and the vibration response of each degree of freedom of the gearing opposite to each parameter is analyzed.

1. Introduction

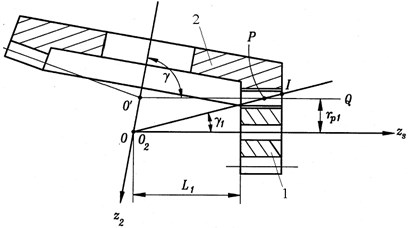
Face gear transmission is a cylindrical gear and bevel gear meshing gear transmission, its transmission principle is shown in Fig. 1, where the gear 1 for the involute straight cylindrical gear, gear 2 for the bevel gear, two-wheel axis intersection, its angle is $γ$ . When the axis intersection angle $γ =$ 90 °, the bevel gear teeth will be distributed in a circular plane, the bevel gear is the face gear, and thus generally known as the face gear transmission.

Fig. 1Face gear transmission

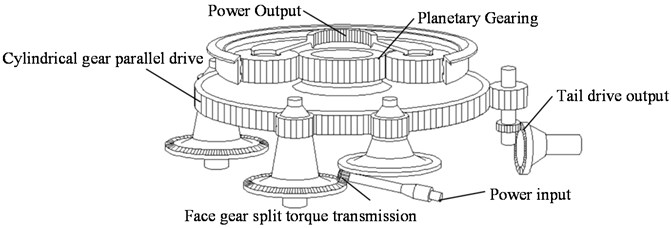
Face gears have the advantages of low vibration, low noise, high load-bearing capacity and simple structure [1-5]. In the ART program jointly carried out by the US. military and NASA in the 1990s, a new helicopter main gear using face gears for split-torsion transmission was designed, and face gears were used as the mechanism for split-torsion transmission in the main gear [6]. As shown in Fig. 2, the power output from the engine is shunted to two face gears by a cylindrical gear to realize the split-torsion transmission. Compared with the traditional helicopter main gear using bevel gear as the split-torsion transmission mechanism, the split-torsion transmission mechanism with face gear has a simple support structure and a weight reduction of about 40 %, and its power shunting effect is better, with less vibration and lower noise, which has obvious advantages over the bevel gear split-torsion transmission.

Fig. 2Helicopter main gearbox with face gear split-torsion drive

The current study of the dynamics of face gearing systems mainly uses the centralized parameter method [7-10],establishment of a bending-torsional coupled nonlinear dynamics model for an orthogonal gear train with time-varying meshing stiffness, meshing damping, tooth surface error, tooth surface friction, tooth side clearance, bearing clearance and other factors [11-15], solving the system of kinetic differential equations using the Runge-Kutta method, obtain the nonlinear vibration characteristics of the system and the influence of various parameters on the dynamic characteristics of the system, the swing of the two gears around their center of mass is not considered in the model [16-20]. In this paper, the dynamics of the face gear transmission system is modeled considering the gyroscopic effect. The influence of various parameters on the vibration of various degrees of freedom in face gear transmission system is analyzed, the model built is closer to the actual vibration of the face gear drive.

High speed is a trend of modern rotating machinery, and in the case of high speed, the gyroscopic effect cannot be ignored [21]. The gyroscopic effect is a physical phenomenon that occurs when the orientation of the symmetry axis of the rotor changes in high-speed rotating machinery. When the symmetry axis of the rotor is forced to change its orientation in space, that is, when the symmetry axis is forced to move, the rotor must act on the bearing an additional force couple, this phenomenon is the gyroscopic effect. The gyroscopic effect affects both the critical speed and stability of the rotor. To ensure safe and reliable operation of the machinery, it is necessary to consider the effect of the gyroscopic effect on rotor vibration [22]. The face gears studied in this paper are orthogonal face gears, and the face gears mentioned below all refer to orthogonal face gears.

2. System dynamics modeling

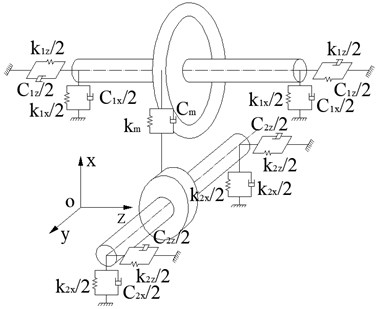
By using centralized parameters, the dynamic model of the orthogonal gear transmission system considering the gyro effect is established as shown in Fig. 3. The inertial coordinate system $o$ - $x y z$ belongs to the right-handed spiral coordinate system. When the gear is in a stationary state, the coordinate axis $o y$ is parallel to the rotation axis of the driving straight cylindrical gear 2, and the coordinate axis $o z$ is parallel to the rotation axis of the driven surface gear 1. Face gears and straight cylindrical gears are regarded as concentrated masses. The supports at both ends of the two gears are treated as elastic supports, and their support forms are treated as massless springs and dampers.

In order to study the dynamic characteristics of the orthogonal face gear transmission system, the dynamic coordinate systems $o_{1}$ - $x_{1} y_{1} z_{1}$ and $o_{2}$ - $x_{2} y_{2} z_{2}$ fixedly connected with the face gear and the straight cylindrical gear were established respectively, the coordinate origin $o_{1}$ and $o_{2}$ of the two-movement coordinate system are respectively at the center of mass of the face gear and the straight cylindrical gear. When the two gears are at rest, the coordinate axes of the moving coordinate system are parallel to the corresponding coordinate axes of the inertial coordinate system $o$ - $x y z$ which is:

\begin{array}{l} o x | | o_{1} x_{1}, o y | | o_{1} y_{1}, o z | | o_{1} z_{1}, \\ o x | | o_{2} x_{2}, o y | | o_{2} y_{2}, o z | | o_{2} z_{2} . \end{array}

Fig. 3Dynamic model of face gear transmission system

During the transmission of the face gear, the load on the face gear 1 can be decomposed into the axial component force parallel to the $o_{1} z_{1}$ axis and the tangential component force parallel to the $o_{1} x_{1}$ axis. Therefore, the center of mass o₁ of the face gear 1 can freely vibrate in a plane parallel to the coordinate plane $o x z$ , and can rotate on a fixed axis relative to the center of mass $o_{1}$ , so the face gear 1 has two translational degrees of freedom and three rotational degrees of freedom. The force analysis of the face gear 1 is carried out. It is subjected to the reaction force ${\vec{F}}_{e}^{1}$ and the reaction moment ${\vec{M}}_{e}^{1}$ of the shaft 1, and the reaction force ${\vec{F}}_{n}^{1}$ and the reaction moment ${\vec{M}}_{n}^{1}$ of the straight cylindrical gear 2 to the face gear 1 (ignoring the friction between the tooth surfaces). According to the momentum theorem of the center of mass and the momentum moment theorem around the center of mass $o_{1}$ , we get:

1

m_{1} \frac{d^{2} {\overset{⃑}{r}}_{o 1}}{d t^{2}} = {\overset{⃑}{F}}_{e}^{1} + {\overset{⃑}{F}}_{n},

2

{\overset{⃑}{J}}_{1} \cdot \frac{\tilde{d} {\overset{⃑}{ω}}_{1}}{d t} + {\overset{⃑}{ω}}_{1} \times {\overset{⃑}{J}}_{1} \cdot {\overset{⃑}{ω}}_{1} = {\overset{⃑}{M}}_{e}^{1} + {\overset{⃑}{M}}_{n}^{1} .

where $m_{1}$ is the mass of the face gear 1; ${\overset{⃑}{r}}_{o 1}$ is the vector diameter of the face gear 1 center of mass with respect to the origin o of the inertial coordinate system, and its projection expression in the inertial coordinate system is $(x_{o 1}, y_{o 1}, z_{o 1})$ ; ${\overset{⃑}{J}}_{1}$ is the inertia tensor of the face gear with respect to the dynamic coordinate system $o_{1}$ - $x_{1} y_{1} z_{1}$ , and its inertia matrix expression in the dynamic coordinate system $o_{1}$ - $x_{1} y_{1} z_{1}$ , considering the symmetry of the gear, is:

3

{\overset{⃑}{J}}_{1} = [\begin{matrix} J_{x_{1}}^{1} & 0 & 0 \\ 0 & J_{y_{1}}^{1} & 0 \\ 0 & 0 & J_{z_{1}}^{1} \end{matrix}],

where ${\overset{⃑}{ω}}_{1}$ is the angular velocity of the face gear 1, which is also the angular velocity of the dynamic coordinate system $o_{1}$ - $x_{1} y_{1} z_{1}$ with respect to the inertial coordinate system $o$ - $x y z$ , and its component expression in the dynamic coordinate system is $(ω_{x_{1}}^{1}, ω_{y_{1}}^{1}, ω_{z_{1}}^{1})$ . The reaction moment ${\overset{⃑}{M}}_{n}^{1}$ is the moment of the reaction force ${\overset{⃑}{F}}_{n}$ on the center of mass $o_{1}$ .

The expressions for the components of ${\overset{⃑}{F}}_{e}^{1}$ and ${\overset{⃑}{F}}_{n}$ in the inertial coordinate system are:

4

{\overset{⃑}{F}}_{e}^{1} = (F_{e}^{1 x}, F_{e}^{1 y}, F_{e}^{1 z}),

5

{\overset{⃑}{F}}_{n} = (F_{n}^{x}, F_{n}^{y}, F_{n}^{z}) .

The expressions for the components of ${\overset{⃑}{M}}_{e}^{1}$ and ${\overset{⃑}{M}}_{n}^{1}$ in the dynamic coordinate system $o_{1}$ - $x_{1} y_{1} z_{1}$ are:

6

{\overset{⃑}{M}}_{e}^{1} = (M_{e}^{1 x_{1}}, M_{e}^{1 y_{1}}, M_{e}^{1 z_{1}}),

7

{\overset{⃑}{M}}_{n}^{1} = (M_{n}^{1 x_{1}}, M_{n}^{1 y_{1}}, M_{n}^{1 z_{1}}) .

Rewriting Eqs. (1) and (2) into scalar form, the kinematic equation of the face gear 1 is obtained as:

8

m_{1} \frac{d^{2} x_{o 1}}{d t^{2}} = F_{e}^{1 x} + F_{n}^{x},

9

m_{1} \frac{d^{2} z_{o 1}}{d t^{2}} = F_{e}^{1 z} + F_{n}^{z},

10

J_{x_{1}}^{1} {\dot{ω}}_{x_{1}}^{1} + (J_{z_{1}}^{1} - J_{y_{1}}^{1}) ω_{y_{1}}^{1} ω_{z_{1}}^{1} = M_{e}^{1 x_{1}} + M_{n}^{1 x_{1}},

11

J_{y_{1}}^{1} {\dot{ω}}_{y_{1}}^{1} + (J_{x_{1}}^{1} - J_{z_{1}}^{1}) ω_{z_{1}}^{1} ω_{x_{1}}^{1} = M_{e}^{1 y_{1}} + M_{n}^{1 y_{1}},

12

J_{z_{1}}^{1} {\dot{ω}}_{z_{1}}^{1} + (J_{y_{1}}^{1} - J_{x_{1}}^{1}) ω_{x_{1}}^{1} ω_{y_{1}}^{1} = M_{e}^{1 z_{1}} + M_{n}^{1 z_{1}} .

Using the Eulerian parameter $(λ_{0}^{'}, λ_{1}^{'}, λ_{2}^{'}, λ_{3}^{'})$ to describe the orientation of face gear 1 with respect to the inertial coordinate system, the kinematic equation of face gear 1 is:

13

\{\begin{array}{l} 2 {\dot{λ}}_{0}^{'} = - ω_{x_{1}}^{1} λ_{1}^{'} - ω_{y_{1}}^{1} λ_{2}^{'} - ω_{z_{1}}^{1} λ_{3}^{'}, \\ 2 {\dot{λ}}_{1}^{'} = ω_{x_{1}}^{1} λ_{0}^{'} + ω_{z_{1}}^{1} λ_{2}^{'} - ω_{y_{1}}^{1} λ_{3}^{'}, \\ 2 {\dot{λ}}_{2}^{'} = ω_{y_{1}}^{1} λ_{0}^{'} - ω_{z_{1}}^{1} λ_{1}^{'} + ω_{x_{1}}^{1} λ_{3}^{'}, \\ 2 {\dot{λ}}_{3}^{'} = ω_{z_{1}}^{1} λ_{0}^{'} + ω_{y_{1}}^{1} λ_{1}^{'} - ω_{x_{1}}^{1} λ_{2}^{'} . \end{array}

The directional cosine matrix can be conveniently represented using Eulerian parameters:

14

A^{(1,0)} = [\begin{matrix} 2 [{(λ_{0}^{'})}^{2} + {(λ_{1}^{'})}^{2}] - 1 & 2 (λ_{1}^{'} λ_{2}^{'} + λ_{0}^{'} λ_{3}^{'}) & 2 (λ_{1}^{'} λ_{3}^{'} - λ_{0}^{'} λ_{2}^{'}) \\ 2 (λ_{1}^{'} λ_{2}^{'} - λ_{0}^{'} λ_{3}^{'}) & 2 [{(λ_{0}^{'})}^{2} + {(λ_{2}^{'})}^{2}] - 1 & 2 (λ_{2}^{'} λ_{3}^{'} + λ_{0}^{'} λ_{1}^{'}) \\ 2 (λ_{1}^{'} λ_{3}^{'} + λ_{0}^{'} λ_{2}^{'}) & 2 (λ_{2}^{'} λ_{3}^{'} - λ_{0}^{'} λ_{1}^{'}) & 2 [{(λ_{0}^{'})}^{2} + {(λ_{3}^{'})}^{2}] - 1 \end{matrix}] .

A similar equation is obtained by the same analysis of straight cylindrical gear 2, corresponding to Eqs. (1) and (2):

m_{2} \frac{d^{2} {\overset{⃑}{r}}_{o 2}}{d t^{2}} = {\overset{⃑}{F}}_{e}^{1} - {\overset{⃑}{F}}_{n},

{\overset{⃑}{J}}_{2} \cdot \frac{\tilde{d} {\overset{⃑}{ω}}_{2}}{d t} + {\overset{⃑}{ω}}_{2} \times {\overset{⃑}{J}}_{2} \cdot {\overset{⃑}{ω}}_{2} = {\overset{⃑}{M}}_{e}^{2} + {\overset{⃑}{M}}_{n}^{2} .

Corresponding to Eqs. (8-12), there are:

m_{2} \frac{d^{2} x_{o 2}}{d t^{2}} = F_{e}^{2 x} - F_{n}^{x},

m_{2} \frac{d^{2} y_{o 2}}{d t^{2}} = F_{e}^{2 y} - F_{n}^{y},

J_{x_{2}}^{2} {\dot{ω}}_{x_{2}}^{2} + (J_{z_{1}}^{2} - J_{y_{1}}^{2}) ω_{y_{1}}^{2} ω_{z_{1}}^{2} = M_{e}^{2 x_{2}} + M_{n}^{2 x_{2}},

J_{y_{2}}^{2} {\dot{ω}}_{y_{2}}^{2} + (J_{x_{2}}^{2} - J_{z_{2}}^{2}) ω_{z_{2}}^{2} ω_{x_{2}}^{2} = M_{e}^{2 y_{2}} + M_{n}^{2 y_{2}},

J_{z_{2}}^{2} {\dot{ω}}_{z_{2}}^{2} + (J_{y_{2}}^{2} - J_{x_{2}}^{2}) ω_{x_{2}}^{2} ω_{y_{2}}^{2} = M_{e}^{2 z_{2}} + M_{n}^{2 z_{2}} .

Corresponding to Eq. (13), there are:

\{\begin{array}{l} 2 {\dot{λ}}_{0}^{''} = - ω_{x_{2}}^{2} λ_{1}^{''} - ω_{y_{2}}^{2} λ_{2}^{''} - ω_{z_{2}}^{2} λ_{3}^{''}, \\ 2 {\dot{λ}}_{1}^{''} = ω_{x_{2}}^{2} λ_{0}^{''} + ω_{z_{2}}^{2} λ_{2}^{''} - ω_{y_{2}}^{2} λ_{3}^{''}, \\ 2 {\dot{λ}}_{2}^{''} = ω_{y_{2}}^{2} λ_{0}^{''} - ω_{z_{2}}^{2} λ_{1}^{''} + ω_{x_{2}}^{2} λ_{3}^{''}, \\ 2 {\dot{λ}}_{3}^{''} = ω_{z_{2}}^{2} λ_{0}^{''} + ω_{y_{2}}^{2} λ_{1}^{''} - ω_{x_{2}}^{2} λ_{2}^{''} . \end{array}

Corresponding to Eq. (14), there are:

A^{(1,0)} = [\begin{matrix} 2 [{(λ_{0}^{''})}^{2} + {(λ_{1}^{''})}^{2}] - 1 & 2 (λ_{1}^{''} λ_{2}^{''} + λ_{0}^{''} λ_{3}^{''}) & 2 (λ_{1}^{''} λ_{3}^{''} - λ_{0}^{''} λ_{2}^{''}) \\ 2 (λ_{1}^{''} λ_{2}^{''} - λ_{0}^{''} λ_{3}^{''}) & 2 [{(λ_{0}^{''})}^{2} + {(λ_{2}^{''})}^{2}] - 1 & 2 (λ_{2}^{''} λ_{3}^{''} + λ_{0}^{''} λ_{1}^{''}) \\ 2 (λ_{1}^{''} λ_{3}^{''} + λ_{0}^{''} λ_{2}^{''}) & 2 (λ_{2}^{''} λ_{3}^{''} - λ_{0}^{''} λ_{1}^{''}) & 2 [{(λ_{0}^{''})}^{2} + {(λ_{3}^{''})}^{2}] - 1 \end{matrix}] .

3. Analytical calculation of ${\overset{⃑}{F}}_{e}^{1}$ , ${\overset{⃑}{M}}_{e}^{1}$ , ${\overset{⃑}{F}}_{e}^{2}$ and ${\overset{⃑}{M}}_{e}^{2}$

${\overset{⃑}{F}}_{e}^{1}$ is caused by the elastic bending of the face gear shaft 1, and in the case of very small bending deformation, its value can be found by the following relation:

15

F_{e}^{1 x} = - k_{1} x_{o_{1}}, F_{e}^{1 z} = - k_{1} z_{o_{1}} .

where $k_{1}$ is a constant coefficient. If the effect of damping is considered, Eq. (15) can be changed to:

16

F_{e}^{1 x} = - k_{1} x_{o_{1}} - f_{d}^{1} ({\dot{x}}_{o_{1}}), F_{e}^{1 z} = - k_{1} z_{o_{1}} - f_{d}^{1} ({\dot{z}}_{o_{1}}) .

where $f_{d}^{1}$ is the damping coefficient, which is a function of ${\dot{x}}_{o_{1}}$ or ${\dot{z}}_{o_{1}}$ , and the function $f_{d}^{1}$ can be expressed by a polynomial:

17

f_{d}^{1} = d_{1}^{1} \cdot x + d_{2}^{1} \cdot {(x)}^{2} + d_{3}^{1} \cdot {(x)}^{3} + \cdot \cdot \cdot .

where $d_{1}^{1}$ , $d_{2}^{1}$ and $d_{3}^{1}$ are constants.

${\overset{⃑}{M}}_{e}^{1}$ consists of two parts. The first part is the driving torque transmitted from the face gear shaft 1 to the face gear. Its expression in the dynamic coordinate system $o_{1}$ - $x_{1} y_{1} z_{1}$ is:

18

{\overset{⃑}{M}}_{e}^{1} (1) = (\begin{array}{l} 0 & T_{1} & 0 \end{array}) .

The second part is the reaction moment caused by the bending of the face gear shaft 1. When the bending deformation is small, the expression of the second part of ${\overset{⃑}{M}}_{e}^{1}$ is:

19

{\overset{⃑}{M}}_{e}^{1} (2) = c_{1} γ_{1},

where $c_{1}$ is a constant and $γ_{1}$ is the angle representing the amount of bending deformation, which can be obtained by the following formula:

20

c o s γ_{1} = A^{(1,0)} (2,2) .

where $A^{(1,0)}$ represents the direction cosine matrix of the dynamic coordinate system relative to the inertial coordinate system. To find the direction of the moment, write $A^{(1,0)} (2,1)$ and $A^{(1,0)} (2,3)$ in plural form:

21

A^{(1,0)} (2,1) + i A^{(1,0)} (2,3) .

Then multiplying Eq. (21) by the complex number $e^{i \frac{π}{2}} = i$ , we have:

22

- A^{(1,0)} (2,3) + i A^{(1,0)} (2,1) .

Finally, the expression of the second part of ${\overset{⃑}{M}}_{e}^{1}$ in the moving coordinate system $o_{1}$ - $x_{1} y_{1} z_{1}$ is:

23

{\overset{⃑}{M}}_{e}^{1} (2) = \frac{c_{1} γ_{1}}{\sqrt{{(A^{(1,0)} (2,3))}^{2} + {(A^{(1,0)} (2,1))}^{2}}} (\begin{array}{l} - A^{(1,0)} (2,3) & 0 & A^{(1,0)} (2,1) \end{array}) .

When $\sqrt{{(A^{(1,0)} (2,3))}^{2} + {(A^{(1,0)} (2,1))}^{2}} = 0$ , Eq. (23) does not hold, and ${\overset{⃑}{M}}_{e}^{1} (2) = 0$ at this time.

For straight cylindrical gear 2, a similar analysis can be carried out, corresponding to Eqs. (15-17), we have:

F_{e}^{2 x} = - k_{2} x_{o_{2}}, F_{e}^{2 y} = - k_{2} y_{o_{2}},

F_{e}^{2 x} = - k_{2} x_{o_{2}} - f_{d}^{2} ({\dot{x}}_{o_{2}}), F_{e}^{2 y} = - k_{2} y_{o_{2}} - f_{d}^{2} ({\dot{y}}_{o_{2}}),

f_{d}^{2} = d_{1}^{2} \cdot x + d_{2}^{2} \cdot {(x)}^{2} + d_{3}^{2} \cdot {(x)}^{3} + \cdot \cdot \cdot .

Corresponding to Eqs. (18) and (23), we have

{\overset{⃑}{M}}_{e}^{2} (1) = (\begin{array}{l} 0 & 0 & T_{2} \end{array}),

{\overset{⃑}{M}}_{e}^{2} (2) = \frac{c_{2} γ_{2}}{\sqrt{{(A^{(2,0)} (3,2))}^{2} + {(A^{(2,0)} (3,1))}^{2}}} (\begin{array}{l} A^{(2,0)} (3,2) & - A^{(2,0)} (3,1) & 0 \end{array}),

where $T_{2}$ is the load torque of the straight cylindrical gear shaft 2 acting on the straight cylindrical gear. The $A^{(2,0)}$ represents the direction cosine matrix of the dynamic coordinate system 2 relative to the inertial coordinate system.

3.1. Calculation of ${\overset{⃑}{F}}_{n}$ , ${\overset{⃑}{M}}_{n}^{1}$ and ${\overset{⃑}{M}}_{n}^{2}$

${\overset{⃑}{F}}_{n}$ is the meshing force between face gear 1 and straight cylindrical gear 2, and its mathematical model is:

24

|{\overset{⃑}{F}}_{n}| = F_{n} = t a n (k_{F} (t) \cdot f (Δ)) + d_{F} \dot{Δ} .

where $k_{F} (t)$ is the time-varying meshing stiffness; $d_{F}$ is the meshing damping; $Δ$ is the relative displacement along the meshing line; $f (Δ)$ is the clearance function, and its expression is:

25

f (Δ) = \{\begin{array}{l} Δ - b_{0}, & Δ > b_{0}, \\ 0, & |Δ| \leq b_{0}, \\ Δ + b_{0}, & Δ < - b_{0}, \end{array}

where $b_{0}$ is half of the average normal mesh clearance of gear pair.

The expression of the time-varying meshing stiffness $k_{F} (t)$ can be approximated as:

26

k_{F} (t) = {\bar{k}}_{F} + A_{F} s i n (ω_{0} t + φ_{F}),

where ${\bar{k}}_{F}$ is the average meshing stiffness; $A_{F}$ is the vibration amplitude of the meshing stiffness; $ω_{0}$ is the meshing angular frequency; $φ_{F}$ is the initial phase of the engagement stiffness, usually zero.

The expression for the relative displacement $Δ (t)$ along the direction of the engagement line is:

27

Δ (t) = [x_{01} (t) + r_{b 1} θ_{1} (t)] c o s α_{n} + z_{01} (t) s i n α_{n} - [x_{02} (t) + r_{2} θ_{2} (t)] c o s α_{n} - e_{n} (t),

where $r_{b 1}$ is the base circle radius of the straight cylindrical gear; $r_{2}$ is the meshing radius of the face gear; $α_{n}$ is the meshing angle of the gear pair; $e_{n} (t)$ is the comprehensive transmission error of the gear pair, and its expression is:

28

e_{n} (t) = e_{0} + A_{0} s i n (ω_{0} t + φ_{e}),

where $e_{0}$ is the average comprehensive error; $A_{0}$ is the fluctuation amplitude of the comprehensive error; $φ_{e}$ is the initial phase of the comprehensive error; $θ_{1}$ and $θ_{2}$ are the angles of rotation of axis 1 and axis 2 respectively, the expression is:

29

θ_{1} (t) = \int_{0}^{t} ω_{y 1}^{1} (t) d t,

30

θ_{2} (t) = \int_{0}^{t} ω_{z 2}^{2} (t) d t .

The magnitude of the meshing force ${\overset{⃑}{F}}_{n}$ is analyzed above, and the unit vector of its direction is denoted as ${\overset{⃑}{n}}_{a}$ .In the actual meshing transmission process of the face gear, the direction of the meshing point $p$ and the meshing line are complex functions that change with time. To facilitate the analysis of its dynamics, assume that the point of engagement $p$ and the direction of the line of engagement do not change with time. Then the expression of the unit vector ${\overset{⃑}{n}}_{a}$ in the inertial coordinate system is:

31

{\overset{⃑}{n}}_{a} = (\begin{array}{l} - c o s α_{n} & 0 & s i n α_{n} \end{array}) .

The components of vectors $\vec{o_{1} p}$ and $\vec{o_{2} p}$ in the moving coordinate system $o_{1}$ - $x_{1} y_{1} z_{1}$ and $o_{2}$ - $x_{2} y_{2} z_{2}$ are expressed as:

32

\vec{o_{1} p} = (\begin{array}{l} 0 & 0 & - r_{b 1} \end{array}),

33

\vec{o_{2} p} = (\begin{array}{l} 0 & r_{2} & 0 \end{array}) .

According to the definition of torque, the expressions of ${\overset{⃑}{M}}_{N}^{1}$ and ${\overset{⃑}{M}}_{N}^{2}$ are respectively:

34

{\overset{⃑}{M}}_{N}^{1} = \vec{o_{1} p} \times {\overset{⃑}{F}}_{n},

35

{\overset{⃑}{M}}_{N}^{2} = \vec{o_{2} p} \times (- {\overset{⃑}{F}}_{n}) .

4. System dynamics analysis

The above dynamic equations are solved using Euler’s single-step method [23], and the nonlinear dynamic vibration characteristics of the face gear transmission system considering the gyro effect are analyzed. When solving, the parameters of the face gear transmission system are shown in Table 1. The support stiffness and damping in the table are selected from references [24] and [25].

Table 1Parameter table of face gear transmission system

Symbol	Quantity	Numerical value
$z_{2}$	Number of face gear teeth	120
$z_{1}$	Number of cylindrical gear teeth	40
$m$	Gear module	3 mm
$α_{n}$	Pressure angle	25°
$h$	Tooth width	25 mm
$p$	Input power	10 Kw
$m_{1}$	Quality of straight cylindrical gear	2.65 kg
$m_{2}$	Quality of face gear	7.72 kg
$k_{2}$	Face gear support stiffness	5×10⁹N/m
$k_{1}$	Straight cylindrical gear support stiffness	4×10⁹N/m
$c_{2}$	Face gear support damping	4×10⁵N·s·m^-1
$c_{1}$	Straight cylindrical gear support damping	3×10⁵N·s·m^-1
$k_{m}$	Average meshing stiffness	3×10⁸N/m
$c_{s}$	Engagement damping	1×10⁵N·s·m^-1
$n$	Input speed	3000 r/min

Fig. 4Vibration displacement along x-axis direction

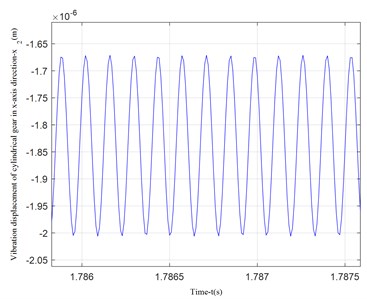
a) Vibration displacement in $x$ -axis direction of cylindrical gear

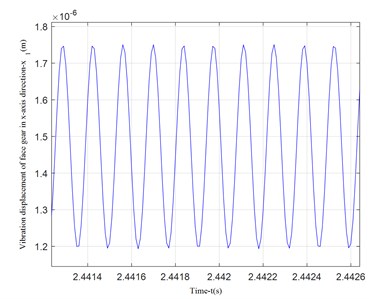
b) Vibration displacement in $x$ -axis direction of face gear

It can be seen from Fig. 4 that the vibration displacement of the face gear is about 1/3 larger than the vibration displacement of the straight cylindrical gear. Because the cylindrical gear in the model has a smaller bending moment and smaller deformation, the calculation results are in line with engineering reality. Comparing the vibration displacement in the $x$ -axis and $z$ -axis directions of the face gear in Figs. 4 and 5, the vibration displacement in the $z$ -axis direction of the face gear is smaller than the vibration displacement in the $x$ -axis direction, this is because the component force of the meshing force in the x-axis direction is small, and the calculation result is consistent with the force analysis result.

According to the analysis in Fig. 6, it can be seen that the vibration speed period of the $x$ -axis and $z$ -axis of the face gear is the same. However, the vibration velocity in the $x$ -axis direction is greater than that in the $z$ -axis direction, which is consistent with the vibration displacement analysis results of Figs. 4 and 5.Fig. 7 shows the vibration velocity of the cylindrical gear in the $x$ -axis and $y$ -axis directions, the vibration velocity in the $x$ -axis direction of the cylindrical gear and the vibration velocity in the $x$ -axis direction of the face gear in Fig. 6 are both periodic vibrations, the vibration speed in the $y$ -axis direction is a straight line. This is due to the transmission characteristics of the face gear. The face gear and the cylindrical gear are not stressed in the y-axis direction, so no vibration will occur.

Fig. 5Vibration displacement in the z-axis direction of the face gear

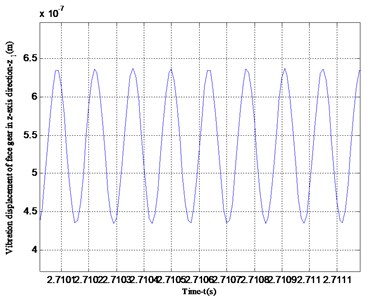
Fig. 6Vibration speed of face gear in x-axis and z-axis directions

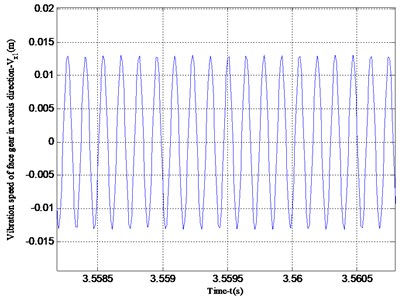
a) Vibration speed in $x$ -axis direction of face gear

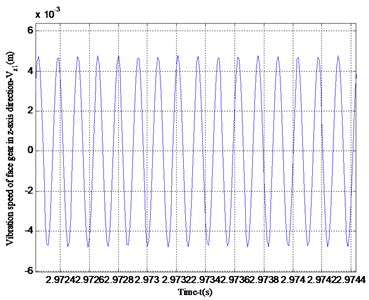
b) Vibration speed in $z$ -axis direction of face gear

Fig. 7Vibration speed in the x-axis and y-axis directions of the cylindrical gear

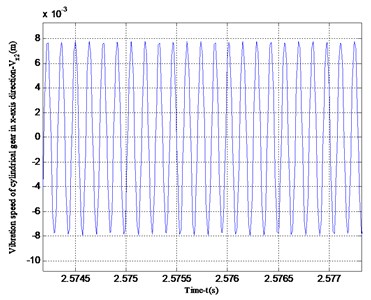
a) Vibration speed in $x$ -axis direction of cylindrical gear

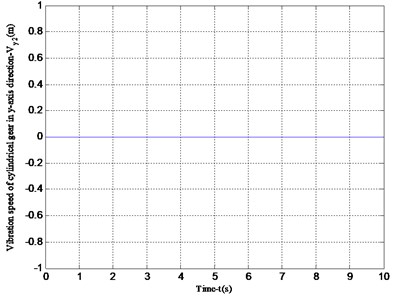
b) Vibration speed in $y$ -axis direction of cylindrical gear

Fig. 8 shows the vibration acceleration of the straight cylindrical gear in the $x$ -axis and $y$ -axis directions. Since the straight cylindrical gear does not vibrate in the $y$ -axis direction, its vibration acceleration is 0, and the period of the vibration velocity is the same as that in Fig. 7. Figs. 9 and 10 are the angular velocity and angular acceleration of the torsional vibration of the center of mass of the face gear and the straight cylindrical gear around the $y$ -axis. Since the gear ratio of the face gear and the straight cylindrical gear is 3, the calculation result has a period ratio of 3, which is consistent with the actual result.

Fig. 8Vibration acceleration in the x-axis and y-axis directions of the cylindrical gear

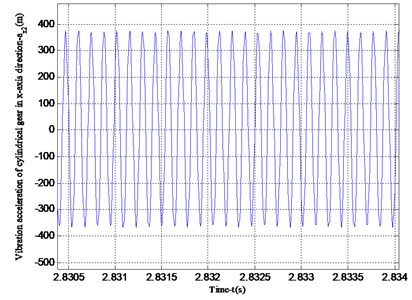
a) Vibration acceleration in $x$ -axis direction of cylindrical gear

b) Vibration acceleration in $y$ -axis direction of cylindrical gear

Fig. 9Angular velocity and angular acceleration of face gear vibrating around the y-axis

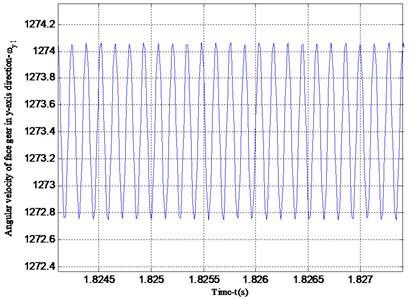
a) Angular velocity of face gear vibration around $y$ -axis

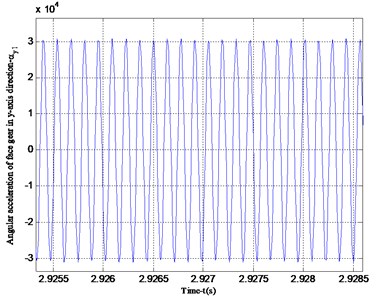
b) Angular acceleration of face gear vibration around $y$ -axis

Fig. 10Angular velocity and angular acceleration of cylindrical gear vibrating around the y-axis

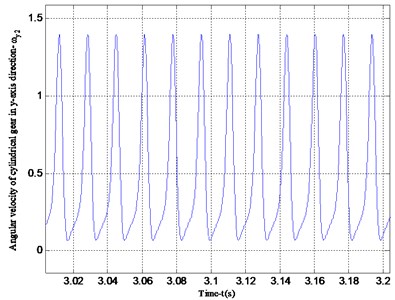
a) Angular velocity of cylindrical gear vibrating around $y$ -axis

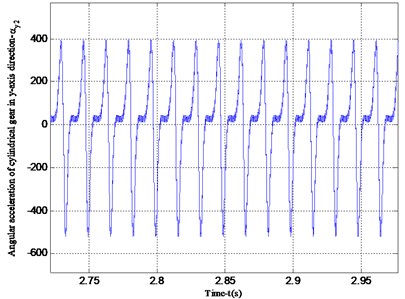
b) Angular acceleration of cylindrical gear vibration around $y$ -axis

Fig. 11Plane phase diagram of the vibration of the face gear transmission system

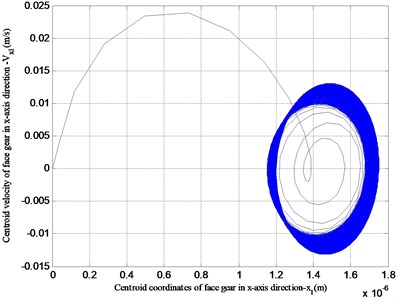
a) Face gear drive plane phase diagram

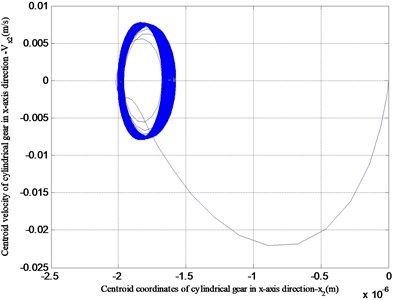
b) Cylindrical gear drive plane phase diagram

Fig. 11 is a plane phase diagram of the x-coordinate of the center of mass of the face gear transmission system. The $x$ -coordinates of the straight cylindrical gear and the face gear have a large change when starting, but tend to be stable after stable operation, which is consistent with engineering practice.

According to the above vibration characteristics of the face gear obtained by numerical analysis considering the gyroscopic effect, compared with the results of the vibration characteristics of the face gear without considering the gyroscopic effect in the literature [25-27], it can be seen that the vibration displacement, vibration velocity, and vibration angular velocity are relatively small in the face gear drive with high speed. According to the plane phase diagram of the center of mass, it can be seen that the face gear and the cylindrical gear gradually stabilize within a relatively small vibration displacement. Therefore, it is necessary to consider gyroscopic effects in high speed face gear drives.

5. Conclusions

Establish a dynamic model of the orthogonal face gear transmission system. The gyro effect of the gear around its center of mass during the face gear transmission is considered in the model. It also includes time-varying meshing stiffness, tooth surface error, support stiffness, support damping and other factors, which can more comprehensively describe the vibration characteristics of face gear transmission.

Adopt Euler parameter method to establish the nonlinear dynamic equation of the face gear transmission system considering the gyro effect and solve it to obtain the dynamic response characteristics of the face gear transmission system.

The vibration characteristics of the face gear transmission system are more complicated, and it is very important for the high-speed and heavy-duty helicopter transmission system. Therefore, it is particularly important to establish a dynamic model that can better reflect the real working conditions, and it has important theoretical guiding significance for improving the stability, service life and the vibration and noise reduction of the system.

References

Handschud R. F., Lewicki D. G., and Bossler R. B., “Experimental Testing of Prototype Face Gears for Helicopter Transmissions,” NASA-TM-105434, 1992.

Search CrossRef
F. L. Litvin, J.-C. Wang, R. B. J. Bossler, Y.-J. D. Chen, G. Heath, and D. G. Lewicki, “Application of face-gear drives in helicopter transmissions,” in International Power Transmission and Gearing Conference, Sep. 2013.

Search CrossRef
F. L. Litvin, J.-C. Wang, R. B. Bossler, Y.-J. D. Chen, G. Heath, and D. G. Lewicki, “Application of face-gear drives in helicopter transmissions,” Journal of Mechanical Design, Vol. 116, No. 3, pp. 672–676, Sep. 1994, https://doi.org/10.1115/1.2919434

Publisher
F. L. Litvin, C.-L. Hsiao, J.-C. Wang, and X. Zhou, “Computerized simulation of generation of internal involute gears and their assembly,” Journal of Mechanical Design, Vol. 116, No. 3, pp. 683–689, Sep. 1994, https://doi.org/10.1115/1.2919436

Publisher
F. L. Litvin, A. Egelja, J. Tan, and G. Heath, “Computerized design, generation and simulation of meshing of orthogonal offset face-gear drive with a spur involute pinion with localized bearing contact,” Mechanism and Machine Theory, Vol. 33, No. 1-2, pp. 87–102, Jan. 1998, https://doi.org/10.1016/s0094-114x(97)00022-0

Publisher
D. G. Lewicki, R. F. Handschuh, G. F. Heath, and V. Sheth, “Evaluation of Carburized and Ground Face Gears,” NASA-TM-1999-209188, Sep. 2013.

Search CrossRef
Y. Chen and R. Bossler, “Design, analysis, and testing methods for a split-torque face-gear transmission,” in 31st Joint Propulsion Conference and Exhibit, Jul. 1995, https://doi.org/10.2514/6.1995-3051

Publisher
Chung T. D. and Chang S. H., “The undercutting and pointing of face gear,” Journal of the Chinese Institute of Engineering, Vol. 21, No. 2, 1998.

Publisher
Andrei G., “Advanced face gear technology for rotorcraft drive trains,” in Proceedings of the 24th European Rotorcraft Forum, 1998.

Search CrossRef
Chang S. H. and Chung S. D., “Analysis of the kinematic error of a face gear harmonic drive,” Chinese Society of Mechanical Engineering, Vol. 19, No. 4, 1998.

Search CrossRef
Litvin F. L., “Apparatus and method for precision grinding face gear,” America US006146253-A-[P], 2000.

Search CrossRef
F. L. Litvin, A. Egelja, J. Tan, D. Y.-D. Chen, and G. Heath, “Handbook on Face Gear Drives with a Spur Involute Pinion,” NASA CR-209909, Sep. 2013.

Search CrossRef
Frąckowiak, P., Ptaszyński, W., Stoić, and A., “New geometry and technology forming face-gear with circle line of teeth on CNC milling machine,” Metalurgija, Vol. 51, No. 1, pp. 109–112, 2012.

Search CrossRef
X.-Z. Deng, G.-G. Li, B.-Y. Wei, and J. Deng, “Face-milling spiral bevel gear tooth surfaces by application of 5-axis CNC machine tool,” The International Journal of Advanced Manufacturing Technology, Vol. 71, No. 5-8, pp. 1049–1057, Mar. 2014, https://doi.org/10.1007/s00170-013-5499-3

Publisher
Z. C. Chen and M. Wasif, “A generic and theoretical approach to programming and post-processing for hypoid gear machining on multi-axis CNC face-milling machines,” The International Journal of Advanced Manufacturing Technology, Vol. 81, No. 1-4, pp. 135–148, Oct. 2015, https://doi.org/10.1007/s00170-015-7171-6

Publisher
D. Liu, T. Ren, and X. Jin, “Geometrical model and tooth analysis of undulating face gear,” Mechanism and Machine Theory, Vol. 86, pp. 140–155, Apr. 2015, https://doi.org/10.1016/j.mechmachtheory.2014.12.004

Publisher
Y. Wang, Z. Lan, L. Hou, H. Zhao, and Y. Zhong, “A precision generating grinding method for face gear using CBN wheel,” The International Journal of Advanced Manufacturing Technology, Vol. 79, No. 9-12, pp. 1839–1848, Aug. 2015, https://doi.org/10.1007/s00170-015-6962-0

Publisher
X.-L. Peng, L. Zhang, and Z.-D. Fang, “Manufacturing process for a face gear drive with local bearing contact and controllable unloaded meshing performance based on ease-off surface modification,” Journal of Mechanical Design, Vol. 138, No. 4, Apr. 2016, https://doi.org/10.1115/1.4032579

Publisher
K. Kawasaki, H. Gunbara, and H. Tamur, “Study of meshing of gear teeth,” in Proc. of JSME International Conference on Motion and Power Transmissions, pp. 82–86, 2009.

Publisher
I. Tsuji, H. Gunbara, K. Kawasaki, and A. Takami, “Machining and running test of high-performance face gear set,” in ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Jan. 2011, https://doi.org/10.1115/detc2011-48824

Publisher
Sui Yongfeng and Lv Hexiang, “Influence of gyroscopic term to the vibration of rotor system,” (in Chinese), Chinese Journal of Computational Mechanics, Vol. 6, pp. 711–714, 2003.

Search CrossRef
Liu Weijia, “Impact of gyroscopic effect on the critical speed of the rotor,” (in Chinese), Journal of Jilin Normal University, Vol. 33, No. 3, pp. 47–49, 2012.

Search CrossRef
Wen Bangchun, Theory of Mechanical Vibration and Its Applications. (in Chinese), Beijing: Higher Education Press, 2009.

Search CrossRef
Li Xiaozhen, Zhu Rupeng, Li Zhengminqing, and Jin Guanghu, “Influences of frictional coefficient on vibration characteristic of face-gear transmission system,” (in Chinese), Zhendong Gongcheng Xuebao, Vol. 27, No. 4, pp. 583–588, 2014.

Search CrossRef
Yang Zhen, Wang Sanmin, Fan Yeseng, and Liu Haixia, “Nonlinear dynamics of face-gear transmission system,” (in Chinese), Journal of Vibration and Shock, Vol. 29, No. 9, pp. 218–221, 2010.

Search CrossRef
Lin Tengjiao and Ran Xiongtao, “Nonlinear vibration characteristic analysis of a face-gear drive,” (in Chinese), Zhendong yu Chongji, Vol. 31, No. 2, pp. 25–31, 2012.

Search CrossRef
Jin Guanghu, Zhu Rupeng, and Bao Heyun, “Nonlinear dynamical characteristics of face gear transmission system,” (in Chinese), Journal of Central South University (Science and Technology), Vol. 41, No. 5, pp. 1807–1813, 2010.

Search CrossRef

About this article

Received

09 November 2021

Accepted

02 February 2022

Published

30 June 2022

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/jve.2022.22289

Keywords

dynamic response

gyroscopic effect

orthogonal face gears

Acknowledgements

This work is supported by the Spent Fuel Dissolver Project of the Ministry of Nuclear Industry of the People’s Republic of China.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 12 30

Modelling and dynamic behaviours of a high-contact-ratio spur-gear system considering rough surface

Zhenbang Cheng, Yu Zhou, Zhengyu Liu

Research article

2016 12 08

Constructed solutions of face gear dynamics associated with engagement impact energy decay

Zhengminqing Li, Hao Wu, Rupeng Zhu

Research article

2016 02 15

Effect predictions of star pinion geometry phase adjustments on dynamic load sharing behaviors of differential face gear trains

Zhengminqing Li, Wei Ye, Linlin Zhang, Rupeng Zhu

Research article

2015 12 30

Nonlinear dynamic analysis for high speed gear-rotor-bearing system of the large scale wind turbine

Shihua Zhou, Guiqiu Song, Mengnan Sun, Zhaohui Ren

X. Li, K. Su, T. Li, and L. Zhang, “Vibration characteristics analysis of face gear transmission system considering gyroscopic effect,” Journal of Vibroengineering, Vol. 24, No. 4, pp. 624–636, Jun. 2022, https://doi.org/10.21595/jve.2022.22289

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2022.22289
UR  - https://doi.org/10.21595/jve.2022.22289
TI  - Vibration characteristics analysis of face gear transmission system considering gyroscopic effect
T2  - Journal of Vibroengineering
AU  - Li, Xiaozhen
AU  - Su, Kuo
AU  - Li, Tongjie
AU  - Zhang, Liyong
PY  - 2022
DA  - 2022/06/30
PB  - JVE International Ltd.
SP  - 624-636
VL  - 24
IS  - 4
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Li_2022,
	doi = {10.21595/jve.2022.22289},
	url = {https://doi.org/10.21595/jve.2022.22289},
	year = 2022,
	month = {mar},
	publisher = {{JVE} International Ltd.},
	volume = {24},
	number = {4},
	pages = {624--636},
	author = {Xiaozhen Li and Kuo Su and Tongjie Li and Liyong Zhang},
	title = {Vibration characteristics analysis of face gear transmission system considering gyroscopic effect},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]X. Li, K. Su, T. Li, and L. Zhang, “Vibration characteristics analysis of face gear transmission system considering gyroscopic effect,” Journal of Vibroengineering, vol. 24, no. 4, pp. 624–636, Mar. 2022, doi: 10.21595/jve.2022.22289.

Copy IEEE

Copied to clipboard!

Li, Xiaozhen, Kuo Su, Tongjie Li, and Liyong Zhang. “Vibration Characteristics Analysis of Face Gear Transmission System Considering Gyroscopic Effect.” Journal of Vibroengineering 24, no. 4 (March 4, 2022): 624–36. https://doi.org/10.21595/jve.2022.22289.

Copy Chicago

Copied to clipboard!

Vibration characteristics analysis of face gear transmission system considering gyroscopic effect

Abstract

Highlights

1. Introduction

2. System dynamics modeling

3. Analytical calculation of F⃑e1, M⃑e1, F⃑e2 and M⃑e2

3.1. Calculation of F⃑n, M⃑n1 and M⃑n2

4. System dynamics analysis

5. Conclusions

References

About this article

Related Articles

3. Analytical calculation of ${\overset{⃑}{F}}_{e}^{1}$ , ${\overset{⃑}{M}}_{e}^{1}$ , ${\overset{⃑}{F}}_{e}^{2}$ and ${\overset{⃑}{M}}_{e}^{2}$

3.1. Calculation of ${\overset{⃑}{F}}_{n}$ , ${\overset{⃑}{M}}_{n}^{1}$ and ${\overset{⃑}{M}}_{n}^{2}$