Multi source heterogeneous data diagnosis method of rotating machinery based on parameter collaborative optimization of multi-scale convolutional autoencoder

1. Introduction

With the popularization of digital transformation in manufacturing enterprises, enterprises usually deploy multiple sensors in the industrial production process to monitor the status of equipment, and collect a large amount of multi-source heterogeneous data, such as vibration signals collected by vibration sensors and current signals collected by current sensors and other time-series data. These data exhibit characteristics such as large volume, heterogeneous sources, and low value density. Although their sources and manifestations are different, they are all descriptions of the status of the same device. Different data sources complement each other, which can avoid the state evaluation bias caused by one single sensor signal and reflect the condition of the device comprehensively from different perspectives [1].

In recent years, with the rapid development of deep learning in the fault diagnosis field [2-6], the achievements in fault diagnosis based on multi-source heterogeneous data and deep learning also have been particularly outstanding. Reference [7] proposed a bearing fault diagnosis method that combines multi-source data fusion with improved attention mechanism. By introducing attention mechanism, the information weights of different data sources can be adjusted dynamically, with good robustness and adaptability. Reference [8] proposed a selective convolutional deep residual network based on channel space attention mechanism and feature fusion. This network utilizes channel space attention mechanism to assign different weights to different channels, and integrates the features of different channels and different levels of feature information, which improves the efficiency of fault recognition. Reference [9] proposed a hybrid deep neural network designed specifically for estimating remaining useful life. This network utilizes LSTM to extract temporal features from multi-sensor data and CNN to extract spatial features, demonstrating better generalization ability in complex prediction scenarios with increasing operating conditions and fault modes. Reference [10] utilized generative adversarial networks to extract features from multi-sensor data, and finally used variational autoencoders to achieve bearing state evaluation and remaining service life prediction, providing a new solution for equipment health management based on multi-sensor data. Reference [11] concatenated multi-sensor signals and inputted them into a multi-channel fusion feature extractor, and combined them with a bidirectional long short-term memory (BiLSTM) network to construct a bearing health index. Reference [12] proposed a convolutional autoencoder with improved loss function, which can capture the degradation process of bearings effectively, extract the health status features of bearings from multi-sensor data, and avoid the loss of local information. Reference [13] merged each sensor data by channel to achieve efficient fusion of multi-sensor data. Reference [14] proposed a multimodal convolutional neural network that can learn fault related sensitive features from vibration signals and infrared images automatically, and fuse these deep features using T-SNE (T-Distributed Stochastic Neighbor Embedding, T-SNE). Reference [15] used one-dimensional CNN to extract features from vibration signals and sound signals respectively, and fused these features. Compared with the algorithm based on single mode sensor, this method had higher diagnostic accuracy. Literature [16] proposed an improved multi head attention mechanism to extract the features of different sensor signals, and designed a bilinear model to achieve fine fusion of features, which can extract complementary fault information between different signals effectively. Reference [17] proposed a deep coupled autoencoder model for learning joint features of vibration and acoustic signals. Reference [18] alternately extracted and fused one-dimensional temporal data features and two-dimensional image data features based on stacked autoencoders, fully utilizing the correlation and complementarity of multi-source heterogeneous data. Reference [19] proposed an integrated network based on multiple CNN and BiLSTM with compression excitation mechanism in parallel. Reference [20] proposed a convolutional long short-term memory (CLSTM) network, which used CNN to capture shallow features of individual sensors, and then captures deep features through CLSTM. Reference [21] proposed a novel multi-sensor selection framework. The framework can determine adaptively which sensors were used to predict the remaining service life, and explained how different sensors affect the final result of the remaining service life prediction over time. Reference [22] proposed an end-to-end multi-sensor data fusion method based on LSTM encoder decoder structure. Reference [23] used multiple different deep belief networks (DBNs) to extract data features with different sources and structures, and proposed a weight matrix to fuse the decision results of different DBNs. Reference [24] proposed a multi-sensor data fusion method for device health indicators.

Although the above stated deep learning diagnostic models based on multi-source heterogeneous data have achieved high diagnostic accuracy, most of them have not been evaluated based on comprehensive factors such as multi-source heterogeneous feature extraction effectiveness and model diagnostic efficiency to assess the effectiveness of constructed model. Based on this, this paper proposes a multi-source heterogeneous data diagnosis method based on parameter collaborative optimization of MSCAE. Compared to most the current idea of building models based on one single factor, the hybrid model is constructed based on comprehensive factors such as multi-source heterogeneous feature extraction effectiveness, model diagnostic efficiency, and noise resistance, which is more comprehensive and applicable. The main contributions of the paper are as follows:

1) A multi-scale information learning module considering different spatial scales is integrated into CAE to construct a new model named as MSCAE, enhancing its ability to extract features from heterogeneous multi-source information while considering feature information at different spatial scales to improve its noise suppression capability.

2) The sparse attention mechanism is introduced into the MSCAE model to further improve the recognition rate of the model for key fault features.

3) To improve the training and diagnostic efficiency of MSCAE, a quantum particle swarm optimization module is used to perform hyperparameter optimization on the MSCAE model using chaos initialization and dynamic weight strategy.

The remains of the paper are arranged as following: Section 2 is dedicated to the related theories. Section 3 presents the proposed integrated model and diagnostic process. Experiment verification and conclusion are presented in Section 4 and Section 5 respectively.

2. Related theories

2.1. Multi-scale convolutional autoencoder

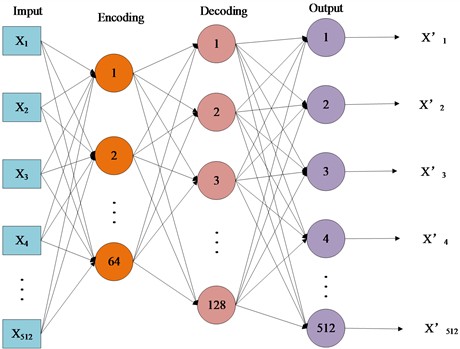
The basic structure of CAE consists of an encoder and a decoder, as shown in Fig. 1. The encoder gradually reduces the spatial dimension of data through convolutional and pooling layers, while increasing the number of feature channels to extract more abstract feature representations. On the other hand, the decoder gradually restores the spatial dimension of the data through the deconvolution layer (or transposed convolution layer), while reducing the number of feature channels needed to reconstruct the original data.

Fig. 1The basic structure of CAE

The encoder part can be represented as follows:

1

$h=f\left(X\right)=f_{encoder}\left(X\right),$

where $h$ represents the decoded feature. The encoder part can be implemented using convolution and pooling operations, which can be expressed as follows:

2

$h=\sigma \left(Conv\left(X,W\right)+b\right),$

where $Conv\left(X,W\right)$ performs convolution operation on the input data $X$. $W$ is the convolution kernel, $b$ represents the bias term, and $\sigma$ is the activation function (which can be sigmoid or ReLU function).

The decoder part can be represented as follows:

3

$X^{\text{'}}= g\left(h\right)=g_{decoder}\left(h\right),$

where $X\text{'}$ represents the reconstructed data. Convolution and upsampling operations can be used to implement the decoder part, as follows:

4

$X^{\text{'}}=\sigma \left(Conv\left(Upsample\left(h\right),W^{\text{'}}\right)+b^{\text{'}}\right).$

In the formula, $Upsample\left(h\right)$ represents the upsampling operation on the decoded features, $W^{\text{'}}$ is the convolution kernel of the decoder, $b^{\text{'}}$ is the bias term of the decoder, and $\sigma$ is the activation function.

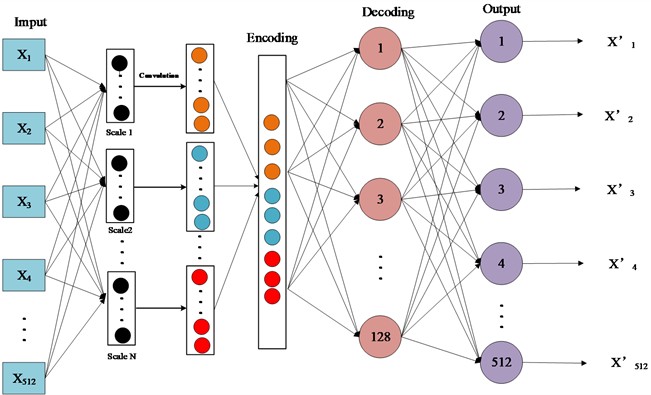
The encoding in traditional CAE mainly uses fixed scale convolutional kernels for feature extraction. The kernel scale of each convolutional layer remains unchanged, limiting the ability to extract classification information at different resolutions and kernel scales. Especially in the case of variable operating condition, extracting deeper level features for diagnosis becomes more challenging. The structure of MS-CAE is adding a layer of kernels with different scale before the encoding layer of original CAE, as shown in Fig. 2, and corresponding multi scale information learning could be realized. Multi scale information learning can capture information more comprehensively and diversely by introducing convolution operators or pooling operations of different scales, further enhancing the model’s understanding of data. Therefore, integrating multi-scale information learning modules into the encoding of CAE can help constructing new MSCAE models and discover more elastic key features. This module combines kernels of different scales and considers feature information at different spatial scales, thereby improving the ability to suppress noise and redundant feature information, and enhancing the model’s representation and classification performance of data. The MSCAE model encodes information during the network training phase, and the defined loss function is as following:

5

$Loss=H\left(p\left(x\right),q\left(x\right)\right)=-{\sum }_{x}p\left(x\right)\log q\left(x\right),$

where $Loss$ refers to the loss function, $p\left(x\right)$ is the target distribution, and $q\left(x\right)$ is the estimated distribution.

The gradient of the backpropagation output layer for MSCAE can be described roughly as following:

6

${\delta }^L=\frac{\partial L(w,b)}{\partial z^L}=\frac{\partial L(w,b)}{\partial x^L}\otimes {\sigma }^{\text{'}}\left(z^L\right),$

where $\delta$ is the gradient, $\otimes$ represents the operation of the matrix, and $\partial$ represents solving for the partial derivative. The function of Eq. (6) is to avoid gradient explosion of MSCAE.

Fig. 2The basic structure of MS-CAE

3. The proposed integrated model and diagnostic process

On the basis of the proposed MSCAE, this article combines it with sparse attention mechanism to propose an ensemble model. This ensemble model combines convolution kernels of different scales to consider feature information at different spatial scales, while embedding a sparse attention mechanism specifically designed for processing multi-source signal data to capture its core features, thereby effectively improving the noise suppression and redundant feature information removal capabilities of the ensemble model.

The integrated model implants sparse attention mechanism between the convolutional layers of the autoencoder layers of MSCAE, with the specific formula as following:

where ⊙ represents element multiplication operation to create attention guided feature maps before pooling.

The clustering centers and features generated by MSCAE are optimized using the following loss function:

where ${\mu }_i$ is a learnable parameter that is updated through backpropagation.

During the training phase, the synchronization process is as follows:

Reconstruct the decoder using cluster conditional deconvolution:

Choosing an appropriate parameter optimization strategy is an important step in improving the efficiency of hybrid model training and diagnosis. To reduce the experimental time for parameter optimization of this model, the proposed QPSO-DWY algorithm is applied to the parameter optimization of the integrated model.

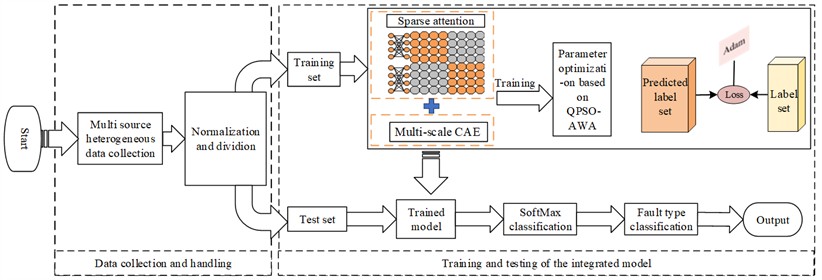
The diagnostic process based on the proposed integrated model and parameter optimization strategy is shown in Fig. 3, as follows:

1) Data preparation: Normalize the collected multi-source heterogeneous data and divide it into training and testing sets.

2) Feature extraction: Output the training set to the ensemble model for model training, and synchronously optimize the model hyperparameters based on the QPSO-DYS algorithm to complete the training of the ensemble model.

3) Classification and diagnosis: Input the test set into the trained ensemble model for fault classification.

4) Evaluation and visualization: using t-SNE for dimensionality reduction, model performance evaluation, and parameter optimization.

Fig. 3Diagnosis flow chart based on the proposed hybrid model

4. Experiment

The method was validated using the NSK 6205 DDU bearing dataset from the Korea Mechanical Research Institute [26]. The experimental testing system consists of a three-phase induction motor, torque sensor, gearbox, two bearing seats, one rotor, and one hysteresis brake, as shown in Fig. 4. The bearing seats are designed in an easy disassembly mode to facilitate the installation of bearings of different running states, and the corresponding heterogeneous data of each running states are collected separately. Five operating states of rolling bearings including healthy bearing, Inner race fault (0.3 mm), Inner race fault (1.0 mm), Outer race fault (0.3 mm), Inner race fault (0.3 mm) are conducted, and the five states are represented by 0, 1, 2, 3 and 4 respectively. Fig. 5 shows the points of failure from the faulty bearings.

The test runs at speed of 3010 RPM, with torque applied to braking and load of 0, 2, and 4 Nm, respectively. Acoustic data is collected without load. Variable load test simulates bearing damage occurring on inner or outer race. The heterogeneous data of five types of running states include vibration, acoustic, and current data of healthy bearings under 0 Nm load, temperature data under 2 Nm load, inner and outer race fault data of 0.3 mm and 1.0 mm under 0 Nm load, and temperature data under 2 Nm load. The time-domain waveforms of the collected signals are shown in Fig. 6.

Fig. 4The test rig

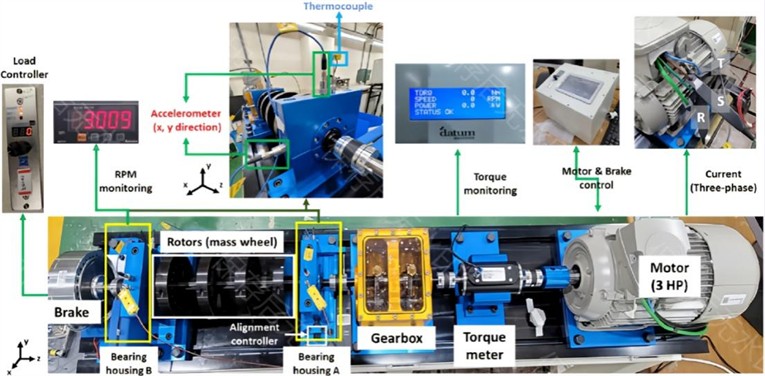
Fig. 5Bearing by crack size: a) inner race 0.3 mm, b) inner race 1.0 mm, c) inner race 3.0 mm, d) outer race 0.3 mm, e) outer race 1.0 mm, f) outer race 3.0 mm

a)

b)

c)

d)

e)

f)

Fig. 6Time-domain waveforms of five kinds of heterogeneous data

a) Vibration data

b) Temperature data

c) Acoustic data

d) Current data

In this study, standardization and sliding window methods are used to preprocess the network input data. Due to the large amount of single fault data, a window length of 4096 data points and a step size of 64 are used to create training data, which is randomly divided into datasets for training and testing. The details of multi-source sample division are shown in Table 1. Among them, the sliding window method is mainly used to extract multiple overlapping samples from the input sequence (as shown in Fig. 7). Then 38×4 sets of heterogeneous sample sets are chosen for each state, that is to say that there are all 760×4 sets of heterogeneous sample sets obtained for the five running states in the four loading states. Select 2900 sets of sample sets from 760×4 sets randomly and divide them into training set sand testing sets in 7:3 ratio, and the corresponding number of training sets and test sets 2030 (406×5) and 870 (174×5) respectively.

Fig. 8 shows the diagnostic results. The confusion matrix and t-SNE classification showed good results without misclassification. Based on Fig. 8(a) and 8(b), the following phenomenon could be observed: the optimization step size is dynamically adjusted through the cyclic learning rate (CLR) strategy. The model converges rapidly in the early stage of training and avoids overfitting in the later stage, and the verification loss tends to be stable. Based on Fig. 8(c) and 8(d): the confusion matrix shows that the classification accuracy rate of the model for all categories reaches 100 %, and the clear clustering effect of feature embedding further verifies the feature extraction ability of the model. The self-attention mechanism improves the feature fusion effect significantly, the QPSO-DYS optimization accelerates the convergence speed, and the dynamic learning rate strategy reduces the risk of overfitting effectively.

Fig. 7Sliding window data augmentation

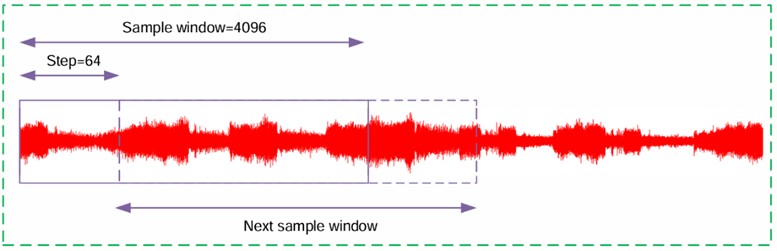
Fig. 8Diagnosis results

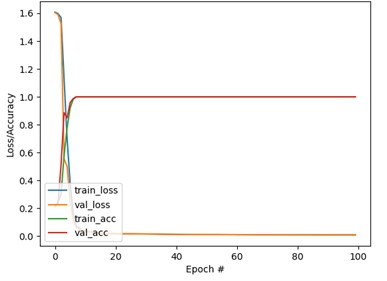
a) The curves of precision and loss rate

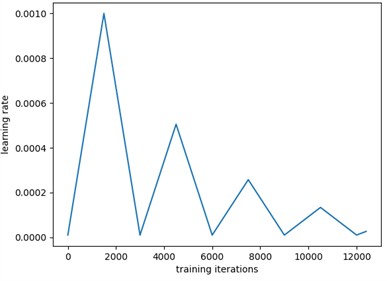
b) The variable learning rate curve

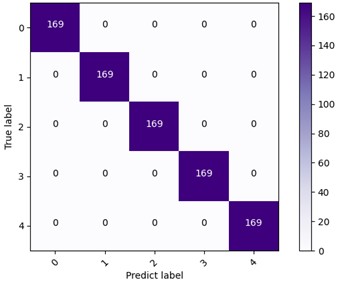
c) The confusion matrix diagram

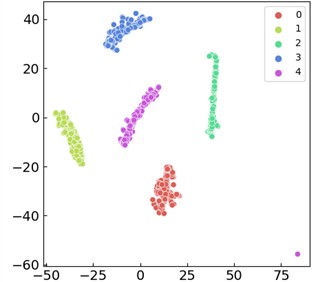
d) The visualization diagram of t-SNE

To verify the advantages of the proposed method, the following models are used for comparison: WDCNN, ResNet, WDCNN-VLR-AE, WDCNN-VLR-SE, WDCNN-SE-AE (the hyperparameter settings and other details of these comparison methods are set in the same way as in their respective literature). Fig. 9 shows the average diagnostic accuracy of each model after multiple experiments. The model presented in this article exhibits the highest accuracy of 98.5 % and the lowest loss rate of 1.7 %. Specifically, the accuracy of our model is significantly higher than other compared models, indicating that it has stronger discriminative ability and higher accuracy in fault classification tasks. Meanwhile, the loss rate of our model is significantly lower than other models, indicating that it can converge more effectively during training and has better stability.

ResNet and WDCNN perform relatively poorly. Their accuracy is 25.7 % and 27.6 % lower than this model, indicating poor feature extraction ability and difficulty in fully utilizing key information buried in the data. In addition, the loss rates of ResNet and WDCNN are 11.1 % and 12.6 % higher than the model in this paper, which may be related to their model structure and optimization algorithm, leading them to easily fall into local optima, thereby affecting overall performance.

In contrast, WDCNN-VLR-AE, WDCNN-VLR-SE, and WDCNN-SE-AE showed a 10.5 %, 14.6 %, and 7.5 % decrease in accuracy compared to our model on the NSK 6205 DDU dataset, while the loss rate increased by 5 %, 8.2 %, and 4.1 %, respectively, demonstrating an improvement in feature extraction, classification, and outlier resolution capabilities for the dataset.

Fig. 9Comparison results

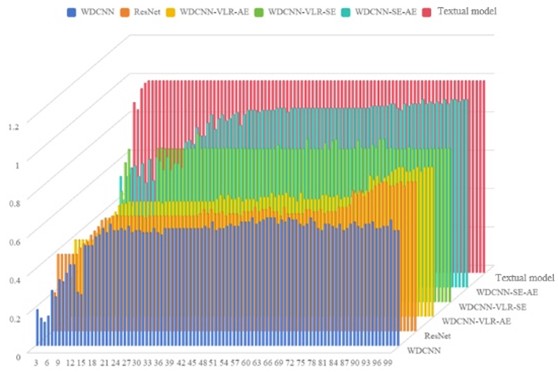
a) The accuracy rate of kinds of models after multiple experiments

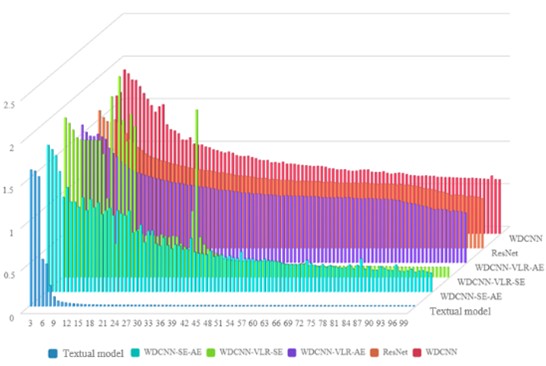
b) The loss rate of kinds of models after multiple experiments

The radar chart shown in Fig. 10 further demonstrates the accuracy and loss rate of the dataset based on the proposed model after ten times of experiments. The comparison results show that the model proposed in this paper exhibits excellent performance under the same operating conditions. Specifically, the model presented in this article was able to maintain the lowest loss rate and highest accuracy in ten experiments, with significantly higher accuracy than other models and significantly lower loss rate than others. This indicates that it has better stability and convergence when dealing with multi-source heterogeneous data.

Fig. 10Radar chart results

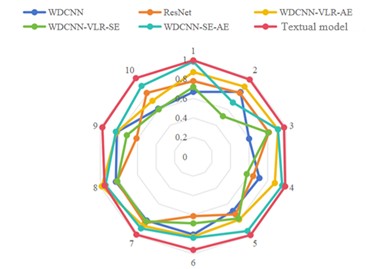
a) Precision rate chart

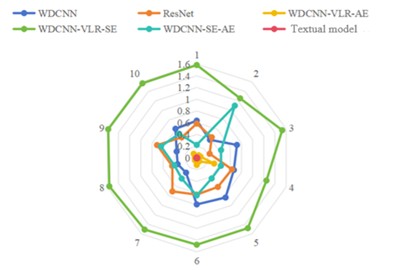
b) Loss rate chart

In terms of model diagnosis and performance evaluation, we have recorded the following key indicators to comprehensively reflect the efficiency and performance of the model. The computer configuration used in the experiment is: Intel Core AMD RyzenTM9-5900HX processor, with a clock speed of 3.3 GHz, equipped with NVIDIA GeForce RTX 3080 graphics card (16 GB of video memory), the system is equipped with 32GB of memory, runs Windows 11 Home Edition, and is equipped with solid-state memory, with a total capacity of about 2TB. In order to demonstrate the advantages of the method compared to the comparative method from multiple perspectives, Table 2 presents score statistics from multiple dimensions such as time efficiency and F1 score.

In order to compare the advantages of optimizing parameters in this article, several parameter optimization models were compared, as shown in Table 3. From the table, it can be seen that the parameter optimization model in this article saves a lot of training time relatively, and the final training accuracy and loss rate are only reduced by 0.1 % and 0.2 %, and the loss rate is only increased by 0.2 % and 0.2 % compared to manual parameter tuning one by one.

5. Conclusions

This paper proposes a hybrid diagnostic model that integrates MSCAE and sparse attention mechanism, and applies it to fault diagnosis based on multi-source heterogeneous features. To overcome the shortcomings of fixed scale convolution kernels in traditional convolutional autoencoder for feature extraction of multi-source information, the proposed hybrid model integrates a multi-scale information learning module into traditional convolutional autoencoder to construct MSCAE, enhancing its ability to extract features from heterogeneous multi-source information while considering feature information at different spatial scales to improve its noise suppression capability. Introduce sparse attention mechanism into MSCAE to improve the model's recognition rate of key fault features. At the same time, a quantum particle swarm optimization module is used to perform hyperparameter optimization on the hybrid model using chaos initialization and dynamic inertia weight strategy, improving the training and diagnostic efficiency of the model, and the problem of the randomness of diagnostic results caused by human selection of hyperparameters is also solved. Compared to most the current idea of building models based on one single factor, the hybrid model is constructed based on comprehensive factors such as multi-source heterogeneous feature extraction effectiveness, model diagnostic efficiency, and noise resistance, which is more comprehensive and applicable. The effectiveness and superiority of the model are verified through experiment and comparative studies. The superiority of the hyperparameter optimization algorithm was verified through ablation experiments.

In future research, we will attempt to apply the method on the diagnosis of gear and bearing faults under variable operating conditions such as variable speed, or the scenario where both variable load and variable speed occur simultaneously.