Nonlinear response of the generator rotor under the unbalanced electromagnetic force

2.1. Research target

The research target is the bearing rotor system of one Dongfang generator of 300 MW. Table 1 presents the main parameters of the bearing and its working condition.

For an actual generator rotor, it has been common practice that its physical model is so modeled that the contiguous rotor system can be reduced to a limited number of discrete systems with multiple degrees of freedom. Several methods can be employed in the modeling, including the lumped masses method, the FEM, the Rayleigh-Ritz method, and the Tomoshenko method, among which, the lumped masses method stands out as the best candidate because, in reality, additional factors related to the couple parts of the rotor, such as bearing, unbalance force, and unexpected shock, needs to reckoned with, and the lumped masses method can cater for this need better as against the other methods and can improve the convergence speed and accuracy.

In this paper, the actual generator rotor is modeled, using the lumped masses method, which requires that the mass of any segment be distributed to two adjacent nodes, with the rotor rigidity constant, in accordance with the principle of keeping the mass center unchanged, and that the mass and the moment of inertia of any segment keep constant before and after the model process. Because the actual generator rotor in this paper is symmetrical, we decided that each of the extended outer segments is of the same length as that of each inside segment. This is to take into account the influence of the external shaft coupling by factoring into the length parameters extended out of the bearings. So the generator rotor is modeled as 9 nodes and 8 segments, as shown in Fig. 1. The span of the actual rotor is 8000 mm, the total mass is 52810 kg, and the moment of inertia is 7365 kg·m². The total mass of rotor is divided into 9 lumped masses, and the parameters of the 8 segments are shown in Table 2.

Fig. 1Modeling rotor for the generator rotor system

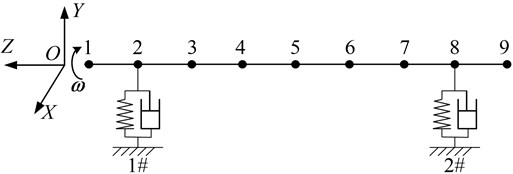
The nonlinear vibration responses of the above rotor-bearing system are calculated at the rated speed of 3000 rpm, and with varied electromagnetic forces due to distinct inter-turn short circuits. The values of the electromagnetic force under different inter-turn short circuit circumstances are shown in Table 3. The model of the generator rotor and the 0°, 90°, 180° positions of the inter-turn short circuit faults were shown in Fig. 4, [15].

Due to the symmetric rotor, a certain length of rotor segment is extended to the outer end of the bearing in order to make the stability threshold speed of generator rotor-bearing system approximate that of the modeling rotor. The bearings are installed in both ends, and have the same type and equivalent load. The dynamic oil film force can be obtained by solving the Reynolds equation with the finite-element method. The turbulence working condition with the Pan-Ng recommended turbulence factor is considered in the calculation process.

2.2. Calculation description

The vibration responses under the balanced and unbalanced conditions are studied in the paper. Under the balanced condition, the responses of the all nodes in the rotor system are caculated at the rated speed of 3000 rpm. Under the unbalanced condition, the responses of the all nodes and the nonlinear oil film force in different cases are calculated respectively, including the different situations, slight and serious short circuit faults. In this study, the slight and serious short circuit faults are defined by the ratio of short circuit winding turns to the total excitation turns. For slight short circuit, the ratio is low to 10 %, while for serious short circuit, the ratio is high to 25 %. The influences of the two distributed force mode on the vibration responses are studied. The electromagnetic force has two mode acted on the rotor, that is, the concentrated force acted on node 5 and distributed force acted on the node 3-7.

Table 3 presents the theoretical values of the electromagnetic forces under the rated speed in the 90° fault positions.

With the values of the electromagnetic force, the unbalanced eccentricity can be expressed as:

where, $E_{ei}$ is unbalanced eccentricity (m), $m$ is the mass (kg), $F_{ei}$ is electromagnetic force (N), $i=x$, $y$.

Then, the equivalent unbalance eccentricity can be defined as:

where, ${\rho }_{ei}$ is the equivalent unbalance eccentricity ($i=x$, $y$), $C$ is the radius clearance of bearings (mm).

Table 4 presents the equivalent unbalance eccentricity when the rated speed is 3000 rpm in the 90° fault positions, and distinct fault seriousness (slight and serious short circuit). The numerical values of ${\rho }_{ex}$ and ${\rho }_{ey}$ in Table 4 are the results of theoretical calculation.

Table 4 depicts the calculation list for the response analysis and the special unbalanced results. ${\rho }_{ex}$ and ${\rho }_{ey}$ are the unbalanced eccentricity originated from the electromagnetic force.

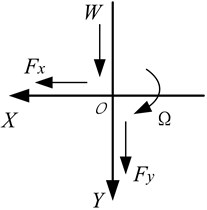
The coordinate system of the horizontal and vertical displacement $X$, $Y$ as well as bearing oil film force ($F_x$, $F_y$) involved in the caculation and analysis process is shown in Fig. 2. In Fig. 2, $W$ denotes the bearing load. $X$, $Y$, $F_x$, $F_y$ are dimensionless value, and the relative unit of $X$, $Y$ is bearing side clearance (C) while that of $F_x$, $F_y$ is $W$. The computing results of response include the displacement of periodic solutions $X_1$, $Y_1$, $X_2$, $Y_2$, $X_3$, $Y_3$, $X_4$, $Y_4$ (corresponding to nodes 2, 3, 4, 5 respectively in Fig. 1) and the waveform of $F_x$, $F_y$. The $X$-coordinate of the response is dimensionless time priod $T\text{,}$ whose unit is radian. While the unit of time is second, $T=\pi \mathrm{\Omega }t/30$. The maximum of $X$-coordinate is dimensionless priod for periodic solution. The $Y$-coordinate presents the nonlinear vibration response and corresponding rotor centerline orbit, the amplitude of response displayed by the $Y$-coordinate is the ratio of relative vibration response values which are relative to the static equilibium point (obtained by the calculation of bearing static point) to the bearing side clearance. The vertical axis presents the waveform of transient oil film force, $Y$-coordinate shows the ratio of the transient oil film force to bearing load.

Fig. 2Coordinate system (O – center of bearing)

3.1. Linear dynamics results

Tables 5 and 6 show the results of the static and dynamic characteristics for the sliding bearing at different rotational speed (800-4300 rpm).

Tables 5 and 6 present the theoretical values of the static and dynamic characteristics of the rotor when it is at different speeds. The dynamic characteristics of rotor are considered linear, and indexed by the 8 linear stiffness and damping coefficients ($K_{xx}$, $K_{xy}$, $K_{yx}$, $K_{yy}$, $C_{xx}$, $C_{xy}$, $C_{yx}$, $C_{yy}$). And in this case, the bearing load consists of only the rotor mass, and there is no added load and no unbalanced electromagnetic force. The first critical speed and the linear instability speed (expressed as the logarithmic decrement), shown in Figs. 3 and 4, are thus obtained by solving the following equation, which has taken into consideration of the system’s inherent vibration problems due to the multi-DOF bearing rotor system adopted:

where, $U={[x_1,y_1,...,x_N,y_N]}^T$ ($N$ is number of the nodes), and the coefficients matrix [$M$], [$C$], [$K$] is 2$N$×2$N$ matrix.

The 8$N$ eigenvalues, which are always the complex conjugate pairs, can be obtained by solving the corresponding eigenvectors of the above equations. Once whether the forward or reverse whirl occurs is determined, the eigenvalues $\gamma =-\sigma +i\omega$ under different speed conditions are obtained. The $\mathrm{\Omega }-\omega$ (speed – whirl speed) curve is made accordingly, and the intersection of the curve and the straight line $\omega =\mathrm{\Omega }$ is the critical speed.

For the multi-DOF bearing rotor system, set the value of the $j\text{order}$ eigenvalue as ${\lambda }_i=-{\sigma }_j+i{\omega }_j$, the corresponding logarithmic decrement can be noted as:

The minimum logarithmic decrement is defined as ${\delta }_{min}=\mathrm{m}\mathrm{i}\mathrm{n}\left({\delta }_i\right)$ under the different speed conditions. The linear instability speed can be defined as the one when ${\delta }_{min}=$0.

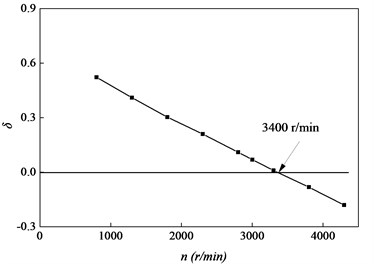
The whirl speed is shown as Fig. 3, while the Fig. 4 details the logarithmic decrement. As shown in the Fig. 4, the stability threshold of the generator rotor supported by the silding bearing is about 3430 rpm. The logarithmic decremen speed of shafting is 0.0695 at the working speed (3000 rpm). The error between the real first critical speed which is about 1280 rpm and the designed one provided by the Company is approximately 5 %.

Fig. 3Whirl speed vs. speed

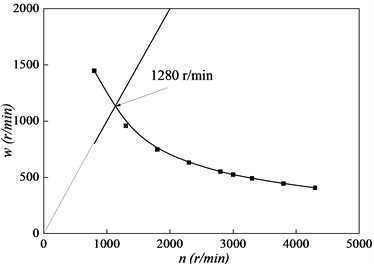
Fig. 4Logarithmic decrement vs. speed

3.2. Nonlinear vibration response analysis for the generator rotor at the rated speed

Fig. 5 displays the rotor centerline orbit of the generator rotor at the normal rotational speed of 3000 r/min. The relative vibration response values shown in Fig. 5 are relative to the static equilibrium position (obtain by the calculation of bearing static characteristics). Fig. 6 depicts the oil film force waveform for the transient process. Figs. 5 and 6 depicts the nonlinear vibration response results when the nonlinear oil film force works under normal condition. This should not be viewed as linear analyses. The nonlinear government equation is expressed as Eq. (1) [15], where the $f_x$ and $f_y$ denote the oil film force components in the horizontal and vertical directions respectively.

Fig. 5Rotor centerline orbit under normal condition

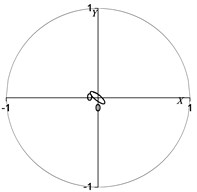
a) Node 2

b) Node 3

c) Node 4

d) Node 5

In order to analyse the stability of the system, it is necessary to conduct FFT of the vibration response in stable stage and to obtain the maximum and minimum of the steady-state solutions. The results of the vibration response and oil fim force are shown in Table 7. The harmonic component of the FFT result for the steady-state solutions (vibration response and oil film force at different nodes) can be seen in Table 8.

Fig. 6Oil film force under normal condition

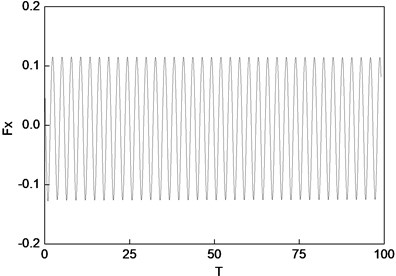
a) Horizontal direction

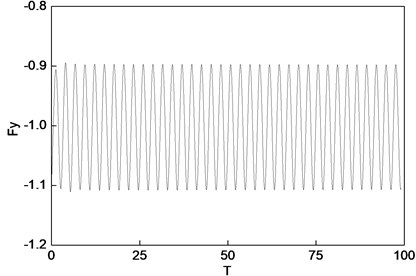
b) Vertical direction

3.3. Results analysis and discussion

1) The result shows that the first critical speed of the generator rotor is about 1280 rpm. Comparison to the first critical speed provided by the designed company (1347 rpm), the error is approximately 5 %. The critical speed is meet to requirement of distancing from working speed over 500 rpm. The linear stability threshold speed of the generator rotor supported by the sliding bearing is about 3430 rpm. The logarithmic decrement is 0.0695 at the working speed of 3000 rpm. The stability margin of the generator rotor system at rated speed is low. So, once the excitation winding inter-turn short circuit faults occur, the system is possible to be unstable.

2) The vibration response results show the generator system with considering the nonlinear oil film force effect have steady periodic solutions, the frequency of response is the working frequency and steady motion state is periodic motion. Vibration peak in the bearing situation (namely node 2) is 0.0793 (in horizontal direction), 0.0070 (in vertical direction); and the vibration peak in symmetric center of rotor (namely node 5) is 0.1550 (in horizontal direction), 0.1353 (in vertical direction). Because of low stability margin, the system will be possible to produce self-excited vibration or forced vibration once suffered from large disturbance, such as transient exogenous shock, electromagnetic force caused by inter-turn short circuit and steam seal expiration. In the successive study, the nonlinear vibration of the generator rotor under the different inter-turn short circuit cases will be analyzed in detail, the vibration characteristics under the different short circuit faults will be obtained.

4.1. Concentrated force mode

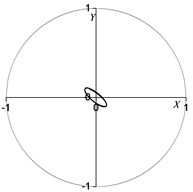
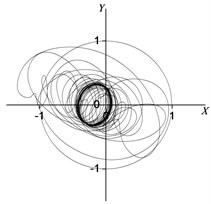
The rotor non-linear vibration model of the coupling of the unbalanced electromagnetic force and nonlinear oil film force has been published in [15]. In this paper, based on the above model, we intend to analyze the rotor’s nonlinear vibration behavior under different inter-turn short circuit mode conditions. In [15], the non-linear vibration model was validated by the experimental test. Fig. 7 shows the rotor center orbit of vibration response generated by the concentrated electromagnetic force mode under 90° (acted at the node 5) position serious fault. Fig. 8 depicts the oil film force waveform of response during the transient process.

Fig. 7Rotor centerline orbit under 90° position serious fault (concentrated force)

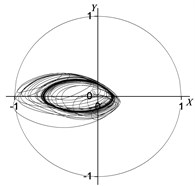
a) Node 2

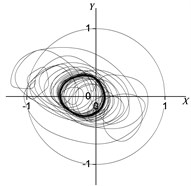
b) Node 3

c) Node 4

d) Node 5

Fig. 8Oil film force under 90° position serious fault (concentrated force)

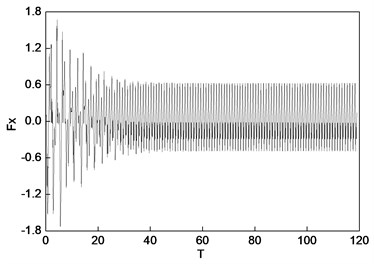
a) Horizontal direction

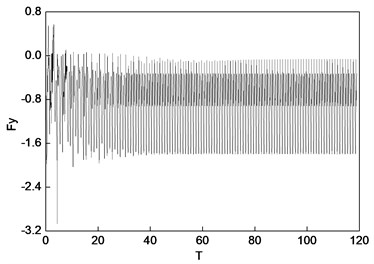
b) Vertical direction

The FFT for the vibration response in the steady motion state is conducted under the 90° position serious fault condition with the concentrated force mode, and the maximum, minimum displacements and amplitude of the steady-state solution (for nodes 2, 3, 4, 5 and oil film force) are listed in Table 9. The harmonic components of the vibration response in nodes 2, 3, 4, 5 and the oil film force are shown in Table 10. As a compative study, the FFT and displacement harmonic component analysis for the vibration response in the stable stage under 90° position slight fault is also provided in the paper, as shown in Tables 11 and 12.

It can be seen in Fig. 7 and Fig. 8 that when vibration orbit reach steady-state solutions, the state of motion is synchronous whirl. Fig. 7 details that the steady-state rotor centerline orbit is the quasi-periodic motion. The amplitude of the steady-state solutions and the FFT result are displayed in Table 9 and Table 10, and the results illustrate that steady motion is periodic with the period of $T$, and only sychronized whirl exists in the system. The horozontal and vertical $\mathrm{\Omega }$ sychronized component in the bearing situation are 0.37597 and 0.16836 respectively, while that in the rotor center is 0.34575 and 0.54622. Table 8 and Table 9 also suggest that due to the nonliear electromagnetic force caused by the inter-turn short circuit faults, the vibration of rotor display the nonlinear characteritics. The amplitude values of node 2, 3, 4, 5 in horizontal and vertical directions increase by 425 %, 168 %, 80 %, 28 % and 2702 %, 186 %, 164 %, 129 % respectively compared the values under the nomal conditions. Meanwhile, the horizontal and vertical amplitude of oil film force increase by 367 %, 728 % respectively because of the electromagnetic force.

Comparing the slight short circuit fault cases with the serious cases (shown in Tables 11 and 12) under 90° position, the state of motion transforms from the quasi-periodic motion to the synchronous whirl. The motion state whose main and secondary composition of vibration response is the response of the self-excited vibration and the forced vibration respectively converts into the sychronized whirl. As the unbalanced force caused by the short circuit increases, the vibration amplitude of the bearing situation rises by 46 % (in horizontal direction) and 30 % (in vertical direction). While there is a decrease of 19 % (in horizontal direction) and a increase of 12 % (in vertical direction) in the vibration amplitude of rotor center where the centrated force acting on (namely node 5). The oil film force amplitude increased by 32 % (in horizontal direction) and 73 % (in vertical direction). Although the variation law of vibration amplitude is complicated, sychronized whirl aroused by the self-excited vibration increases all the time as the severity of short circuit fault rises. In contrast with the slight short circuit case, under serious fault, the self-excited vibration amplitude of the bearing situation rise by 82 % (in horizontal direction) and 76 % (in vertical direction). While there is an increase of 55 % (in horizontal direction) and 73 % (in vertical direction) in the self-excited vibration amplitude of the rotor center (namely node 5) where the centrated force is acting on. And the oil film force amplitude increased by 29 % (in horizontal direction) and 43 % (in vertical direction).

4.2. Uniform force mode

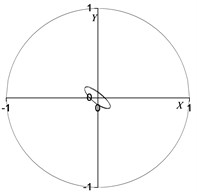
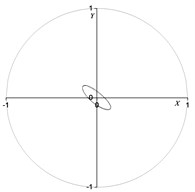
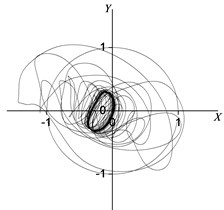
Fig. 9 depicts the rotor center orbit of the vibration response generated by the uniform electromagnetic force mode under 90° (acted at the node 2, 3, 4, 5, 6, 7) position serious fault. Fig. 10 depicts the oil film force waveform during the transient process.

Fig. 9Rotor centerline orbit under 90° position serious fault (uniform force)

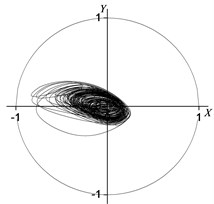
a) Node 2

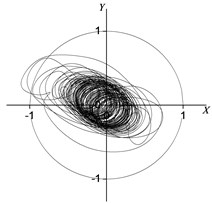
b) Node 3

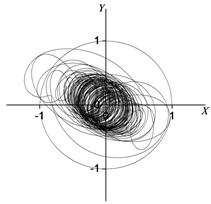
c) Node 4

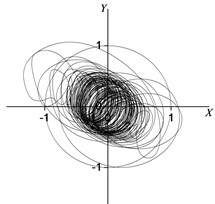
d) Node 5

The FFT for the vibration response in the steady motion state is conducted under the 90° position serious fault condition with the uniform force mode, and the maximum, minimum displacements and amplitude of the steady-state solution (for nodes 2, 3, 4, 5 and oil film force) are listed in Table 13. The harmonic components of the vibration response in nodes 2, 3, 4, 5 and the oil film force are shown in Table 14. As a compative study, the FFT and displacement harmonic component analysis for the vibration response in the stable stage under 90° position slight fault with the uniform force mode, is also provided in the paper, as shown in Tables 15 and 16.

Fig. 10Oil film force under 90° position serious fault (uniform force)

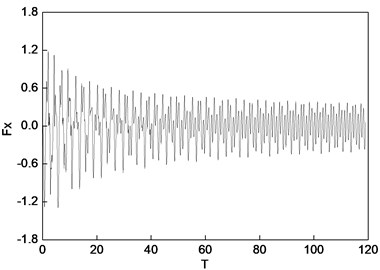
a) Horizontal direction

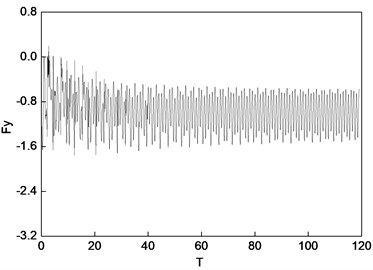
b) Vertical direction

It can be seen in Fig. 9 and Fig. 10 that when vibration orbit reach steady-state solutions, the state of motion is the quasi-periodic motion. Fig. 9 details that the steady-state rotor centerline orbit is the quasi-periodic motion. The amplitude of steady-state solutions and results of FFT are displayed in Table 13 and Table 14. The results illustrate that though the steady-state solutions are composed of amplitude of vibration forced by electromagnetic force and amplitude of self-excited vibration, the main component is the response of self-excited vibration which is different under concentrated force mode under 90° position serious fault. The horizontal and vertical harmonic components from the forced vibration components (0.35$\mathrm{\Omega }$) in the bearing situation (node 2) are 69 % and 49 % less than the harmonic component of $\mathrm{\Omega }$ respectively. While the horozontal and vertical harmonic components due to the forced vibration in the rotor center (node 5) are 53 % and 71 % less than harmonic component of $\mathrm{\Omega }$ respectively. The horozontal and vertical oil film force harmonic components are 62 % and 80 % less than harmonic component of $\mathrm{\Omega }$ respectively.

The harmonic component of the forced vibration gained from the FFT results is $\omega =$0.35$\mathrm{\Omega }=$1050 rpm, about 1/3 order harmonic component of $\mathrm{\Omega }$ (1000 r/min). It can be concluded that the steady motion is 1/3 order subharmonic resonance, and the vibration is mainly composed of 1/3 order harmonic component and first harmonic component. It can be seen from the analysis result that the inter-turn short circuit under 90° position in generator rotor is likely to excite low frequency subharmonic resonance whose frequency is close to 1/3 of rated speed.

Comparing the slight short circuit fault cases with serious cases (shown in Tables 15 and 16) under 90° position, the state of steady motion transforms from the quasi-periodic motion to the subsynchronous resonance as the severity degree of short circuit increasing, inflecting in the decline of harmonic frequency (decrease from 0.41$\mathrm{\Omega }$ to 0.35$\mathrm{\Omega }$). The main composition in steady solution changes from the forced vibration component to self-excited vibration component. Compared with slight short circuit, under serious fault, the vibration amplitude of the bearing situation (namely node 2) decreases by 26 % (in horizontal direction) and 31 % (in vertical direction). While there is a decrease of 44 % (in horizontal direction) and 25 % (in vertical direction) in the vibration amplitude of the rotor center (namely node 5). And the oil film force amplitude declineds by 41 % (in horizontal direction) and 18 % (in vertical direction). The result shows that as the electromagnetic unbalanced force increases, the vibration of system is defined and vibration amplitude beomes smaller. However the main reason is that forced vibration component in vibration composition decreases while the self-excited component rises all the time with the short fault becoming more serious. Compared with the slight short circuit, the self-excited vibration amplitude of the bearing situation (node 2) rises by 103 % (in horizontal direction) and 111 % (in vertical direction) under serious fault. While there is a increase of 62 % (in horizontal direction) and 63 % (in vertical direction) in the self-excited vibration amplitude of rotor center (namely node 5). And the self-excited vibration component of oil film force rises by 61 % (in horizontal direction) and 67 % (in vertical direction). Compared with slight short circuit, under serious fault, forced vibration response declined as the severity degree of short circuit increases. The amplitude of forced vibration decreases by 76 % (in horizontal direction) and 75 % (in vertical direction) in bearing situation (namely node 2) and rotor center (namely node 5). The oil film amplitude of forced vibration decreases by 79 % (in horizontal direction) and 76 % (in vertical direction).

The vibration amplitude in different nodes caused by electromagnetic force inspired by the inter-turn short circuit under 90° position are analysed in cases where electromagnetic force are treated as concentrated force and uniform force mode respectively, and the result and comparision are shown in Table 17, where the difference:

It can be seen from the Table 17 that, the maximum of difference is 52 % (in horizontal direction) and 33 % (in verticle direction) between the two the force mode of electromagnetic force. It is may because that in the process of the nonlinear vibration, the larger unbalance electromagnetic force is denoted as the concentrated force mode causes the synchronous whirl and the frequency of synchronous whirl component is $\mathrm{\Omega }$, while the frequency of harmonic component under the uniform force mode is 0.35$\mathrm{\Omega }$.The analysis also suggests that the value of vibration response is smaller while the electromagnetic force are treated as the concentrated force.

For the two cases where the electromagnetic force are treated as the concentrated force mode and the uniform force mode respectively, Table 18 gives the comparison result for the steady solution harmonic component of vibration response in different nodes. In the table, the difference:

The main harmonic component and difference of each node vibration shown in Table 18 suggest that the difference of the self excited vibartion amplitude decreases as the distance from node to the position where the concentrated force acting on becomes smaller. However, applying uniform unbalanced force mode at the node 5 (where the concentrated force acting on) would cause larger self-excited vibration. The response in the bearing situation (namely node 5) under the concentrated force mode is 91 % (in horizontal direction) and 86 % (in vertical direction) larger than that under the uniform force mode. The difference of response in node 4 is 3 % (in horozontal direction) and 9 % (in vertical direction) larger respectively; and the response in node 5 is 35 % (in horizontal direction) and 12 % (in vertical direction) smaller respectively; while the difference of oil film force response is 36 % (in horizontal direction) and 51 % (in vertical direction) lager.