Abstract
The inside oblique angle between the vertical plane and the arch rib has been shown to be one of the main factors influencing dynamic properties of long-span steel-box basket-handle arch bridges. Details related to the extent, that the inside oblique angle influenced the dynamic characteristics and the seismic response of the arch bridge under the combined longitudinal and vertical seismic excitation and under the combined lateral and vertical seismic excitation, were reported herein. Four oblique angles (0°, 3°, 4.8° and 6°) were selected based on the arch ribs height and bridge deck width. Findings suggested that a larger inside oblique angle increased the structural stiffness and thus the part internal forces when subjected to seismic excitation. These findings also showed that, when similar structures were designed and seismic considerations were warranted, a suitable inside oblique angle to mitigate dynamic effects should be selected only using a comprehensive analysis. At the same time, traveling wave effect analysis indicated that it couldn’t be ignored when calculating the seismic response of long-span steel-box basket-handle arch bridges.
1. Introduction
Basket-handle arch bridges have gradually gained popularity due to their attractive appearance and the contribution of their leaning arch ribs to their structure stability. To date, three types of basket-handle arch ribs have been designed and constructed: concrete [1], concrete-filled steel tubes [2-4], and steel-box [5-7]. Of the three, steel-boxes have become the main rib form used today, and corresponding research on their performance has mainly concentrated on highway structures with less focus on railway bridges, even though basket-handle railway bridges are being designed and constructed. Due to the large live loads these narrow railway structures could experience, the possibility that these loads would traverse them at high speeds and the increasing spans, the seismic performance of steel-box basket-handle railway arch bridges should be given more attention.
The characteristics of steel-box basket-handle arch bridges implied that the vibrations of such an arch bridge were mainly affected by the span to rise ratio, lateral bracing, support conditions, the inside oblique angle of ribs, etc. As the change of inside oblique angle of ribs directly influences the structural mechanical properties, it is helpful to design these types of bridge by analyzing the change regulation of ribs. The Zhaoqing Xijiang River Bridge, a long-span steel-box basket-handle arch bridge on the Nanning-Guangzhou Railway, was selected as the study object, and the influence of different inside oblique angles (0°, 3°, 4.8°, 6°) on natural vibration characteristics and seismic response was analyzed to obtain a referential value to similar engineering design.
2. Description of the bridge
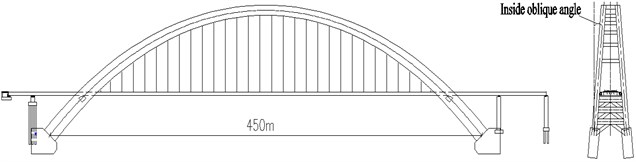
The Nanning-Guangzhou Railway carries a mixture of passenger and freight at speeds up to 250 km/h, and is across the Xijiang River near the city of Zhaoqing via the Zhaoqing Xijiang River Bridge. This bridge is a half-through steel-box basket-handle arch bridge having a main span of 450 m, which classifies it as the longest-span steel-box basket-handle railway arch bridge in the world. A simplified elevation and side view of the structure is shown in Fig. 1 and its basic parameters consist: a span to rise ratio of 4; an arch-axis coefficient of 1.8; an inside oblique angle of 4.8° between the vertical plane and the arch rib; a distance of 71.7 m from the deck to the vault; a lateral distance of 34.0 m between arch rib centers on each springing; and a lateral distance of 15.17 m between arch rib centers at the vault.
The bridge arches were each founded on arch springings measuring 12.0 m wide, 23.4 m high, and 26.6 m in the lateral direction. Each steel arch rib had a variable cross-section, consisting of steel box of 4.0 m wide, and 8.0 m high at vault section and 15.0 m high at springing section. One arch was braced to another by 18 bracing sets, including 12 sets of flat steel-box braces located above the deck system and 6 sets of K-type transverse-braces located below the deck.
The floor system consisted of two main longitudinal steel-box beams of 3.0 m high and 2.0 m wide and several transversal steel beams with box type section at supporting sections and “I” type at other sections, supporting a reinforced concrete bridge deck. The deck slab was a 200 mm thick C50 reinforced concrete precast slab which was set on a 200 mm thick cast-in-place reinforced concrete layer. Precast slabs, which formed a semi-floating bridge deck structure, were laterally and longitudinally jointed by shrinkage-compensating steel-fiber reinforced concrete.
Fig. 1Elevation and side view of Zhaoqing Xijiang River Bridge
3. Analysis of dynamic characteristics
3.1. Finite element model
According to the dimensions of the components of the Zhaoqing Xijiang River Bridge as indicated in the detailed design drawings, a model of the bridge was firstly established using a commercial software. In addition, in light of the complexity of this bridge, the spatial element models of the decks and beams were built using customised sections to actually reflect the real spatial stress state in this bridge. This model utilized customised sections to accurately depict the complexity of key structural elements. Variable steel-box-section arch ribs were simulated using two-noded, 3-D elastic beam elements with tension, compression, torsion, and bending capabilities varying dimension with other primary steel superstructure members, including the beams supporting the railway deck and bracing between the arches. The deck hanger simulated by the 3-D elastic rod element having the unique feature of a bilinear stiffness matrix resulting in a uniaxial tension-only or compression-only element, and the concrete deck was represented using the elastic shell element has both bending and membrane capabilities. The material parameters and section properties are given in [8].
Moreover, the secondary dead load (like rail, ballast etc.) on the bridge was simulated by increasing the density of the bridge deck. The whole bridge was divided into 1,496 nodes and 1,356 units. When the two arches are inclined towards each other one would expect the bridge to become laterally stiffer, so the inside oblique angle of arch rib was either 0°, 3°, 4.8°, or 6°, while other materials, section features, boundary conditions, etc. were unchanged. Representative finite element models of the Zhaoqing Xijiang River Bridge, ones having inside oblique angles of 4.8°and 0°, are shown in Fig. 2. The boundary conditions were: arch rib and deck system were intersected by beams; beams were connected to the primary longitudinal beam of the floor system by supports; arch ribs were consolidated with arch supports; deck hangers were linked to the primary longitudinal beam. The mode damping ratio of this bridge was estimated to be 0.03.
Fig. 2Finite element models of Zhaoqing Xijiang River Bridge with different inside oblique angles

a) Inside oblique angle: 4.8°
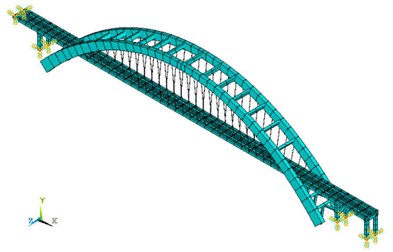
b) Inside oblique angle: 0°
3.2. Dynamic characteristics
The initial series of finite element analyses were completed to study dynamic characteristics so that the effect of treating sparse matrices was obtained using the block Lanczos method [9], and 200 natural frequencies and mode shapes were obtained for each model with one special inside oblique angle. Three classical mode shapes corresponding to the inside oblique angle of 4.8° were shown in Fig. 3.
Fig. 3Mode shapes of Zhaoqing Xijiang River Bridge with the inside oblique angle of 4.8°

a) 1st mode (vertical view): 0.4291 Hz

b) 1st mode (side view): 0.4291 Hz
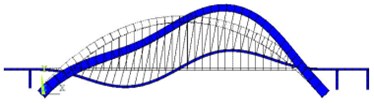
c) 2nd mode (vertical view): 0.4496 Hz

d) 2nd mode (side view): 0.4496 Hz

e) 3rd mode (vertical view): 0.5354 Hz

f) 3rd mode (side view): 0.5354 Hz
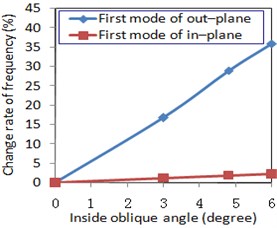
The influence of oblique angle on natural frequencies is demonstrated via the plot in Fig. 4, which plots frequency verses mode number for ten mode shapes. Examination of the results revealed differences for how changes in oblique angle affected vertical and lateral bending modes and Fig. 5, which compares rates of change of their fundamental frequencies as oblique angles change, demonstrates these differences. Based on Figs. 4 and 5, the influence of inside oblique angle on dynamic characteristics, for the angles that were studied, can be summarized as follows:
1) The spatial torsional stiffness of the arch ribs increased by tilting the arch. This was attributed to the fact that the arch torsion was mainly generated by independent vertical displacements of the two arch ribs. Since the lateral bracings of this titling basket-handle arch were shorter than that of a typical parallel arch, the restraint degree and the corresponding spatial torsional stiffness developed by this titling basket-handle arch were larger.
2) The inside oblique angle exerted different influences on the natural vibration modes of this long-span steel-box basket-handle arch bridge. It exerted larger influences on the out-of-plane vibration, and lesser influences on the in-plane vibration. Moreover, the influences on the out-of-plane vibration intensified as the inside oblique angle increased. For example, the out-of-plane fundamental frequency grew by 16.8 %, 29 %, and 36 % at inside oblique angles of 3°, 4.8°, and 6° (compared to that at an inside oblique angle of 0°, shown in Fig. 5) respectively. This result suggested that an increased inside oblique angle strengthened the out-of-plane stiffness of long-span steel-box basket-handle bridges and, in turn, enhanced the out-of-plane stability.
Fig. 4Influence of inside oblique angle on natural frequencies
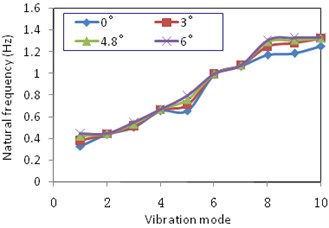
Fig. 5Influence of inside oblique angle on the rate of change of fundamental frequency
4. Seismic analysis
4.1. Seismic excitation
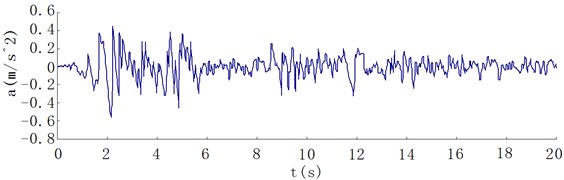
A seismic record, the North-South seismic wave from El-Centro, from a similar geological environment, likely magnitude, and spectral characteristics as the bridge site was used as the seismic input, in which the time-step was 0.02 s and the total time length analysed was 20 s. Due to the Zhaoqing Xijiang River Bridge being located in a seismic intensity area of degree 6 [10], the peak ground acceleration (PGA) of the El-Centro wave was adjusted to be 0.055 g to obtain the reasonable seismic input, as shown in Fig. 6, of the bridge.
Since the foundations of the bridge were mainly constructed on bedrock, the influences of the interaction of the bridge base and its foundation on its the seismic response were neglected.
Fig. 6Adjusted El-Centro seismic wave
4.2. Influences of inside oblique angle on seismic response
The influence of inside oblique angle on the seismic response of long-span steel-box basket-handle bridges was analyzed. The uniform excitation history analysis method was applied to the cases of inside oblique angles of 0°, 3°, 4.8°, and 6° to obtain the maximum internal force and displacement of this bridge under longitudinal plus vertical and lateral plus vertical excitations respectively. The internal force in the structure was mainly investigated in four sections: the arch springing, at intersections of arch rib and bridge deck, at ¼-span in the arch rib, and in the vault itself, while displacement controlled the sections of the vault and ¼-span points of the arch rib. The seismic responses of the bridge under the longitudinal plus vertical excitation are shown in Fig. 7, while those under lateral plus vertical excitation are shown in Fig. 8. By comparing these data, the following conclusions are drawn:
1) Under longitudinal plus vertical excitation, the maximum seismic response was generated by the internal force on the arch springing at inside oblique angles of 0°, 3°, 4.8°, and 6°. An increased inside oblique angle further increased the axial force and in-plane bending moment of all typical sections under seismic action. However, the out-of-plane bending moment caused by seismic excitation appeared to be governed by a different set of parameters: with increased inside oblique angle, it decreased.
Fig. 7Longitudinal and vertical excitation effect for internal force and displacement
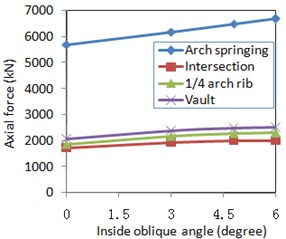
a) Axial force
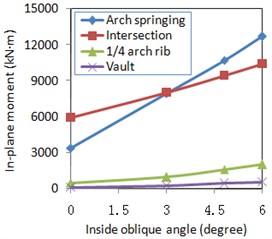
b) In-plane bending moment
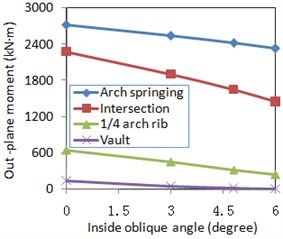
c) Out-of-plane bending moment
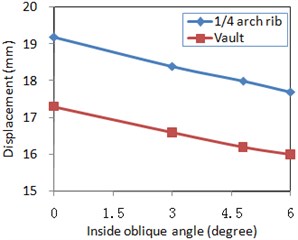
d) Longitudinal displacement
2) Under longitudinal plus vertical excitation, an increased inside oblique angle reduced all displacements caused by seismic action. In addition, the arch rib displacement caused by longitudinal plus vertical horizontal seismic action was concentrated in the longitudinal and vertical directions, and less so in the lateral direction.
3) Under lateral plus vertical excitation, the maximum axial force in the arch rib occurred near the arch springing at inside oblique angles of 0°, 3°, 4.8°, and 6°. An increased inside oblique angle increased the axial force on each key section of the arch rib. However, related in-plane and out-of-plane bending moments were less sensitive to the inside oblique angle. Besides, different sections showed different seismic responses. These responses were mainly reflected as increased in-plane and out-of-plane bending moments near the vault and decreased in those near arch springing sections.
4) Under lateral plus vertical excitation, the longitudinal and vertical displacements of typical sections of the arch rib were less sensitive to changes in inside oblique angle. Moreover, different sections showed different seismic responses. However, when the inside oblique angle continued increasing, the lateral displacement on the vault and ¼-span arch rib sections decreased.
Fig. 8Lateral and vertical excitation effect for internal force and displacement
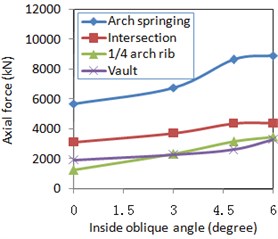
a) Axial force
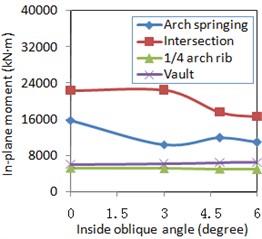
b) In-plane bending moment
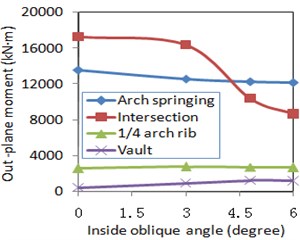
c) Out-of-plane bending moment
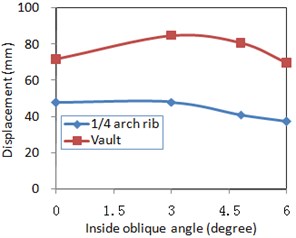
d) Lateral displacement
4.3. Travelling wave effects
Travelling wave effect is a special type (the same wave but arriving at different times) of earthquake ground motion variation [11]. For a long-span steel-box arch bridge with multiple supports along the longitudinal direction of the structures under excitation, there exist time-lag and a wave phase difference between different excitation points due to limited propagation velocity of earthquake wave: this resulted in travelling wave effects [12]. The influence of travelling wave effects on structural response was analyzed using the large mass method [13], which incorporated the following assumptions:
1) The adjusted El Centro seismic wave was assumed to be the input.
2) Seismic wave propagation occurred along the bridge, and only the longitudinal input was considered when calculating the travelling wave effect.
3) There was no attenuation or spectral characteristic change when seismic waves propagated between the arch springs.
4) The effects of pile soil interaction were deemed negligible.
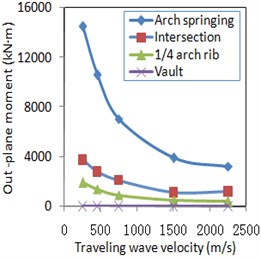
To consider the different travelling wave velocity effects on the structural seismic response, travelling wave velocities of 250 m/s, 450 m/s, 750 m/s, 1500 m/s, and 2250 m/s were used, and the corresponding phase differences between the arch springs were 1.8 s, 1.0 s, 0.6 s, 0.3 s, and 0.2 s, respectively. The seismic internal force and displacement responses of the Zhaoqing Xijiang River Bridge (inside oblique angle 4.8°) under different travelling wave velocities and uniform excitation are compared in Figs. 9-11, respectively.
Fig. 9Travelling wave velocity effect for internal force
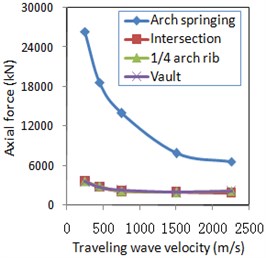
a) Axial force
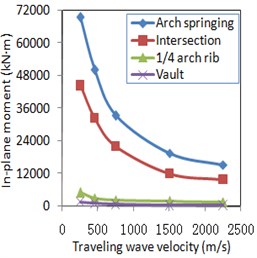
b) In-plane bending moment
c) Out-of-plane bending moment
Fig. 10Travelling wave velocity effect for displacement history
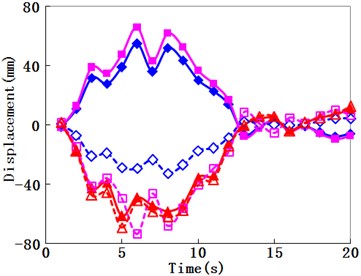
a) Traveling wave velocity is 250 m/s
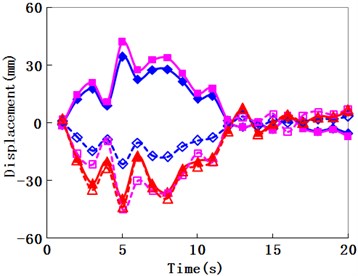
b) Traveling wave velocity is 450 m/s

c) Traveling wave velocity is 750 m/s
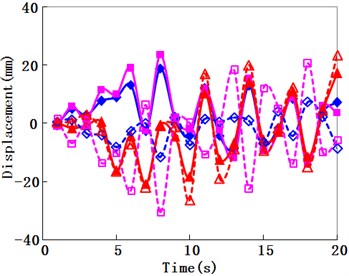
d) Traveling wave velocity is 1500 m/s
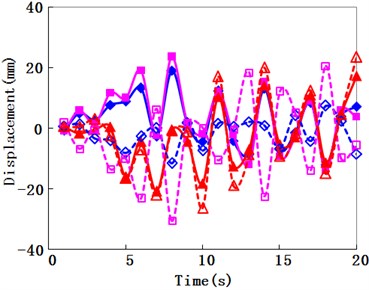
e) Traveling wave velocity is 2250 m/s

In Fig. 9, the seismic internal forces of arch spring, intersection and ¼-span point on the arch rib section were the maximum ones of the corresponding symmetry positions, respectively. Compared with uniform excitation, the seismic internal force responses of typical sections of the arch rib considering travelling wave effects increased significantly. At the same time, all internal forces in the arch rib decreased in cases with an increased travelling wave velocity, and when the velocity increased beyond a certain value, the travelling wave effect gradually decreased and tended to a uniform excitation result.
In Fig. 10, almost all of the maximum displacements occurred at the times between 5 s and 10 s. In this range, as for the longitudinal displacements, the response directions of the corresponding symmetry positions were opposite to each other. When the travelling wave velocities increased, this trend became feebler, and the results of the corresponding symmetry positions were both becoming less to be close to that of uniform excitation. When the lateral displacements were concerned, although the responses of the corresponding symmetry positions were different, they seemed not to be significantly opposite. When the travelling wave velocities increased, these results were also becoming less to be close to that of uniform excitation.
In Fig. 11, the envelope values of the displacement history shown in Fig. 10 were drawn as the similarly as that of Fig. 9. When compared with uniform excitation, the seismic displacement responses of typical sections of the arch rib considering travelling wave effects increased significantly. Furthermore, all displacements of the arch rib decreased in cases with an increased travelling wave velocity, and when the velocity increased beyond a certain value, the travelling wave effect gradually decreased and tended to a uniform excitation result. Those change trends in Fig. 11 were the same as that of Fig. 9.
Therefore, the essence of Figs. 9-11 was the same, and finally showed that the travelling wave effect was significant and could not be ignored in the analysis of the seismic response of such a long-span steel-box basket-handle arch bridge.
Fig. 11Travelling wave velocity effect for displacement
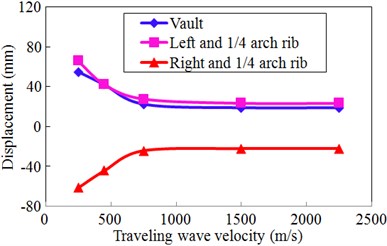
a) Longitudinal displacement
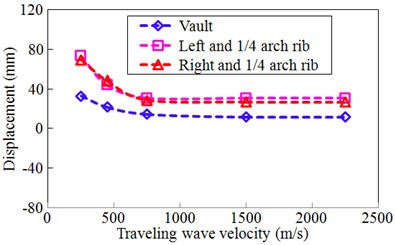
b) Lateral displacement
5. Discussions
Figs. 4 and 5 showed that a larger inside oblique angle of the arch rib increased the in-plane stiffness and the out-of-plane stiffness of the long-span arch bridge, and thus the corresponding vibration periods became shorter, especially for the out-of-plane ones.
When those bridges with different inside oblique angles were under the longitudinal plus vertical excitation, the longitudinal displacements of the arch rib were naturally decreased along with a larger inside oblique angle as shown in Fig. 7(d) based on the relationships between the structural dynamic characteristics and the earthquake characteristics. Similarly, the axial force and the in-plane bending moment would increase just as shown in Fig. 7(a) and 7(b). However, as the inside oblique angles were not very large, the longitudinal plus vertical earthquake would not significantly excite the out-of-plane modes, which resulted in a little out-of-plane bending moment as shown in Fig. 7(c).
When those bridges with different inside oblique angles were subjected to the lateral plus vertical excitation, there were no regular change rules for the lateral displacements of the arch rib, which were influenced by the higher modes, along with a larger inside oblique angle as shown in Fig. 8(d). Because a larger inside oblique angle of the arch rib increased the in-plane stiffness and the out-of-plane stiffness of the long-span arch bridge, it resulted in the larger axial force of the arch rib as shown in Fig. 8(a). As the out-of-plane bending moments were significantly influenced by the higher modes, their values related to different parts of the arch rib changed differently from each other as shown in Fig. 8(c) when the inside oblique angle increased. Under the lateral plus vertical excitation, the in-plane bending moment and the out-of-plane bending moment were coupled with each other, and they had the same change trend as the inside oblique angle increased.
When the travelling wave acted on the bridge with the inside oblique angle of 4.8° in the longitudinal direction, the similar modes as well as the mode 2 in Fig. 3 were firstly excited. Therefore, as for the longitudinal displacements in Fig. 10 and Fig. 11(a), the response directions of the corresponding symmetry positions were opposite to each other. As the traveling wave velocity was less, the travelling wave effects were significant which also resulted in the larger axial force and the larger in-plane bending moment as shown in Figs. 9(a)-(b). Due to the strong links of the lateral bracings between two arch ribs, the lateral mode shapes of the two arch ribs had the same direction for each mode, and thus the lateral displacements in Fig. 10 and Fig. 11(a) changed almost in the same directions.
After the seismic responses under the uniform excitation and the travelling wave were compared with each other, the former response was significantly awful. If there was an earthquake wave with a little velocity travelling along the longitudinal direction of such a long-span steel-box basket-handle arch bridge, the traveling wave effects could not be ignored in the analysis of the seismic response.
In summary, although a larger inside oblique angle of the arch rib increases the out-of-plane stability, it sometimes makes the larger internal force and displacement. Based on the general equal displacement rule [14], if one structure is only slightly damaged by the earthquake, its seismic response characteristics are almost the same with the elastic seismic response. Therefore, the rules obtained by this paper are conditionally applicable to the similar arch bridges in the area with strong ground motion. As the seismic response of one moderately or severely damaged structure is absolutely different from the elastic seismic response. It is necessary to study on the plastic response of the similar arch bridge to evaluate its seismic performance through incremental dynamic analysis in the future.
Moreover, the rules in this paper are qualitative rather than quantitative. Many investigations such as considering the structure-soil interactions, the influence of higher modes, the detailed multi-point earthquake calculation methods [15] and under many earthquake excitations [16], etc, for such a long-span steel-box handle-basket arch bridge should be carried out in the future.
6. Conclusions
This study investigated the influences of inside oblique angle on the dynamic characteristics and seismic response of a long-span steel-box handle-basket arch bridge. A larger inside oblique angle of the arch rib increases the out-of-plane stiffness of the long-span arch bridge and thus enhances its out-of-plane stability. However, it exerts little influence on the in-plane stiffness. This rule influences the dynamic characteristics and the corresponding seismic response of the arch bridge. When subjected to the same uniform earthquake, the inside oblique angle sometimes makes the larger internal force and displacement, which is against the structure design. Furthermore, the travelling wave effect is significant and cannot be ignored in the analysis of the seismic response of such a long-span steel-box basket-handle arch bridge. Fortunately, this arch bridge is located in a little earthquake area, and the seismic response will not control the structure design when compared to other actions.
References
-
Wang Y., Chen H., Yang L. Analysis on the spatial dynamic performance of basket-handle bridge. World Earthquake Engineering, Vol. 25, Issue 2, 2009, p. 72-75.
-
Du S. Y., Chen H., Yin X. G., Sun Z. Seismic response analyses of a concrete-filled steel tubular arch bridge. Proceedings of the 3rd International Conference on Earthquake Engineering, Nanjing, China, 2004.
-
Yan W. M., Li Y., Chen Y. J. Seismic testing of a long-span concrete filled steel tubular arch bridge. Key Engineering Materials, Vol. 456, 2011, p. 89-102.
-
Zhao C. H., Zhou Z. X. The random response of long-span concrete-filled steel-tube basket-handle bridge under multi-dimensional seismic excitations. Journal of Earthquake Engineering and Engineering Vibration, Vol. 25, Issue 3, 2005, p. 87-92.
-
Tian Z. C., Chen C. S., Zheng W. G. The modal test on the steel-box handle-basket arch bridge. Journal of Vibration and Shock, Vol. 23, Issue 2, 2004, p. 44-49.
-
Wang J. J., Qin R., Xie K. Z. Analysis method about the seismic response of long-span steel-box basket-handle bridge. Journal of Lanzhou University of Technology, Vol. 34, Issue 1, 2008, p. 102-105.
-
Zhang G. Y., Liu J. M. Testing study on the dynamic properties of Shanghai Lupu Bridge in China. Journal of Vibration and Shock, Vol. 27, Issue 9, 2008, p. 167-170.
-
Zhai J. P. Analysis on the dynamic properties of Zhaoqing Xijiang Bridge. Journal of Railway Science and Engineering, Vol. 8, Issue 3, 2011, p. 13-17.
-
Nour-Omid B., Clough R. W. Block Lanczos Method for dynamic analysis of structures. Earthquake Engineering and Structural Dynamics, Vol. 13, Issue 2, 1985, p. 271-275.
-
TB 10621-2009. Code for Design of High Speed Railway. Ministerial Standard of People of Republic of China, Beijing, China, 2009.
-
Xu Y., Lee G. C. Travelling wave effect on the seismic response of a steel arch bridge subjected to near fault ground motions. Earthquake Engineering and Engineering Vibration, Vol. 6, Issue 3, 2007, p. 245-257.
-
Wang R. L., Xu L. Earthquake response analysis with travelling-wave for a long-span steel truss-arch railway bridge. Advances in Structural Engineering, Vol. 18, Issue 8, 2013, p. 1365-1370.
-
Ma J., Li Y. Analysis of travelling wave effect on half-through CFST arch bridge by large mass method. Key Engineering Materials, Vol. 540, 2013, p. 21-28.
-
Wei B., Xia Y., Liu W. A. Lateral vibration analysis of continuous bridges utilizing equal displacement rule. Latin American Journal of Solids and Structures, Vol. 11, Issue 1, 2014, p. 75-91.
-
Guo W., Yu Z. W., Liu G. H., Guo Z. Possible existing seismic analysis errors of long span structures and bridges while utilizing multi-point earthquake calculation models. Bulletin of Earthquake Engineering, Vol. 11, Issue 5, 2013, p. 1683-1710.
-
Guo W., Yu Z. W., Guo Z. An efficient and accurate method for calculating stochastic seismic response of non-proportionally damped structure. Journal of Structural Engineering, ASCE, Vol. 3, 2013, p. 472-477.
About this article
This research is jointly supported by the National Natural Science Foundations of China under Grant No. 51178471, 51322808, 51308549 and 51378504, the Natural Science Foundations of Hunan Province under Grant No. 2015JJ3159, the Ministry of Railways of China (Project No. 2009D04-A), the Program for Changjiang Scholars and Innovative Research Team in University (PCSIRT) (Grant No. IRT1296) and the Scientific Research and Development Program of China Railway Corporation under Grant No. 2013G002-A. The above support is greatly appreciated.
