Composite state variable based nonlinear backstepping design for the underactuated TORA system

1. Introduction

The TORA is composed of a non-actuated translational oscillators and an actuated pendulum so that it has been seen as a classical underactuated mechanical system. It was firstly developed as a simplified model for a dual spin spacecraft [1]. The TORA system has been a research focus with two reasons. One research motivation is the possible use to suppress the translational vibration with a rotational actuation and another is an independent interest to control the TORA as a benchmark problem to design or validate a nonlinear control system or an underactuated control system.

The control problems on TORA have a considerable amount of attention from the all world researchers. There are two focuses on the methods to design a controller, i.e. intelligent design methods and nonlinear design methods. Among the intelligent design methods, some fuzzy based control methods are proposed. The self-tuning fuzzy sliding mode control methods are designed [2, 3] but there are some fuzzy rules and parameters to be preset. A decoupled method is designed to divide the system into two subsystems [4] and two fuzzy controllers corresponding to the subsystems are designed to stabilize the TORA system. However, the fuzzy controllers must be predesigned, and stability cannot be guaranteed. Moreover, some neural network based controllers are proposed. An adaptive neural network controller with SPSA Algorithm is designed [5]. In the literature [6], a method was proposed that is based on system approximation using $n$ neural network. However, a time-consuming learning process is needed and the disturbance rejection cannot be considered. Among the nonlinear design methods, the energy-based design [7-9], the recursive design [10, 11] and sliding mode based design [12], the design processes and the obtained controllers are relatively cumbersome. A comparison study of nonlinear control techniques for the TORA is performed [7]. The energy-based hybrid, entropy-based hybrid, and sliding mode control techniques are experimentally validated and compared on the example of the RTAC testbed. The experimental results indicate that the energy- and entropy-based hybrid controllers use less control effort than the sliding mode controller while stabilizing the zero equilibrium state in less time.

The backstepping design provides a systematic framework and recursive design methodology for nonlinear control [13]. The design procedure treats the state variables as virtual control inputs to design the virtual controllers step by step, and illustrates the stability via the Lyapunov stability theorem. However, a nonlinear feedback cascade model is needed in the traditional backstepping design process and the obtained controllers are relatively cumbersome. In this paper, we propose a backsteppping process that is not based on a nonlinear feedback cascade model but begins from a predefined CSV, and a simple control is expected.

This paper is organized as follows. The TORA system is transformed into a nonlinear system through a collocated partial feedback linearization. Then a nonlinear recursive design method is adopted and a CSV is defined to start the recursive process. The design procedure treats the some state variables as virtual control inputs to design the virtual controllers step by step, and the stability is studied via a stability theorem.

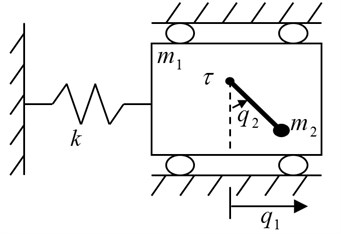
2. The TORA system model

The TORA is shown schematically in Fig. 1. The oscillator consists of a cart of mass $m_1$ connected to a fixed wall by a linear spring of stiffness $k$. The cart is constrained to have one-dimensional travel and its position is $q_1$. The rotational actuator with the output torque is attached to the cart and it has a pendulum with the equivalent mass $m_2$, the rotate radius $r$, the moment of inertia $I$ and the rotate angle $q_2$. Since the rotating torque can not drive the cart directly, it is a benchmark example of the underactuated mechanical system, which has one control input $\tau$ and two configuration variables ($q_1\text{,}$$q_2$), and its Euler-Lagrange equations of motion can be obtained as:

Fig. 1TORA system configuration

Through the following collocated partial feedback linearization [14]:

The dynamics can be reduced to:

3. The nonlinear controller design through backstepping

The controller is designed with the recursive technology and the design process is:

Step 1.

A composite state variable for the nonlinear underactuated TORA system is defined as:

where, $k_1$, $k_2$ and $k_3$ are some positive constants for the system stability to be proved. The derivative of the CSV can be obtained:

According to Eq. (1), Eq. (5) yields:

The $k_2{\dot{q}}_2$ is looked as the virtual input to control the above equation and define a reference trajectory ${\dot{q}}_{2r}$ for ${\dot{q}}_2$ to follow as:

where $b_1$ is a design constant, it leads to an error $e_1$ defined as:

i.e.:

Its derivative is:

According to Eq. (2), Eq. (8) yields:

Consider a scalar positive definite Lyapunov function given by:

Using Eq. (7) and (9), the time derivative $\dot{V}$ is given by:

Step 2.

In step 1, the time derivative of the Lyapunov function $V$ is obtained in Eq. (11). We note that the variable $u$ enters the right hand side of Eq. (11).

In order to make the $\dot{V}$ be negative definite, we can make the following equation hold:

Such that:

Therefore, the control law can be obtained from Eq. (12) as:

Since the system parameters $m_1$, $m_2$ and $r$ are known and $\mathrm{c}\mathrm{o}\mathrm{s}{q}_2\in \text{[-1,}\text{1]}$, the choices of $k_1$ and $k_2$ can make Eq. (14) away from the singularity.

Theorem 1. The TORA system described by Eq. (1) is asymptotically stable to its equilibrium point $(q_1,{\dot{q}}_1,q_2,{\dot{q}}_2)=(\mathrm{0,0},\mathrm{0,0})$under the control input Eq. (2) with Eq. (14) and positive constants $k_1$, $k_2$, $k_3$, $b_1$, $b_2$.

Proof:

The backstepping design process has proved: the time derivative $\dot{V}$ of the chosen positive definite Lyapunov function $V$ is negative definite.

Integrating both sides of Eq. (13) yields:

Then:

We find that:

Therefore it can be obtained that $x_1\in L_{\mathrm{\infty }}$ and $e_1\in L_{\mathrm{\infty }}\text{,}$ i.e. $\mathrm{s}\mathrm{u}\mathrm{p}\left|x_1\right|={‖x_1‖}_{\mathrm{\infty }}<\mathrm{\infty }\text{,}$$\mathrm{s}\mathrm{u}\mathrm{p}\left|e_1\right|={‖e_1‖}_{\mathrm{\infty }}<\mathrm{\infty }$.

At the same time, from Eq. (13):

It is obvious that ${\dot{x}}_1\in L_{\mathrm{\infty }}$ and ${\dot{e}}_1\in L_{\mathrm{\infty }}$, i.e. $\mathrm{s}\mathrm{u}\mathrm{p}\left|{\dot{x}}_1\right|={‖{\dot{x}}_1‖}_{\mathrm{\infty }}<\mathrm{\infty }$, $\mathrm{s}\mathrm{u}\mathrm{p}\left|{\dot{e}}_1\right|={‖{\dot{e}}_1‖}_{\mathrm{\infty }}<\mathrm{\infty }$.

Now let:

Thus:

From our research result (Theorem 1 in [15]), it can be known that $s_1\in L_2$, $s_2\in L_2$ and $s_1\in L_{\mathrm{\infty }}$, ${\dot{s}}_1\in L_{\mathrm{\infty }}$, $s_2\in L_{\mathrm{\infty }}$, ${\dot{s}}_2\in L_{\mathrm{\infty }}$. According to Barbalat’s lemma, $\underset{t\to \mathrm{\infty }}{\mathrm{l}\mathrm{i}\mathrm{m}}{s}_1=0$, $\underset{t\to \mathrm{\infty }}{\mathrm{l}\mathrm{i}\mathrm{m}}{s}_2=0$, i.e. when $t\to \mathrm{\infty }$:

For Eq. (15), a positive definite Lyapunov function $V_1={q_1}^2/2$ is selected and ${\dot{V}}_1=q_1{\dot{q}}_1=-k_3(m_1+m_2){{\dot{q}}_1}^2/k_1$ is negative definite. For Eq. (16), a positive definite Lyapunov function $V_2={q_2}^2/2$ is selected and ${\dot{V}}_2=q_2{\dot{q}}_2=-k_3{m}_{2}r\mathrm{c}\mathrm{o}\mathrm{s}{q}_2{\dot{q}}_2^2/k_2$is negative definite when $q_2\in (-\pi /2,\pi /2)$. Therefore, the TORA system is asymptotically stable to the equilibrium point $(q_1,{\dot{q}}_1,q_2,{\dot{q}}_2)=\text{(0,}\text{0,}\text{0,}\text{0)}$.

Remark 1. As we know, a nonlinear feedback cascade model is needed in the traditional backstepping design process. The proposed design do not need a nonlinear feedback cascade model and it begins from a predefined CSV and treats some state variables as virtual control inputs to design the nonlinear controllers step by step. Therefore, it may be a choice to realize a backstepping design for those systems that can not be transformed into a nonlinear feedback cascade model.

Remark 2. The TORA is a system that can be transformed into a nonlinear feedback cascade model and the backstepping design can be realized [16]. However, the design process and the obtained controller are more cumbersome because the design process is composed of a second-order system design and a first-order system design.

Remark 3. From the process to prove the Theorem 1, it can be seen that the Eq. (15) is convergent only when $k_1$ and $k_3$ have same sign and the Eq. (16) is convergent only when $k_2$ and $k_3$ have same sign, i.e. only when $k_1$, $k_2$ and $k_3$ have same sign, the system is stable. Therefore, some positive constants are chosen for $k_1$, $k_2$ and $k_3$ in Eq. (4).

4. Simulation studies

In order to test the proposed nonlinear control algorithm, the following system parameters [13] are used: $m_1=\text{10}$, $m_2=\text{1}$, $k=\text{5}$, $r=\text{1}$, $I=\text{1}$. The parameters of the nonlinear controller are chosen as $k_1=\text{1}$, $k_2=\text{3}$, $k_3=\text{3}$, $b_1=\text{5}$, $b_2=\text{5}$. The simulation results are shown in Fig. 2 and Fig. 3.

The simulation results in Fig. 2 are obtained under the initial state $\left(q_1,{\dot{q}}_1,q_2,{\dot{q}}_2\right)=\text{(0.1,}\text{0,}\text{0,}\text{0)}$ and the simulation results in Fig. 3 are obtained under the initial state $\left(q_1,{\dot{q}}_1,q_2,{\dot{q}}_2\right)=\text{(0,}\text{0,}\text{18}\text{0}\text{°,}\text{0)}$. It can be seen form the simulation results and many other simulations that the TORA system is asymptotically stable under any initial states with the proposed control algorithm. At the same time, it is shown that it is possible to suppress the translational vibration with a rotational actuation. On the other hand, the control performance can be improved through adjusting the parameters of the proposed controller. Lots of simulation experiments show that the parameters $k_1$, $k_2$ respectively correspond to the system states $q_1$, $q_2$, therefore it is easy to adjust the parameters for a improved system performance. Moreover, compared with the traditional backstepping design [16], it can be seen that the control performance of the proposed method is improved from the simulation results in [16] with the same system parameters or more difficult-to-control initial state. If only the simulation or experimental results are compared with the other control algorithms [2-12], a shorter stabilization time, a better states response and a lower number of oscillations are realized. Therefore, the proposed controller is simpler and more efficient.

Fig. 2Simulation results under system initial state q1,q˙1,q2,q˙2=(0.1, 0, 0, 0)

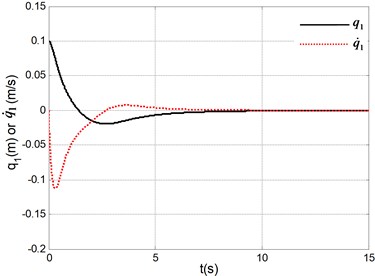
a) Position and velocity of the cart

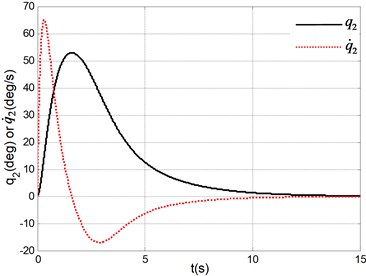
b) Angle and angle velocity of the pendulum

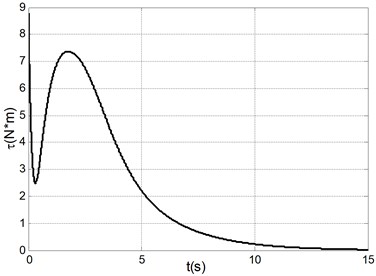
c) Control torque

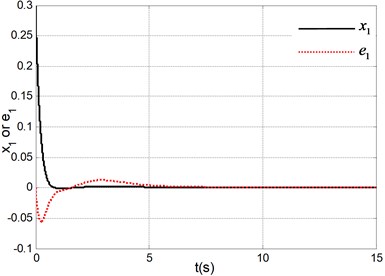
d) Responses of CSV $x_1$ and error $e_1$

Fig. 3Simulation results under system initial state q1,q˙1,q2,q˙2=(0, 0, 180°, 0)

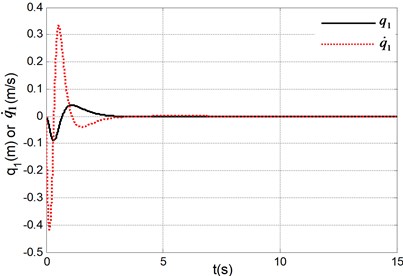
a) Position and velocity of the cart

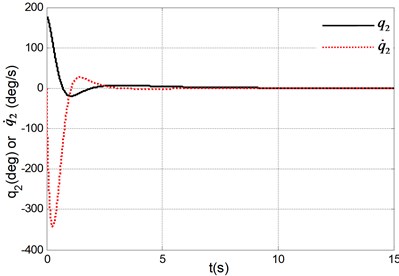
b) Angle and angle velocity of the pendulum

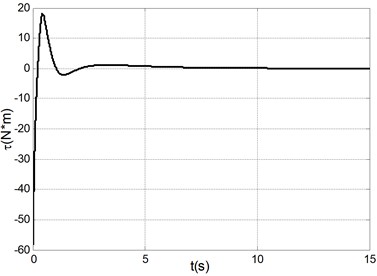
c) Control torque

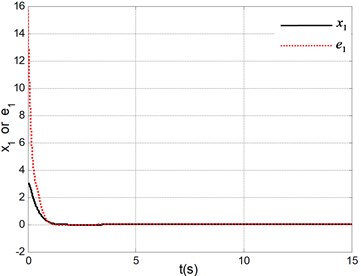
d) Responses of CSV $x_1$ and error $e_1$

5. Conclusions

Using a collocated partial feedback linearization, the underactuated TORA is transformed to a nonlinear system that is used in the recursive process. A CSV is defined and a nonlinear control algorithm is proposed with the recursive technology. The design procedure treats the state variables as virtual control inputs to design the virtual controllers step by step, and the system stability is studied via a stability theorem.