Numerical simulation and experimental research of flow-induced noise for centrifugal pumps

3.1. Basic theory and solving strategy

As the fluid in centrifugal pumps is water in this paper and its temperature change is neglected [9, 10], the fluid can be computed as an incompressible and thermal insulation fluid. During the computation, the energy equation can be negligible. The control and momentum equations can be expressed as follows [11]:

wherein, $\rho$ is the fluid density, $u$ and $p$ are the speed and pressure, respectively. $t$ is the time, $\mu$ and $S$ are the dynamic viscosity and source term, respectively.

Fig. 1Mesh model of the computational domain for centrifugal pumps

a) Mesh model of centrifugal pumps

b) Local mesh of the impeller blade wall

The finite volume method is used to conduct the discreteness of Eq. (1), and the fully implicit multi-mesh coupled solution technology is also applied to solve it. Wherein, the discreteness of the time term adopts the second-order implicit scheme, the diffusion term and pressure term are dispersed by the central difference scheme, and the second-order upwind scheme is used for the convection term. In order to fully capture the pressure fluctuation changes on the upstream and downstream of the impeller, the physical time step of the unsteadily computation is set as 1/10 of an angle rotated by the impeller. Therefore, the unsteadily computation physical step is 0.00035 s. In a physical time step, the absolute residuals of the equation variable are controlled less than 10^-4, and then the next time step is computed. Before the unsteady computation, the steady computation is made firstly, and then the result of the steady computation is taken as the initial conditions of the unsteady computation. Finally, the unsteady computation is conducted.

3.2. Computation of boundary conditions

The inlet is set the pressure boundary condition, the outlet is set the boundary condition of the mass flow, the rotary area is set the rotation speed of 2900 r/min, and others adopt the defaulted solid wall boundary condition. Due to the limited computing resources, the rated operating conditions are adopted in this paper for analysis and computation.

3.3. Arrangement of the computational monitoring points

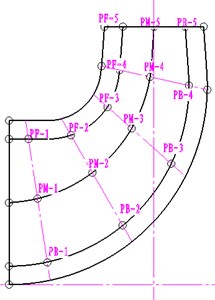
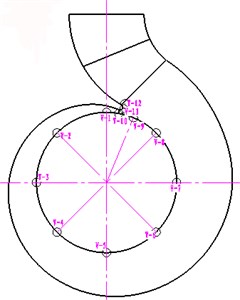
In order to specifically analyze the influence of the dynamic and static interference on the upstream and downstream of the impeller, the monitoring points are arranged at the front and back cover as well as the middle position near the operation face of the impeller blade and its reverse face in this paper (PF is the monitoring point near the front cover, PM is the monitoring point in the middle position, and PB is the monitoring point near the back cover). Meanwhile, the relevant monitoring points are arranged at the dynamic and static interface in the peripheral direction of the volute. In addition, three monitoring points are also placed at the tongue, as shown in Fig. 2.

3.4. Experimental verification

To verify the accuracy of the numerical computation, the experimental system of the exterior performances for centrifugal pumps is built. It is composed by the water circulation system and data collection system. The necessary environment for the operation of centrifugal pumps is provided by the water circulation system. By means of the sensor, the data collection system transfers various physical signals existed in the operation of the centrifugal pump under different conditions into the corresponding electrical signals. And after a series of processes, they are converted into the directly identified data. The experimental system is shown in Fig. 3.

Fig. 2Monitoring points of the pressure fluctuation inside the impeller and the interface of the dynamic and static volutes

a)

b)

Fig. 3Experimental system of the external performances for centrifugal pumps

Fig. 4Comparison of the exterior performances between experiment and simulation

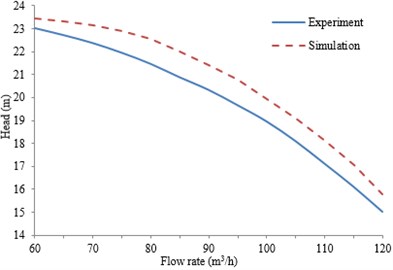
a) Head change curve with flow rate

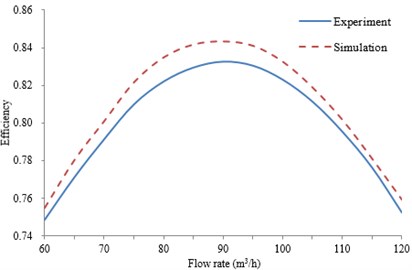
b) Efficiency change curve with flow rate

The discharge valve is adjusted step by step according the flow rate increasing from 60 m³/h to 120 m³/h, which is the high pressure safety injection process. When the pump operated at $Q=$60 m³/h stably, the discharge valve is adjusted with a uniform rate to increase the flow rate and it will be stopped until the flow rate increased to 120 m³/h approximately. The variable flow rate during the adjustment process is measured. The computed exterior performances (head $H$ and efficiency $\eta$) of centrifugal pumps are compared with the experimental values, as shown in Fig. 4. As can be seen from Fig. 4, the maximum error of the computational head is 4.8 %, and the maximum error of the computational efficiency is 4.3 %. They are within the acceptable difference between the experimental and simulated results because of the mechanical losses, and overall good agreement between the simulation results and the experimental results can be observed. So the numerical simulation method can be considered reliable in this paper, which can be used for the subsequent researches.

4.1. Pressure fluctuation analysis inside the impeller

To research the pressure fluctuation inside the impeller, the pressure fluctuations of 36 monitoring points arranged inside the impeller are computed and collected. Data within $t=$ 0.2-0.24 s is conducted FFT analysis, so as to obtain the pressure fluctuation amplitude changes of each monitoring point with the frequency, as shown in Fig. 5 and Fig. 7.

Fig. 5Pressure fluctuation near the operation face of the impeller

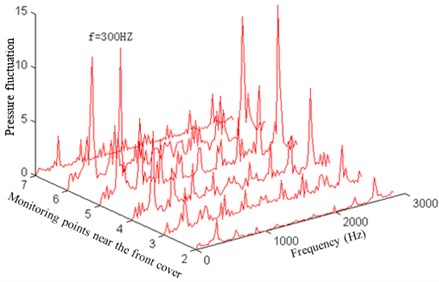
a) Pressure fluctuation near the front cover of the operation face

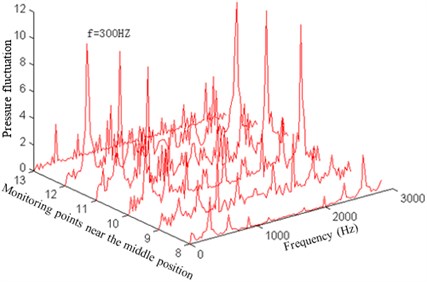
b) Pressure fluctuation near the middle position of the operation face

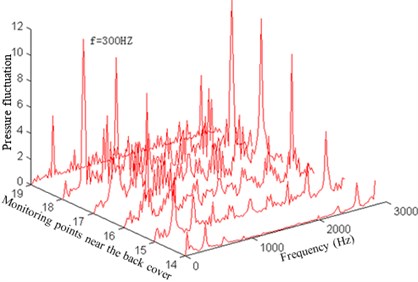
c) Pressure fluctuation near the back cover of the operation face

As shown in Fig. 6(a), (b) and (c), the flow velocity distribution of passage 5 and 6 in the centrifugal pump is calculated under 0.7$Q$, 1.0$Q$, and 1.3$Q$ flow rate. As can be seen from the figures, the flow velocity is significantly increased at the impellers with the increase of flow rate, which is also consistent with the actual situation. It can be clearly seen the flow trajectories and velocity distribution in the centrifugal pump from the 3D geometry in Fig. 6(d).

Fig. 6Flow velocity distribution in the centrifugal pump

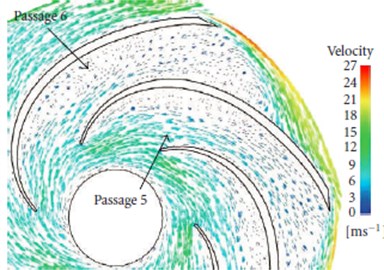
a) 0.7$Q$

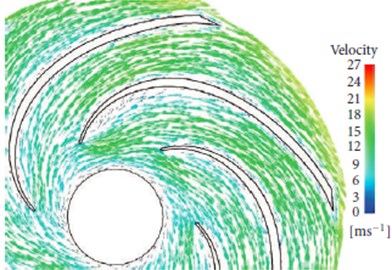
b) 1.0$Q$

c) 1.3$Q$

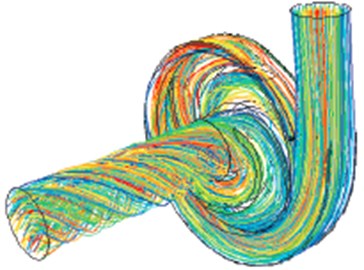
d) 3 D distribution

Fig. 7Pressure fluctuation amplitude of the main frequency on the operation face spreads from the inlet to the outlet inside the impeller flow channel

As can be seen from Fig. 5, the pressure fluctuation peaks of the impeller operation face which is close to the front cover and middle position as well as back cover are mainly in the rotation frequency, blade frequency, double blade frequency, triple blade frequency and quadruple blade frequency. But in the impeller outlet, some low-frequency components (1/2 rotation frequency) and high-frequency components increase, making the pressure fluctuation complicated and main frequency weakened. This result is mainly caused by the mutual interference of fluids between the impeller and volute.

As can be seen from Fig. 7, the pressure fluctuation amplitude at the main frequency increases firstly and then decreases from the impeller inlet to the outlet at the impeller operation face. The larger amplitude is appeared at 0.45 to 0.80 times of the blade length.

As can be seen from Fig. 8, the pressure fluctuation peaks on the reverse face of the impeller are similarly to those of the operation face.

Fig. 8Pressure fluctuation near the reverse face of the impeller

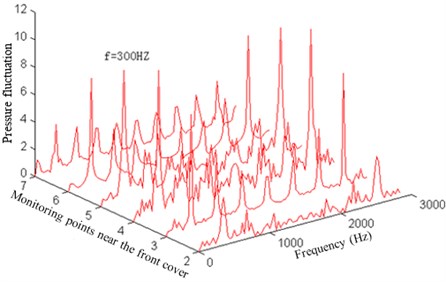
a) Pressure fluctuation near the front cover of the reverse face

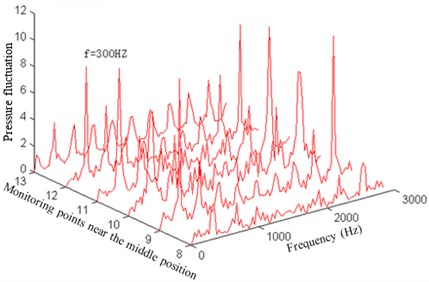
b) Pressure fluctuation near the middle position of the reverse face

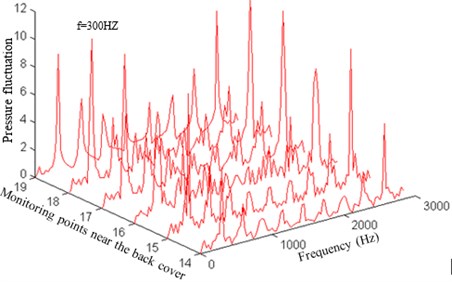
c) Pressure fluctuation near the back cover of the reverse face

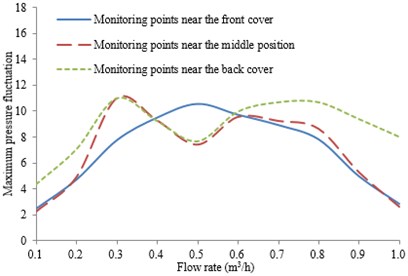
In addition, it can be seen from Fig. 9 that the pressure fluctuation amplitude at the main frequency increases firstly and then decreases near the front cover. In the middle position and back cover, its amplitude increases and then decreases. However, it increases and decreases again in the outlet. In terms of the pressure fluctuation spreading law at the main frequency inside the impeller flow channel, the pressure fluctuation near the operation face is greater than that near the reverse face. On the operation face, the maximum pressure fluctuation amplitude is in the front cover of the impeller flow channel, while on the reserve face, it occurs in the middle position of the impeller inlet.

Fig. 9Pressure fluctuation amplitude of the main frequency on the reverse face spreads from the inlet to the outlet inside the impeller flow channel

4.2. Pressure fluctuation analysis inside the volute

The pressure fluctuation inside the impeller flow channel is analyzed in detail as the above. However, the volute is one of the main components in a centrifugal pump. Therefore, the pressure fluctuation distribution inside the volute is also necessary to be researched. The pressure fluctuation of the monitoring points in Fig. 2 is also extracted as Fig. 10.

Fig. 10Pressure fluctuation in the peripheral direction of the volute

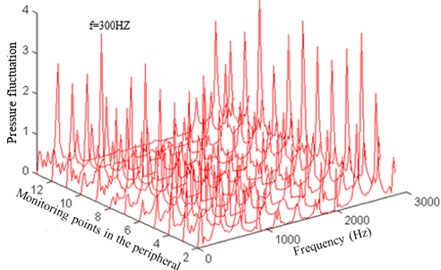
Fig. 11Pressure fluctuation amplitude of the main frequency in the peripheral direction of the volute spreads along with the helix direction

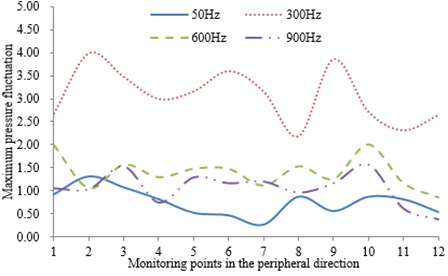
As can be seen from Fig. 10, the higher pressure fluctuation peaks in the peripheral direction of the volute mainly appears in the rotation frequency, blade frequency, double blade frequency and triple blade frequency.

In addition, as can be seen from Fig. 11, the pressure fluctuation amplitude which is change from large to small are located at 300 Hz, 600 Hz, 900 Hz and 50 Hz. Wherein, the greater pressure fluctuation amplitudes at each frequency are mainly in 1, 9, 10 points which are close to the tongue. But compared to the pressure fluctuation inside the impeller, the pressure fluctuation amplitude in the peripheral direction of the volute is smaller. This is mainly due to the quite stable expulsion effect of the volute spiral changes on the liquid and small pressure fluctuation.

5.1. Computation of the structural modal

Centrifugal pumps are a rather complex structure obtained by casting and machining, as shown in Fig. 12(a). The finite element model is prepared for the interaction between the fluid and structure, and the local characteristics and stress condition of the structure are not necessary to be considered. Therefore, during building the model, the hole, boss, chamfering and other detailed structures are ignored and only some important structures are considered, as shown in Fig. 12(b).

Fig. 12Entity and simplified model of the volute

a) Entity

b) Simplified model

The material used in the simulation is steel, with the properties elastic module $E=$211 GPa, the density $\rho =\mathrm{}$7850 kg/m³, the Poisson ratio $\mu =$ 0.29. The excitation force is set as the boundary condition. The constraints are imposed as follows: the nodes of the foundation bolt hole are completed fixed, with $u_x=u_y=u_z=\text{0}$. The displacement of nodes on the bearing holes is $u_x=u_y=u_z=\text{0}$. $u_z=\text{0}$ on the inlet flanges, $u_x=\text{0}$ on the outlet flanges. The boundary set is shown in Fig. 14. The precision and scale of the computation are directly affected by the quantity of the mesh, as shown in Table 3.

As can be seen from Table 3, with the decrease of the mesh density, the number of meshes and node is also decreased gradually, and the natural frequency is reduced too. When the mesh size is less than 10 mm, the maximum relative error of the natural frequency is less than 1 %. Therefore, the modal result computed at the mesh size of 10 mm is adopted for the subsequent analysis.

5.2. Sound field on the surface of the centrifugal pump

The vibration source of the flow-induced noise in the centrifugal pump is mainly the pressure pulsation which is generated from the static and dynamic interference within the pump. As such pulsation acts on the volute and the internal surface of pump cover, the excitation force is generated and transferred to the outer surface through the pump cover structure, and then the vibration on the outer surface of the pump cover is caused, which will generate coupling with the air, thus making noise.

The calculation process of this coupling is shown in Fig. 13. 1) The internally unsteady flow is solved by means of large eddy simulation, in order to obtain the time domain fluctuation of pressures on interface between structure and fluid. 2) The vibration displacement response of the pump cover structure is simulated under the excitation of pressure fluctuation. 3) The natural modes of the cover structure are solved. 4) The vibration displacement on the outer surface of the cover structure is taken as the boundary condition, and FEM/BEM coupling method is applied to solve the flow-induced noise based on the structural modes.

Fig. 13Calculation process of coupling for the centrifugal pump

Fig. 14Finite element mesh

Fig. 15Mesh on the surface

The outer surface of the structure was extracted and meshed as the acoustic model used in the BEM calculation, as shown in Fig. 15. The acoustical mesh consists of 14706 elements and 13757 nodes. As the maximum valid frequency of the model investigated in the study was 4366 Hz. According to the reference [12]. The normal velocity distribution on the outer surface nodes of the structure was transferred to the surface nodes of the acoustic model, which was set as the boundary condition of the volute acoustic simulation.

The sound field is computed by using the boundary element method. Assuming the acoustic waves at the inlet and outlet are plane waves, and the property at the inlet and outlet is set as the sound absorption. If the coupling is considered, the structural modal result is required to be imported. And the modal damping of the volute is set as 0.01. When the mapping between the acoustic boundary element mesh and structural finite element mesh is only completed, the coupling response solution can be conducted. The computational result from the coupled and uncoupled acoustic boundary element is shown in Table 4, and the corresponding distribution of the sound pressure level (SPL) is shown as Fig. 16.

Fig. 16SPL distribution of the volute at 300 Hz

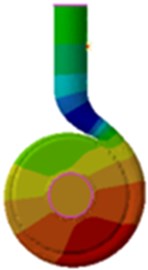
a) Uncoupling

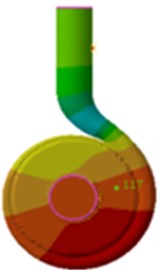
b) Coupling

From Fig. 16 and Table 4, it is found that SPL distribution is similar in both situations, and the maximum values are all appeared in the inlet and outlet. The position of the minimum value is also close to the inlet and outlet, and the dipole characteristic of the sound field distribution remains unchanged. In both conditions, SPL decreases along with the increase of the flow rate. According to Table 4, the maximum SPL differs little under both conditions, while the minimum values differs much, reaching up to 10.6 dB. At double blade frequency, the influence of the acoustic coupling on the distribution of the sound field is most obvious. The minimum values of each condition differed about 10 dB because the first-order natural frequency of the centrifugal pump volute is about 602 Hz, which is close to double blade frequency. According to the above analysis, the acoustic coupling can’t be neglected to solve the flow- induced noise of centrifugal pumps.

The coupled boundary element method is applied to compute the sound field distribution of the sound source term for the volute pressure fluctuation. The outlet $B_1$ (26, 225, 0) is set to calculate SPL. The flow-induced noise of centrifugal pumps is very complicated, so it is necessary to verify the reliability by means of experiment. The measurement of the far-field noises in the centrifugal pump is always interfered by the motor noises, pipe noises and background noises, thus causing some difficulties to obtain the accurate results. In order to verify the reliability of the numerical results, the internal noises of the centrifugal pump are tested and the corresponding signal is measured by a hydrophone. The hydrophone type is ST70. The hydrophone is installed in the pipe wall horizontally. And the sensor probe is in the flush status with the wall surface around the measurement point, which measures the flow noise within the pipe directly. The hydrophone is arranged in the outlet location of the centrifugal pump. The experimental equipment is shown in Fig. 3. The test results are then compared with the numerical results, as shown in Fig. 17. It can be seen that the experimental result is close to the numerical result no matter in peaks or other frequencies. Therefore, the numerical simulation model is reliable and can be used for the subsequent analysis.

Based on the verified model, the inlet $B_2$ (33, 0, 212) is also set to calculate SPL and compared with that of the inlet, as shown in Fig. 18.

Fig. 17Comparison of noises at the outlet between experiment and simulation

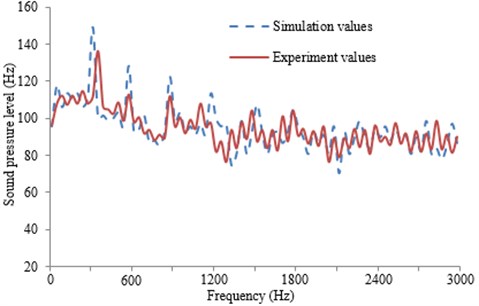
Fig. 18Response curve of the SPL frequency domain

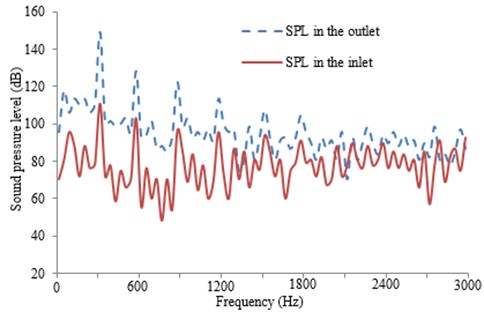
As can be seen from Fig. 18, during computing the sound field, the computational result is a broadband when the pressure fluctuation of the volute is regarded as the dipole source. At low frequency, SPL at the outlet $B_1$ is obvious larger than that of the inlet $B_2$, indicating that the influence of the volute is larger on the sound field when it is compared with that of the inlet. There are peaks at the blade frequency and double blade frequency, indicating that the interference between the blade and tongue is the main reason for the flow-induced noise of centrifugal pumps.

5.3. Radiation noises at the far-field for the centrifugal pump

In the above analysis, only noise on the surface of the internal structure for the volute is researched. The radiation noise of the centrifugal pump is also very important and should be researched.

BEM method is applied to calculate the radiation noise at the far acoustical field of the centrifugal pump. The propagation medium is air, which density is 1.225 kg/m³, and the corresponding propagation speed is 340 m/s. A spherical field-point mesh is created at 1.5 m away from the geometric center of the centrifugal pump, in order to observe the sound pressure distribution. The radiation sound pressure of the centrifugal pump cover under different impeller outlet width is shown as Fig. 19. It can be seen from the figure that with the increase of the impeller outlet width $W$, the radiation sound pressure of the centrifugal pump is increased significantly. Therefore, the radiation noise at the far acoustical field is relatively small when the impeller outlet width is 8 mm.

Fig. 19The radiation noises of the centrifugal pump cover

a)$W_1=$ 8 mm

b)$W_2=$ 10 mm

c)$W_3=$12 mm

d)$W_4=$14 mm

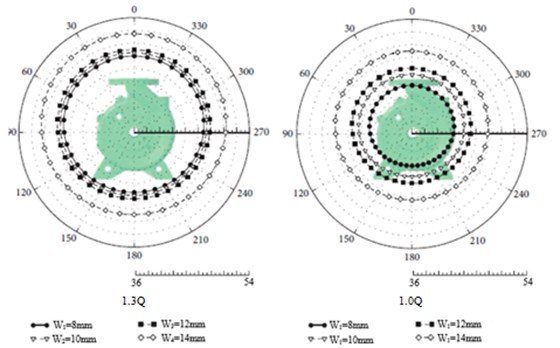
There is an obvious direction in the propagation of sound. There are different directions for different points which are relative to the sound source position. As a result, their noise spectrums are also different. To obtain the circumferential distribution of the centrifugal pump SPL, 36 monitoring points which are 1500 mm away from the impeller center are set up on the external surface of the pump cover, and the angle is 10° between the adjacent points. Finally, the radiation noise of the centrifugal pump at the far acoustical field under different conditions is obtained, as shown in Fig. 20.

As can be seen from Fig. 20, SPL is not significantly changed when the impeller outlet width is increased from 8 mm to 12 mm, while SPL has an obvious change when the width is increased from 12 mm to 14 mm. Therefore, the increase range of SPL is also increasing gradually under all conditions with the increase of the impeller outlet width. On one hand, the increases of the impeller outlet width are conducive to eliminating swirls of the secondary flow on the volute section, but reflux will be caused by the excessive impeller outlet width. As a result, the static and dynamic interference between the impeller and volute will be strengthened. On the other hand, there is an obvious impact of the impeller outlet width on the jet flow wake of the impeller outlet, and the area of the wake is also enlarged with the increasing outlet width [13]. Therefore, with the increase of the impeller outlet width, the pressure fluctuation generated by the static and dynamic interference within the pump is strengthened, and the fluid excitation and vibration noise will be also strengthened. Therefore, the impeller outlet width must be designed well. Otherwise, greater radiation noise will be generated in the far field.

Fig. 20Directivity distribution of the radiation noises for the centrifugal pump