Analysis of the influence of braking control laws on gear walk

2.1. Landing gear structural modeling

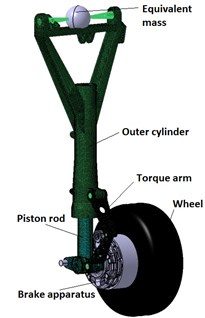
The rigid-flexible coupling dynamic model of the half-axle main landing gear shown in Figure1 is built in LMS Virtual.Lab Motion based on some data of some type of airplane. The flexibility of the piston rod, the outer cylinder and the torque arm is considered in the model.

Fig. 1Rigid-flexible coupling multi-body model of the half-axle main landing gear. The piston rod, the outer cylinder and the torque arm are flexible bodies; the equivalent mass, the wheel axle and the brake apparatus are rigid bodies. The tire model is based on Pacejka tire model, see Section 2.2

2.2. Tire model

The tire model used in this study is based on classic Pacejka Magic-Formula tire model [15], the magic formula is:

where $Y\left(x\right)$can either be lateral force, aligning torque or longitudinal force, the independent variable $x$ can be sideslip angle or slip rate, the coefficients $B$, $C$, $D$ can be determined by vertical load and camber angle.

The tire deflection $\delta$ is calculated by [17]:

where $\delta$ is the deflection caused by the tire vertical force, $F$ is the tire vertical force, $p_0$ is the actual tire inflation pressure, $p_t$ is the rated tire inflation pressure, $W$ is the tire sectional width, and $D$ is the tire diameter, respectively.

The corresponding tire internal pressure $p$ is given by [18]:

Slip rate is a parameter used to measure the brake level of a tire. It is defined as the amount of the tire skidding relative to the ground. The slip rate $\sigma$ is defined as:

where $v_x$ is the forward taxiing speed, $v_w$ is the linear velocity of the tire.

During the braking process, the friction coefficient [16] between the tire and the ground is computed according to the slip rate$\sigma$, namely:

– Dry runway:

– Wet runway:

– Icy runway:

The rotation of the wheel is caused by the friction torque $M_f$ and by the braking torque $M_b$:

where $\omega$ and $\dot{\omega }$ are the angular velocity and the angular acceleration, $J_r$ is the rotational inertia of a wheel, $R_g$ is the rolling radius, respectively.

The friction torque $M_f$ can be calculated by:

where $\mu$ is the friction coefficient between the tire and the ground, $F_1$ is the frictional force between the tire and the ground, and $N$ is the bearing reaction force of the tire.

2.3. Shock absorber model

The shock absorber of the half-axle main landing gear is a single-cavity oleo-pneumatic shock absorber. The buffer axle force consists of air spring force $F_a$, oil damping force $F_h$ and structure restriction force $F_l$ [16]. The expression of the buffer axle force is:

Without regard to the compressibility of hydraulic oil and the change of cavity volume, the air spring force $F_a$ can be calculated by:

where $A_a$ is the cross section area of the air cavity, $P_0$ is the original additive gas pressure, $n$ is the air polytropic exponent, and $P_{atm}$ is the atmospheric pressure.

Assume that the oil hole area of the main oil cylinder cavity remains the same and there exists a side oil hole, then the oil damping force $F_h$ can be computed as:

where ${\rho }_{oil}$ is the oil density, $A_h$ is the effective cross section area of the main oil cavity, $A_d$ is the oil hole area of the main oil cavity, $C_d$ is the contraction coefficient of the main oil cavity, $A_{hs}$ is the effective cross section area of the return oil cavity, $A_n$ is the oil hole area of the return oil cavity, and $C_{ds}$ is the contraction coefficient of the return oil cavity, respectively.

The structure restriction force $F_l$ is given by:

where $k_l$ is the structure restriction stiffness, and $s_{max}$ is the compression stroke of the shock absorber.

2.4. Fundamental dynamic model verification

2.4.1. Comparison of dynamic simulation with experiment results

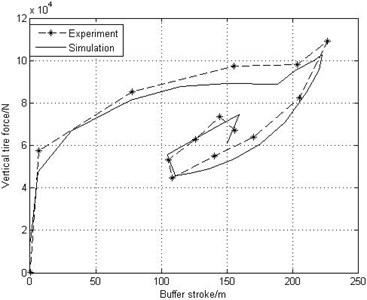
The simulation of the tire static curve, the landing gear drop test and the first order longitudinal mode of the rigid-flexible coupling model is carried out based on the landing gear dynamic model. Simulating results are compared to the corresponding experimental data. The comparisons are shown in Fig. 2, Fig. 3 and Table 1.

Table 1Comparison of simulation and test of the main landing gear first order longitudinal mode

Buffer stroke / mm	0	100	250
Simulation / Hz	78.13	85.24	92.07
Test / Hz	72	79	88
Error / %	8.5	7.9	4.6

From Fig. 2 it is seen that the simulation of the tire static curve agrees well with the experiment results. Comparisons of the drop dynamic figure of the main landing gear drop test shown in Fig. 3 and the main landing gear first order longitudinal mode listed in Table 1 show that the simulation of the drop test is similar to the experiment data and the error of the first order longitudinal mode between the simulation and the experiment results is within 10 %. Therefore, the established rigid-flexible dynamic model is correct and effective.

Fig. 2Tire static curves of simulation and experiment

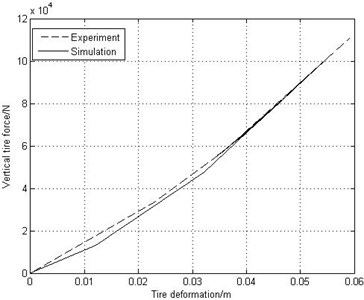
Fig. 3Drop dynamic figure of main landing gear drop test and simulation

2.4.2. Verification of the gear walk dynamic model during landing

When the tire just touches the ground before the braking system starts working, the rotational speed of the wheel accelerates from stationary state to pure rolling state. During this landing process, the fore and aft vibration of the landing gear strut occurs. According to the test data and relevant information in literature [11], at the moment when the tire touches the ground, the peak value of landing gear longitudinal acceleration can reach from ±15 g to ±30 g. Fig. 4 illustrates that the wheel axle longitudinal acceleration is approximately ±20 g, consistent with the test results. Therefore, the brake-induced vibration model is verified and fitted well with the dynamic characteristic of the actual landing gear, thus can be used to investigate the gear walk.

Although the peak value of landing gear longitudinal acceleration reaches 20 g at the moment when the landing gear touches the ground, such a high acceleration of the wheel axle will produce unstable longitudinal vibration during braking process. As a result, a braking system with an appropriate braking torque is necessary to reduce the phenomenon of the gear walk.

Fig. 4Wheel axle acceleration-time diagram after the tire touching the ground

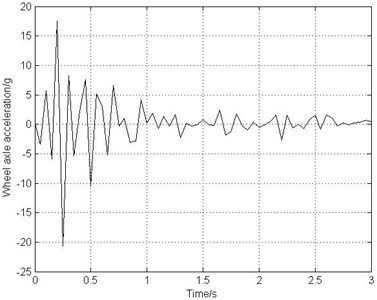
Fig. 5Wheel axle displacement-time diagram after the tire touching the ground

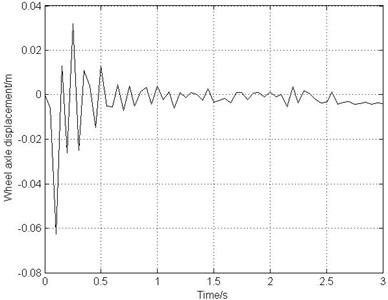
Fig. 5 shows that the initial longitudinal displacement of the wheel axle reaches maximum values ranging from –0.06 m to +0.03 m. Then the amplitude decays rapidly to around zero. After 1 second of landing, the landing gear and the rotating wheel come to a steady state and then the braking system starts to work.

3.1. Deceleration braking control system modeling

The original braking control system of this type of airplane is deceleration braking control. This braking control law is simple to design and easy to take into practice. However, it is of low braking efficiency [17] and would lead to severe gear walk. The deceleration braking control theory is that the braking system detects the forward velocity through the velocity sensor and calculates the deceleration of the airplane, then the braking system outputs braking torque. When the deceleration is lower than 5 m/s², the braking system starts to output braking torque of 10000 N∙m to the rotating wheel, while the deceleration is higher than 5 m/s², the braking system stops working. The expression of the braking control law is given below:

where $M_b$ is the braking torque.

This braking control system model is established in MATLAB/Simulink, is joint-simulated with the dynamic model presented in Section 2 to study the vibration performance of the gear walk.

3.2. Simulation results and discussion

The deceleration braking control system starts to work after 1 second of landing. The landing operating condition is that the runway is dry and smooth. The landing forward velocity is 77 m/s. The equivalent longitudinal stiffness of the landing gear strut is 1.04e6 N/m. The frictional coefficient between the brake disks is 0.25. Fig. 6(a) shows that the airplane can stop completely in 20 s and the airplane brakes with a constant deceleration. However, Fig. 6(b) indicates that the rotating speed of the braking wheel shocks with poor stability and in high frequency. Fig. 6(c) shows that the slip rate fluctuates around 0.05 rather than the optimal value 0.15 so that the frictional coefficient and the frictional force are relatively small, resulting in low braking efficiency. Fig. 6(d) and Fig. 6(e) illustrate that the fluctuating frequency of braking torque is very high which leads to high vibrating frequency of gear walk. As time goes on, the braking torque adjusts more frequently and the phenomenon of brake-induced vibration becomes more serious. Fig. 6(f) shows that the longitudinal acceleration of the wheel axle increases gradually and the amplitude value reaches 20 g. As mentioned previously in Section 2.4.2, the vibration becomes unstable when the longitudinal acceleration reaches 20 g. That will not only shorten the fatigue life of landing gear, but also cause severe accidents.

4.1. Reference speed-speed difference braking control system with PBM (Pressure-Bias-Modulated) control system modeling [16]

4.1.1. PBM reference speed-speed difference braking control law

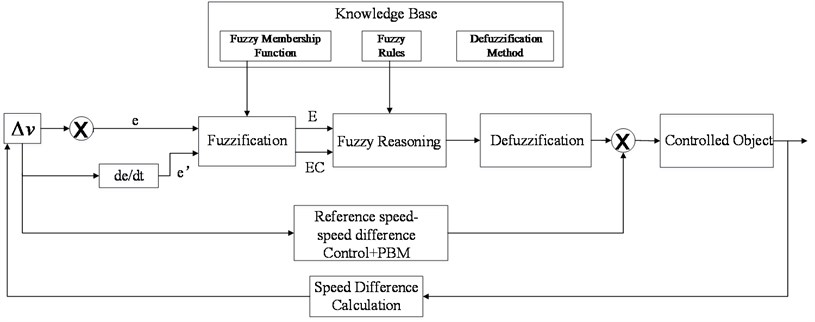
This type of braking control law is similar to the classic PID control. The difference is that in order to obtain better braking performance, the integration coefficient of this controller is variable due to the input. The input of the reference speed-speed difference braking control system with PBM is quasi slip velocity. Slip velocity is the difference between the airplane forward velocity and the linear velocity of the braking wheel. The control system replaces the airplane forward velocity with the reference speed and then the quasi slip velocity can be figured out. This type of control law is of more accurate control and better stability since detecting the actual airplane forward velocity is not necessary. The diagram of this control theory is shown in Fig. 7.

Fig. 6Simulation results of deceleration-rate braking system

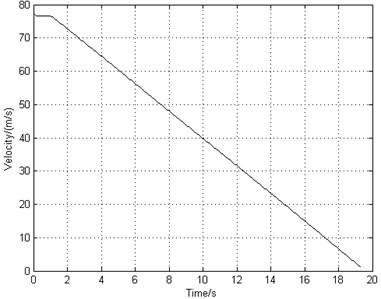
a) Aircraft speed

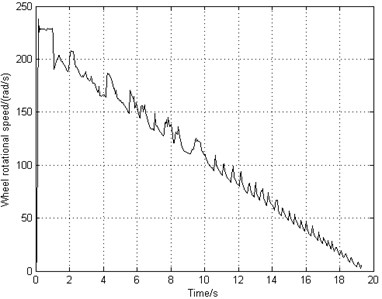
b) Wheel speed

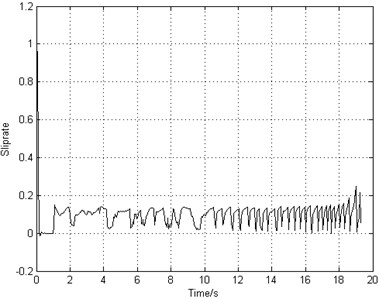
c) Slip rate

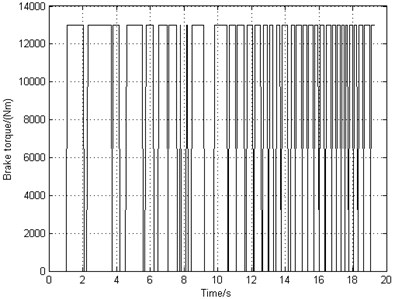
d) Brake torque

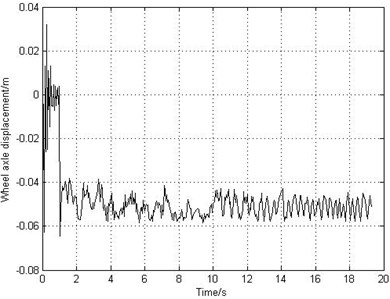
e) Longitudinal displacement of wheel axle

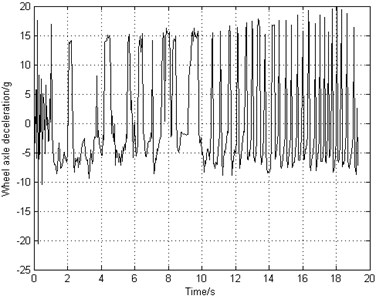
f) Longitudinal acceleration of axle wheel

The reference speed-speed difference braking control box with PBM contains not only the speed input and the reference speed calculation module in the dashed box in Fig. 7, but also the comparator and PBM modules. The control process is that the reference speed is calculated by the reference deceleration and the linear velocity of the braking wheel, then the wheel linear velocity and the reference speed are compared and amplified. The comparator output is the input of PBM module. The desired control effect is to make the wheel linear velocity tend to converge to the reference speed. And the output of this PBM module is the input of the brake apparatus.

Fig. 7Diagram of the reference speed-speed difference braking control theory

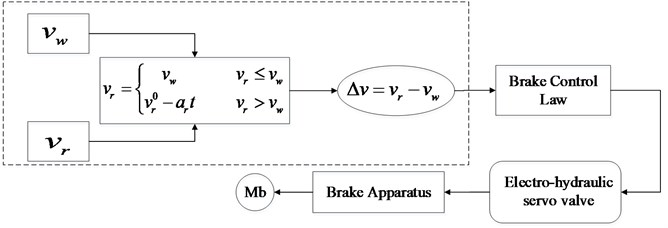
4.1.1.1. Reference speed module

The following control law should be obeyed. If the wheel linear velocity is higher than the reference speed, the reference speed is then equal to the wheel linear velocity, otherwise the reference speed decreases according to a constant reference deceleration. The reference speed is computed by:

14

$v_r=\left\{\begin{array}{c}{v}_w,v_r\le v_w,\\ v_r^0-a_{r}t,v_r>v_{w,}\end{array}\right.$

where $v_r$ is the reference speed, $v_w$ is the wheel linear velocity, $v_r^0$ is the reference speed of the previous instantaneous moment, and $a_r$ is the reference deceleration, respectively.

If the wheel linear velocity is higher than the reference speed, it means that the braking torque is insufficient. Then the reference speed is equal to the wheel linear velocity so that the anti-skid electric current is about zero which enlarges the braking torque to the peak value. On the contrary, the braking torque will decrease to release the excessive brake.

The value of deceleration has great influence on braking system. If the deceleration is too large, the control system would response slowly. If the deceleration is too small, the system would encounter high frequency oscillations.

4.1.1.2. Comparator

The difference between the reference speed and the wheel linear velocity is amplified and output to the next module. The expression is:

15

$∆V_c=K_c\left(v_r-v_w\right),$

where $∆V_c$ is the output voltage of the comparator, $K_c$ is the proportional gain.

4.1.1.3. Proportion and differentiation modules

The proportion module is the proportional cycle amplifying the output of the comparator:

16

$∆V_p=K_p∆V_c,$

where $K_p$ is the proportional coefficient.

The differentiation module is:

17

$∆V_D=K_D\frac{d(∆V_c)}{dt},$

where $K_D$ is the differential coefficient.

4.1.1.4. PBM module

The control theory of PBM is to settle different threshold values and different control parameters according to the input value. If the input, the difference between the reference speed and the wheel linear velocity, is higher than a certain threshold value, it means that the braking torque is too high and a bigger control parameter is needed to reduce the braking torque sharply. If the input value is lower than that threshold value, then a smaller control parameter is needed to decrease the braking torque gently. If the input value is close to zero, another control parameter is needed to increase the braking torque to improve the braking efficiency. The output voltage $V_I$ of PBM module is defined as:

18

$V_I=\left\{\begin{array}{ll}{V}_0^{\text{'}}+\int \left(∆V_c-∆V_{T1}\right)dt,& 0<∆V_c-∆V_{T1}\le ∆V_{T2},\\ V_0^{\text{'}\text{'}}+\int K_{1}dt,& ∆V_c-∆V_{T1}>∆V_{T2},\\ V_0^{\text{'}\text{'}\text{'}}-\iint K_{2}dtdt,& ∆V_c-∆V_{T1}\le 0,\end{array}\right.$

where $V_0^{\text{'}}$, $V_0^{\text{'}\text{'}}$ and $V_0^{\text{'}\text{'}\text{'}}$ are the voltage values of the last instantaneous moment, $∆V_{T1}$ and $∆V_{T2}$ are the threshold values, $K_1$ and $K_2$ are the control parameters.

4.2. Simulation results and discussion

The landing operating condition is the same as the one used in Section 3.2. Fig. 8(a) indicates that the airplane stops in 20 s smoothly, remaining the same braking time comparing to the deceleration brake, while Fig. 8(b) illustrates that the rotating speed of the braking wheel shocks markedly slightly. As can be seen from Fig. 8(c) that the slip rate keeps increasing during the whole taxiing process even though the value ranging from 0.1 to 0.2, the braking efficiency is not high either. Fig. 8(d) show that of the braking torque frequency drops by about 25 % and the torque amplitude fluctuates much more mildly in comparison with the deceleration brake. Fig. 8(e) demonstrates the high vibrating frequency of gear walk resulting from high frequency braking torque and the vibration amplitude growing gradually when braking, but still smaller vibration amplitude and lower frequency comparing to the deceleration brake. Fig. 8(f) shows that after 2 seconds, the longitudinal acceleration of the wheel axle remains under 5 g, acceptable according to the data in reference [11].

5.1. Combined braking control system designing and modeling

To solve the problems of the severe gear walk caused by both the deceleration and only PBM braking control laws, a new braking control law is promoted and designed for this type of airplane. The control law combines reference speed-speed difference braking control with fuzzy control [19] to replace the original deceleration control law on the half-axle landing gear to stop the airplane.

The reference speed-speed difference braking control system is the same as Section 4. Due to the complexity and nonlinearity of braking system, the braking process would be inefficient and the robustness would be weak if there is only the PBM control is used in the braking system. Therefore, adding fuzzy control into the braking system would be necessary and would improve the braking performance. The fuzzy control law is designed and the fuzzy control rule is obtained based on test data and expertise to ensure that the braking system can restrain gear walk effectively.

The structural schematic diagram of anti-skid braking control system is shown in Fig. 9. The controller is a single variable two-dimensional Mamdani controller. One of the inputs of fuzzy controller is the same as the input of the reference speed-speed difference controller, namely, the difference between the reference speed and the wheel linear velocity $e$. The other input is its derivative $e^{\text{'}}=de/dt$. The output voltage of the fuzzy controller is the input of the brake apparatus. This kind of two-dimensional controller can reflect the dynamic behavior of the system and improve the braking control performance.

Fig. 8Simulation results of PID antiskid braking system

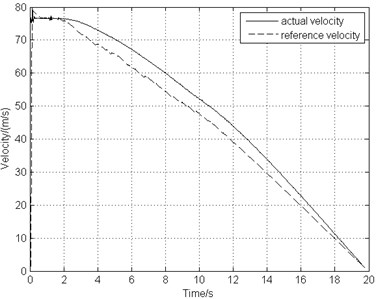
a) Aircraft speed

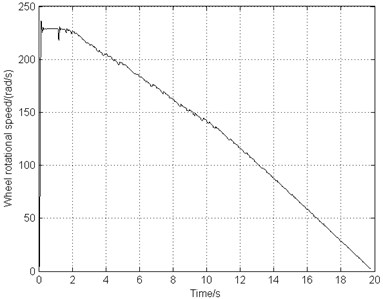
b) Wheel speed

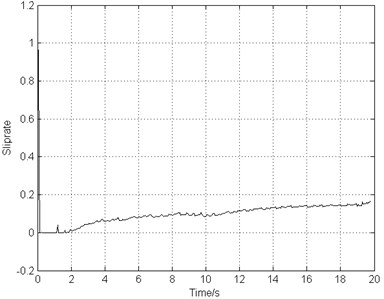
c) Slip rate

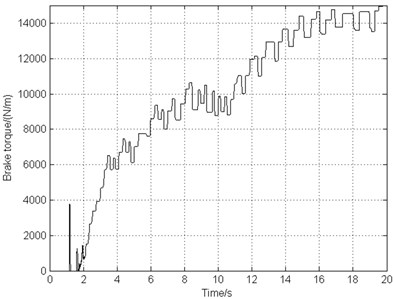
d) Brake torque

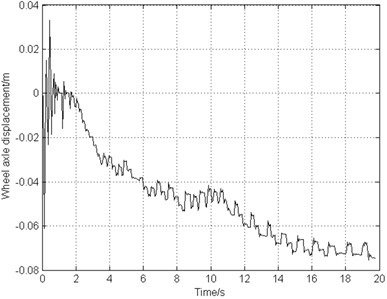
e) Longitudinal displacement of wheel axle

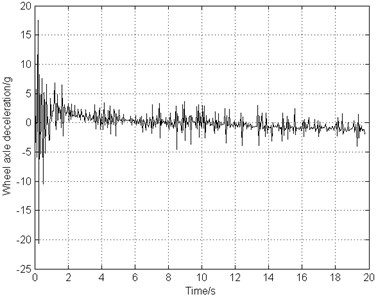
f) Longitudinal acceleration of axle wheel

5.1.1. Identifying inputs and outputs

The inputs and outputs are fuzzified and the fuzzy domains can be divided into 7 sets:

The difference between the reference speed and the wheel linear velocity $e$ is:

23

$e=\left\{NB,NM,NS,ZE,PS,PM,PB\right\}.$

The derivative of the velocity difference $e^{\text{'}}$ is:

24

$e^{\text{'}}=\left\{NB,NM,NS,ZE,PS,PM,PB\right\}.$

Fig. 9The structural schematic diagram of anti-skid braking control system

The output voltage $U$ is:

25

$U=\left\{NB,NM,NS,ZE,PS,PM,PB\right\}.$

The membership functions of every fuzzy set should be determined. In order to guarantee both the sensitivity and the robustness, selecting the membership functions needs several times of modification and is shown in Fig. 10. The membership functions of the two inputs are Gaussian-type, while the output is triangular type.

Fig. 10The fuzzy sets and the membership functions of variables

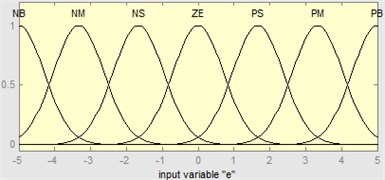
a) The fuzzy sets and the membership functions of input $e$

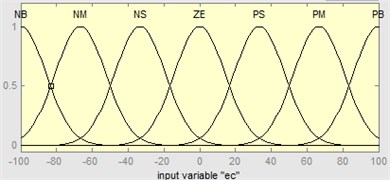
b) The fuzzy sets and the membership functions of input $e\text{'}$

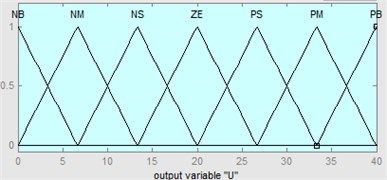
c) The fuzzy sets and the membership functions of output $U$

5.2. Simulation results and discussion

The landing operating condition is the same as the one used in Sections 3.2 and 4.2. The combined braking system starts to work after 1 second of landing. From Fig. 11(a) and Fig. 11(b), it can be seen that the airplane stops in 16 s, decreased by about 17 % comparing to the deceleration brake. The airplane keeps stable taxiing in a constant deceleration and the wheel rotating speed reduces steadily. Fig. 11(c) illustrates that the slip rate is close to the optimal value 0.15. This indicates that the frictional force between the ground and the tire reaches the maximum, bringing about higher braking efficiency. Fig. 11(d) shows that the braking frequency is very low ranging from 1 Hz to 2 Hz. Fig. 11(e) indicates that the vibration frequency approximately equals to the braking frequency and the gear walk average amplitude is only 2 mm. Fig. 11(f) demonstrates that the wheel axle longitudinal acceleration is located at 5 g. As time goes on, the acceleration decreases smoothly and the gear walk phenomenon converges in a stable state.

5.3. Comparison of the influence of two braking systems on gear walk

The modified combined brake and PBM reference speed-speed difference brake simulation results, related to gear walk characteristics are compared to the results of original deceleration brake in Table 3.

From Table 3, it can be seen that in the same landing and taxiing operating condition, the average wheel axle gear walk average amplitude decreases by 73 % under the control system of combined brake, and the only PBM brake system by 26 %. Meanwhile, the average wheel axle longitudinal acceleration peak value reduces by 65 % and 91 % respectively. In addition, the braking time is shortened by 17 % of combined system and the PBM system almost remains the same. This indicates that not only the braking efficiency is improved but also the braking frequency drops sharply by the new combined system, much better than the improvement of the only PBM system. The modified braking system works more steadily and is able to protect the braking apparatus. Due to lower braking frequency, the vibration frequency of gear walk also decreases by 59 %, making the vibration gentler. Therefore, the gear walk phenomenon is weakened effectively by the modified combined braking control system.

Fig. 11Simulation results of combined braking system

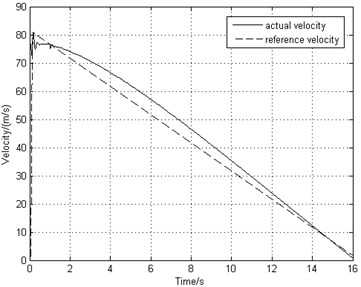
a) Aircraft speed

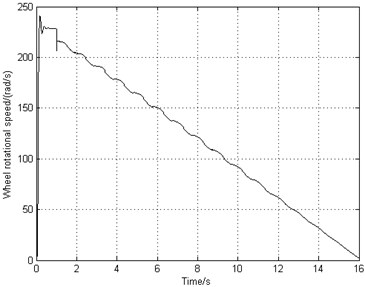
b) Wheel speed

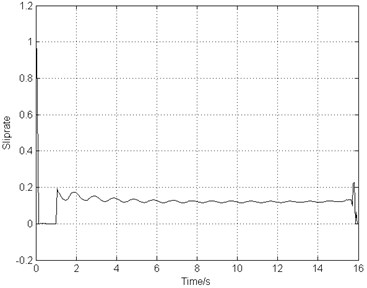
c) Slip rate

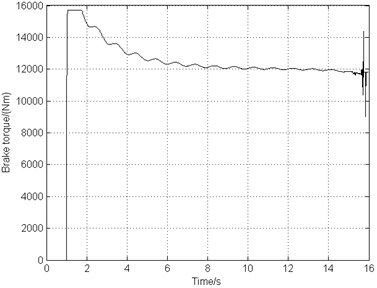
d) Brake torque

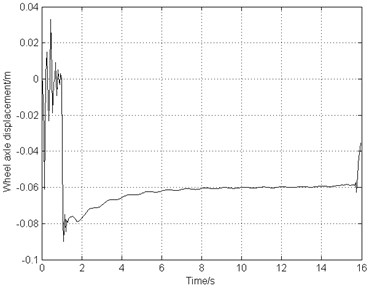
e) Longitudinal displacement of wheel axle

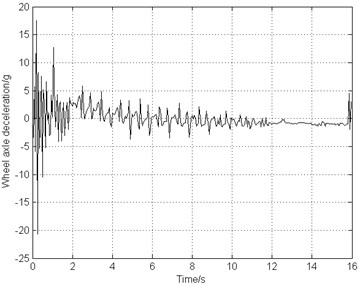
f) Longitudinal acceleration of axle wheel

6.1. Runway surface

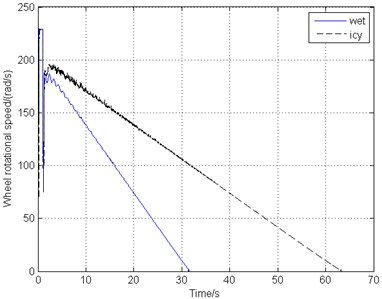
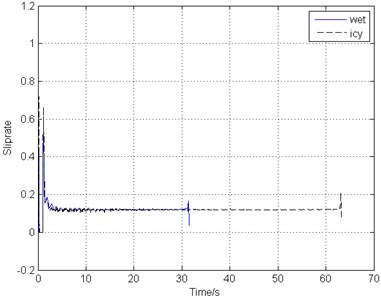
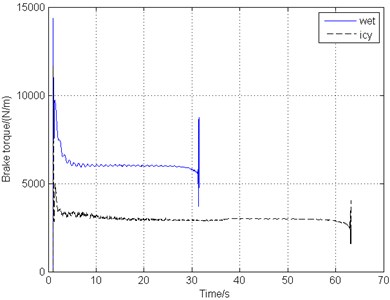
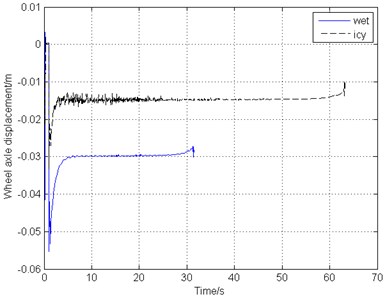
Due to different weather change, the runway would become wet or icy, leading to the drop of the friction coefficient between the ground and the tire. The friction coefficient value varies according to Eq. (5). Fig. 12 shows the simulation results of the braking response and gear walk performance when the runway surface is wet and icy, with other operating conditions remaining unchanged.

Fig. 12Simulation results of different runway surfaces

a) Wheel speed

b) Slip rate

c) Brake torque

d) Longitudinal displacement of wheel axle

As can be seen in Fig. 12(a), the aircraft could stop in 32 s and 63 s on wet and icy runway respectively. With the decrease of the friction coefficient of the runway as the largest coefficient drops from 0.8 to 0.4 and 0.2, the braking time multiples. However, Fig. 12(b) shows that even though a step response appears at the start of braking and there is some fluctuation during the first half of the whole process, the wheel velocity, the braking torque and gear walk vibration converge to a constant and the vibration is gentle. Fig. 12(c) and Fig. 12(d) illustrate that on the icy runway, the main landing gear vibrates a little more fiercely than it on the wet and dry runway with a higher gear walk frequency, while the vibration and the brake torque amplitudes are both lower due to the smaller friction force on the ground. A large span of the friction coefficient variation indicates that the proposed combined braking control system performs well and is of good adaptability.

6.2. Landing gear strut longitudinal stiffness

Gear walk, caused by several external and internal factors, is a longitudinal vibration on the landing gear. Therefore, the longitudinal stiffness of the main landing gear strut is one of the most important internal factors and has great impact on gear walk. Fig. 13 demonstrates the braking response and gear walk performance under different strut longitudinal stiffness ranging from –20 % to +20% change of the original structure stiffness.

Fig. 13Simulation results of different landing gear strut longitudinal stiffness

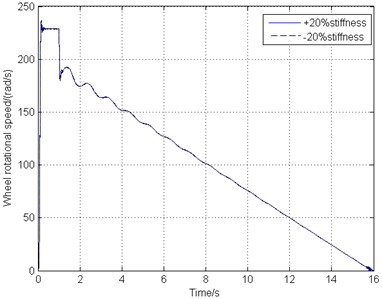
a) Wheel speed

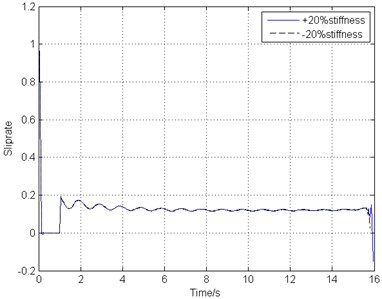
b) Slip rate

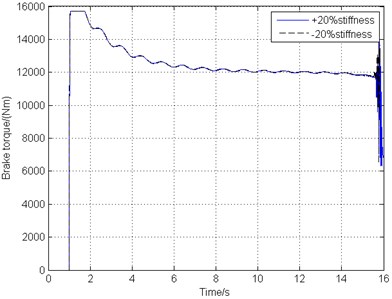
c) Brake torque

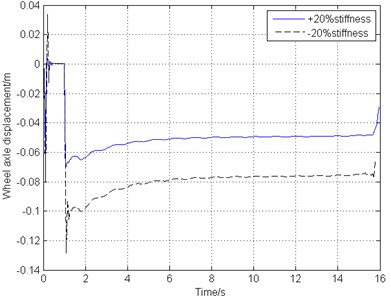
d) Longitudinal displacement of wheel axle

From Fig. 13, it can be seen that the internal factors variation such as the landing gear strut longitudinal stiffness does not have any influence on the brake response. Fig. 13(a), (b), (c) indicate that the combined braking control law is also stable in this landing gear system no matter how the landing gear strut structure changes. Fig. 13(d) shows that as the decreasing of the strut longitudinal stiffness, gear walk amplitude becomes larger, but the vibration frequency and trend stay the same.

6.3. Brake disks friction coefficient

Brake apparatus is also one of the most significant part in braking system, working together with braking control laws to stop the aircraft within the required time and distance safely. Possible fluctuant hydraulic pressure and worn-down with use of the brake disks would take place during the braking process, requiring the braking control system’s good robustness to ensure the aircraft security. Fig. 14 shows the simulation results under ±20 % friction coefficient variation between the brake disks contact surfaces.

Different friction coefficient between brake disks results in different braking torque under the control system output. Fig. 14 shows that larger brake torque lead to shorter braking time but a little fiercer fluctuation of the tire, braking torque and gear walk vibration at the first half section of the whole process. However, after the adjustment of the braking control law, the gear walk tends to vibrate gently and remain smooth, indicating that this combined control law possesses good stability and robustness.

Fig. 14Simulation results of different brake disks friction coefficient

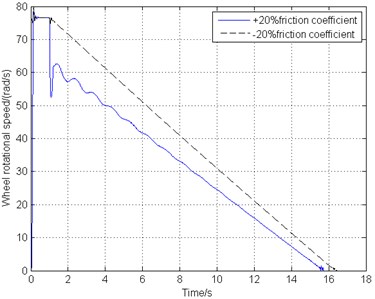
a) Wheel speed

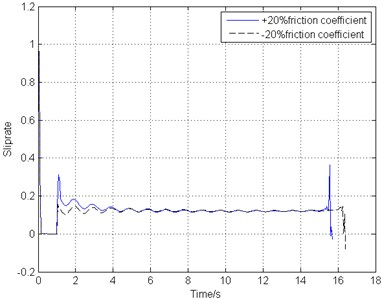
b) Slip rate

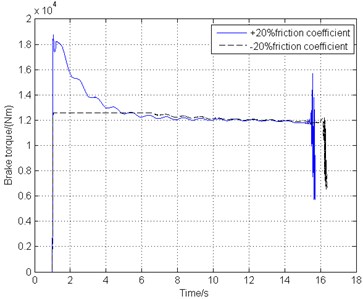
c) Brake torque

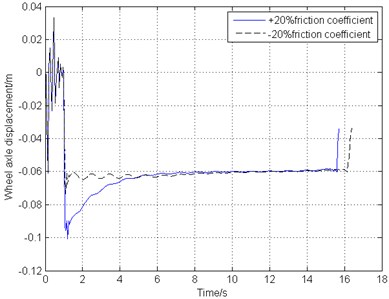
d) Longitudinal displacement of wheel axle