Dynamic modeling of spindle-rolling bearings systems in peripheral milling operations

1. Introduction

Commonly used in machining processes the high speed milling (HSM) machines have an important place in industrial manufacturing. They are characterized in fact by low cutting forces and high material removal rate to lead to quality of the product and closer tolerances. Unfortunately, the process instability affects badly the product finish surface and reduces dimensional accuracy and increases the rate of tool wear and may leads to the breakage of the spindle-tool unit.

Large displacement of the tool is the origin of high noise and rapid wear of both cutting tool and machine tool. It is the result of chatter arising from multiple causes and the most important one is called regenerative chatter produced by the regeneration of the work piece surface waviness.

This instability phenomenon called chatter is widely studied by [1-4] to leads to the development of the stability lobes diagrams in milling process which allow to choose the maximum axial depth of cut for a given spindle speed associated with a chatter free machining.

Altinas and Budak [5-7] developed a stability method which leads to analytical determination of stability limits. The method was verified by experimental and numerical results and applied to the stability of ball end milling then extended the frequency domain stability models to cutters with arbitrary geometries [8] and to variable pitch cutters [9] and prediction of surface location errors in flexible milling systems [10]. The major efforts of these researches focus on specific cutting force identification and chatter avoidance and determination of cutting conditions with a maximum of material remove rate.

Many authors have investigated analytically and experimentally the dynamic behavior of machine tool spindle-bearing systems. They show that spindle dynamics are influenced by a large number of factors such as holder characteristics [11] and spindle shaft geometry and drawbar force [12] as well as the stiffness and damping provided by the bearings [13]. Contrary to bearing properties and spindle rotor dynamics which depend on spindle speed most of these factors are independent of spindle speed and rotating systems have been successfully modeled through rotor-dynamics studies [14, 15].

Several previous research works considered that over a full spindle speed range the dynamic characteristics of the spindle-tool set do not change substantially. However, for high speed milling operations there will be changes due to gyroscopic moments and centrifugal forces on both bearings and spindle shaft which will give rise to variation in dynamic behavior of the spindle set. Several other factors influence this behavior such as holder characteristics and spindle shaft geometry and drawbar force which are independent of spindle speed [16-18]. A high speed electro-spindle supported by rolling bearings has been designed and modeled by Patil et al. [19]. They have presented an analytical model for predicting the effect of a localized defect on the ball bearing vibrations. The effect of the defect size and its location has been investigated. The numerical results obtained have been compared with experiments.

The bearings stiffness and damping factors are strictly related to loads and spindle speed [20]. In this context Nelson [21] developed a rotor-bearing model of the spindle set using Timoshenko beam theory taking into account shear deformation. His formulation has been used by Rantatalo et al. [22] for stability predictions and to validate experimental approaches of a milling machine spindle.

Kang et al. [23] analyzed the effects of design parameters on static and dynamic performance of spindle-bearing systems by using Finite Element Method (FEM). The parameters considered in their case studies included journal diameter and span ratio and bearing stiffness for static performance but for dynamic performance only the bearing stiffness was considered. The only high speed effect included in their FEM was gyroscopic moments. Li and Shin [24] published a paper to investigate the effects of bearing configuration on the dynamics of high speed spindles. An integrated Finite Element Method (FEM) model has been developed by Lin and Tu [25] to combine the changes of the bearing stiffness and shaft rigidity to determine the overall spindle-bearing system dynamics.

In the previous theoretical studies, the spindle was considered as flexible or rigid bodies but in our study the flexible and the rigid motions are combined. The finite element modeling is developed to study a real system case. The nonlinear forces exerted by rolling bearings on the inner races based on the Hertz contact theory and the dynamic cutting forces for milling operation are formulated. Using Lagrange formalism, the dynamic equation of motion is obtained taking into account the centrifugal force and gyroscopic moments. The implicit Newmark algorithm coupled with Newton Raphson iterative method is used to solve the nonlinear differential equation iteratively in order to analyze the influence of some parameters on the dynamic response of the spindle.

2. Modeling of spindle machining

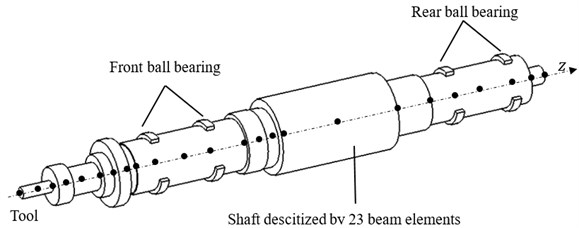
The study consists on analyzing structural vibrations generated by HSM spindle supported by four ball bearings (two front bearings and two rear bearings) as shown by Fig. 1. Bearings outer races are fixed in the rigid support (logging) while the inner races are rigidly assembled to the rotating shafts. The spindle is discretized to 23 beam elements using the Timoshenko theory taking into account both elastic and rigid motion. The centrifugal effect and the gyroscopic moment are taken into account. The bearing unbalance and cutting effects are defined as forces exerted on the spindle and their expressions are detailed in the next sections.

Fig. 1Spindle-tool system modeling

2.2. Rolling bearing modeling

The bearings effects are introduced as forces and moments. In fact, each rolling bearing placed in the $k$th node, exerts forces and moments computed using the Hertz contact theory [13]:

3

$\left\{\begin{array}{l}{F}_x^k\\ F_y^k\\ M_x^k\\ M_y^k\end{array}\right\}\mathrm{}\mathrm{}=\mathrm{}\mathrm{}{{\sum }_{j=1}^{N_{ball}}-K\left({\mathrm{\Delta }}_j^k\right)}^{1.5}\left\{\begin{array}{c}\mathrm{c}\mathrm{o}\mathrm{s}{\psi }_j^k\mathrm{c}\mathrm{o}\mathrm{s}{\alpha }_j^k\\ \mathrm{s}\mathrm{i}\mathrm{n}{\psi }_j^k\mathrm{c}\mathrm{o}\mathrm{s}{\alpha }_j^k\\ R_j\mathrm{s}\mathrm{i}\mathrm{n}{\psi }_j^k\mathrm{s}\mathrm{i}\mathrm{n}{\alpha }_j^k-\left(\frac{D}{2}\mathrm{s}\mathrm{i}\mathrm{n}{\alpha }_0\right)\mathrm{s}\mathrm{i}\mathrm{n}{\psi }_j^k\mathrm{c}\mathrm{o}\mathrm{s}{\alpha }_j^k\\ -R_j\mathrm{c}\mathrm{o}\mathrm{s}{\psi }_j^k\mathrm{s}\mathrm{i}\mathrm{n}{\alpha }_j^k+\left(\frac{D}{2}\mathrm{s}\mathrm{i}\mathrm{n}{\alpha }_0\right)\mathrm{c}\mathrm{o}\mathrm{s}{\psi }_j^k\mathrm{c}\mathrm{o}\mathrm{s}{\alpha }_j^k\end{array}\right\},$

where, ${\psi }_j^k$, ${\alpha }_j^k$ and $R_j$ represent respectively the ball angular position the loaded contact angle and the radial position of the outer race curvature centre of the $j$th ball in the $k$th rolling bearing. $N_{ball}$ and $K$ are respectively the balls number and the Hertz contact constant deduced from curvature radius of the elements in contact. ${\mathrm{\Delta }}_j^k$ is the elastic deformations of the $j$th ball [13] given by:

4

${\mathrm{\Delta }}_j^k=\left(d\left({\psi }_j^k\right)-d_0-C_r\right)\times H_{\mathrm{0,1}},$

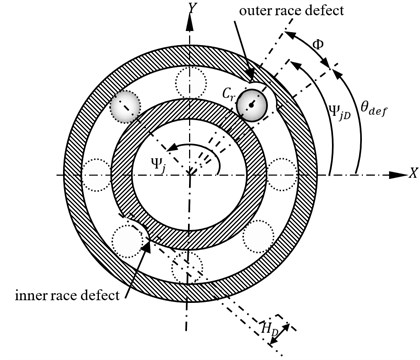
where $H_{\mathrm{0,1}}$ is the Heaviside function while $d\left({\psi }_j^k\right)$ and $d_0$ are respectively the loaded and unloaded distance between inner and outer races curvature centers for each rolling element $j$. $C_r$ is a scaling default of an inner or an outer race as shown by Fig. 2. This defect is defined by [19] as a half sinus written as following:

5

$C_r^{}=H_D\mathrm{s}\mathrm{i}\mathrm{n}\left(\frac{\pi }{{\delta }_D}\left({\psi }_j-{\psi }_{jD}\right)\right),$

with $H_D$ is the defect height and $\varphi$ is the defect size and ${\psi }_{jD}$ denotes the defect position written for inner and outer race respectively as:

6

${\psi }_j-{\psi }_{jD}=\left\{\begin{array}{l}{\omega }_{c}t+\frac{2\pi }{N_{ball}}\left(N_{ball}-j\right),O.R,\\ \left({\omega }_c-{\omega }_i\right)t+\frac{2\pi }{N_{ball}}\left(N_{ball}-j\right),I.R.\end{array}\right.$

The total actions exerted by the bearings on the spindle in all system degrees of freedom will be the sum of the forces exerted by each rolling bearing given by Eq. (3).

Fig. 2Defected ball bearing modeling

2.4. Cutting force modeling

To take into account, in our study, the contribution of all the forces of each element of each cutting edge in cutting process, the cutting edge is discretized using a mechanical approach. Indeed, the cutting forces model on one differential element takes into account the shearing forces and the edge forces by means of a tangential and radial component as shown by Fig. 3. These components depend on the correspondent cutting coefficients as well as the instantaneous chip thickness $h$ and the differential width of cut $dz$.

Consider a cutter element $k$ with a differential height $dz$ at axial location $z=kdz$ of flute number $j$. The instantaneous chip thickness $h_j\left(t,z\right)$ removed by the differential cutting edge element is defined as:

8

$h_j\left(t,z\right)=\left(f_t+u_x\left(t,z\right)-u_x\left(t-\tau \right)\right)\mathrm{s}\mathrm{i}\mathrm{n}\left({\varphi }_j\left(t,z\right)\right)$
$-\left(u_y\left(t,z\right)-u_y\left(t-\tau \right)\right)\mathrm{c}\mathrm{o}\mathrm{s}\left({\varphi }_j\left(t,z\right)\right),$

where $f_t$ is feed-per-tooth and $u_x(t,z)$ and $u_y(t,z)$ are deflections of tool-tip at the present time and $u_x(t-\tau )$ and $u_y(t-\tau )$ are deflections of tool-tip at the previous time. The delay between is defined as follow:

9

$\tau =\frac{2\pi }{\mathrm{\Omega }N},$

with $N$ the is the number of teeth of the tool.

Fig. 3Elemental cutting forces of peripheral milling

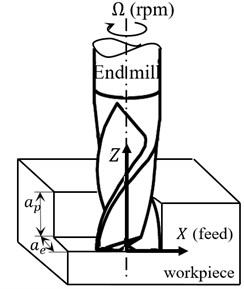
a) Milling operation

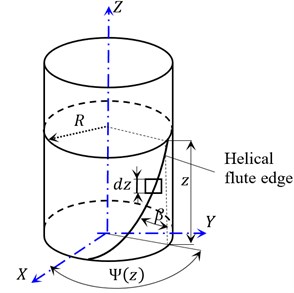
b) Helical flute edge geometry

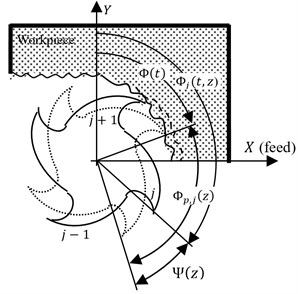
c) Schematic representation of the geometrical parameters

d) Differential tangential and radial forces

The instantaneous immersion angle of the cutting edge for the flute $j$ at elevation $z$ at time $t$ is expressed by:

10

${\varphi }_j\left(t,z\right)=\varphi \left(t\right)+{\varphi }_{p,j}\left(z\right)-\psi \left(z\right),$

where $\varphi \left(t\right)=\mathrm{\Omega }t$ is the angular position of the reference flute ($j=$ 0) at elevation $z=$ 0.

The lag angle between the flute tip and edge at elevation $z$ is $\psi \left(z\right)=z\mathrm{t}\mathrm{a}\mathrm{n}\beta /R$ and the pitch angle is ${\varphi }_{p,j}\left(z\right)=2\pi \left(j-1\right)/N$ for cutters which have constant helix angle ($\beta$), tool radius ($R$), and pitch angles.

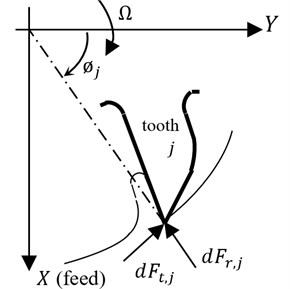
For a point on the ($j$th) cutting tooth the differential milling forces corresponding to an infinitesimal element thickness ($dz$) in the tangential direction $d{F}_t$, and radial direction $d{F}_r$ is given by:

11

$d{F}_{t,j}=g\left({\varphi }_j\left(t,z\right)\right)K_t{h}_j\left(t,z\right)dz,d{F}_{r,j}=g\left({\varphi }_j\left(t,z\right)\right)K_r{h}_j\left(t,z\right)dz,$

where $K_t$ and $K_r$ are respectively the tangential and radial specific cutting forces and $g\left({\varphi }_j(t,z)\right)$ is a step function which is used to illustrate whether the current differential cutting edge is involving in cutting process or not and can be expressed by:

12

$g\left({\varphi }_j(t,z)\right)=\left|\begin{array}{ll}1,& {\varphi }_{st}<{\varphi }_j\left(t,z\right)>{\varphi }_{ex},\\ 0,& \text{otherwise},\end{array}\right.$

where ${\varphi }_{st}$ and ${\varphi }_{ex}$ are the entry and exit angles of the cutter.

Through coordinate transformation the cutting forces in the global coordinate system can be evaluated as following:

13

$\left\{\begin{array}{l}d{F}_x\left(t,z\right)\\ d{F}_y\left(t,z\right)\end{array}\right\}=\left[\begin{array}{cc}-\mathrm{c}\mathrm{o}\mathrm{s}\left({\varphi }_j\left(t,z\right)\right)& -\mathrm{s}\mathrm{i}\mathrm{n}\left({\varphi }_j\left(t,z\right)\right)\\ \mathrm{s}\mathrm{i}\mathrm{n}\left({\varphi }_j\left(t,z\right)\right)& -\mathrm{c}\mathrm{o}\mathrm{s}\left({\varphi }_j\left(t,z\right)\right)\end{array}\right]\left\{\begin{array}{l}d{F}_{t,j}\left(t,z\right)\\ d{F}_{r,j}\left(t,z\right)\end{array}\right\}.$

By integrating along the axial depth of cut and summing for all in-cut teeth the overall cutting forces acting on the cutter for a certain indexed angle can be given as:

14

$\left\{\begin{array}{l}{F}_x\\ F_y\end{array}\right\}=\mathrm{}\left\{\begin{array}{l}{\sum }_{j=1}^{N_f}{\sum }_{k=1}^{N_z}\mathrm{‍}d{F}_x\left(t,z\right)\\ {\sum }_{j=1}^{N_f}{\sum }_{k=1}^{N_z}\mathrm{‍}d{F}_y\left(t,z\right)\end{array}\right\},$

where $N_f$ and $N_z$ are respectively the number of teeth and the number of cutter elements in $Z$ direction.

3. Numerical results and discussion

The Newmark method coupled with the Newton Raphson iterative method is used to resolve the nonlinear equation of motion Eq. (15). Both rigid and elastic displacements are taken into account in all numerical results.

Characteristics of healthy rolling bearing are cited in Table 1 and used to validate the model for a milling operation whose parameters are listed, also, in the same table.

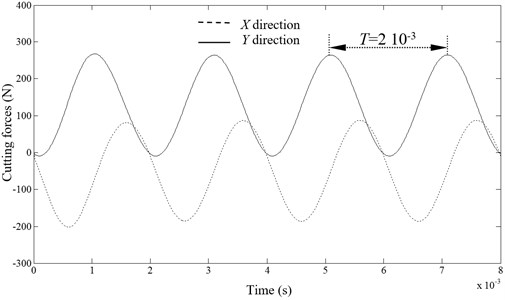
Fig. 4 presents the cutting forces in both $X$ and $Y$ directions, for a system rotating velocity equal to 15000 rpm. We note a sinusoidal behavior for both forces having 500 Hz as frequency (2×10^-3 as period). In fact, this last correspond to 2×$f_r$, double rotating frequency, originating from the tool teeth number (2 teeth). The cutting force in the normal direction is bigger than the force in the feed direction. But, the peak to peak amplitude remains constant. Those results are confirmed with experimental ones given by Faassen [2].

Fig. 4Cutting forces direction

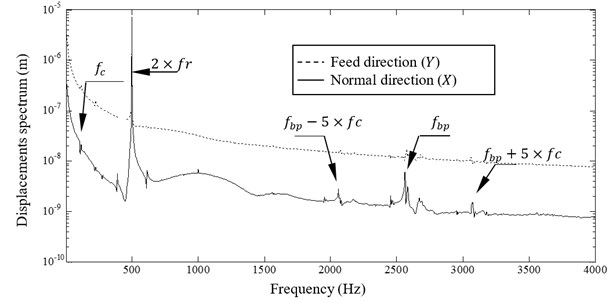
By examining the Fourier transform of the normal and feed displacements of Fig. 5 we note the presence of a dominant peak occurring at 2×$f_r$ caused by the cutting force variation in time as shown by Fig. 4. Another peak appears at $f_{bp}=$ 2562 Hz corresponding to ball passage frequency of the rear and front bearings which has a lower vibratory level. This last provides from the variation of the angular position of balls when the bearings are in movement, which causes the variation of the total external load in time (when each bearing rotates one round/$N_{ball}$). The lowest level peak at $f_c=$ 111.4 Hz corresponds to the cage frequency (corresponding to one round balls rotation). Their harmonics are also observed. We note also a modulation between the ball passage frequency and the cage frequency $f_{bp}\pm K{f}_c$.

Fig. 5X and Y directions displacements

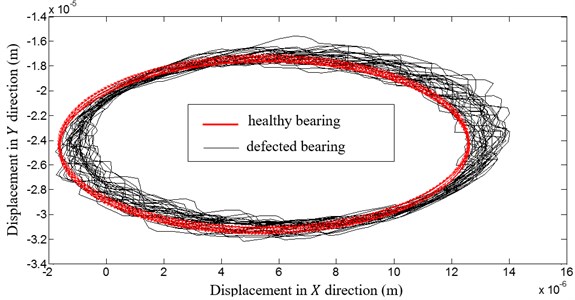
We introduce now an outer race default, as defined in Section 2.2., having a defect height $H_D=$ 10^-6 m, a defect size $\varphi =$ 0.1778×10^-3 and a null initial position. When we examine the orbit of the milling tool for the two cases: healthy and defected bearings (given by Fig. 6), we note an excessive fluctuation of the orbit for a defected rolling bearing case, which causes a bad quality surface of the milled workpiece. We note, also, for a bearing default case, a shifting in the orbit center in $X$ direction. This shifting is better viewed in Fig. 7, presenting the first node displacement in $X$ direction for the two cases. In fact, this shifting equal to 10^-6 m is equal to the default height.

Fig. 61st node orbit

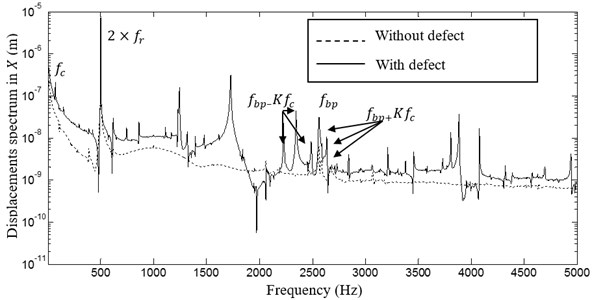
The FFT transform of first node displacement in $X$ direction for the healthy and unhealthy bearings is given by Fig. 8. By examining the spectrums, we note a higher vibratory level in the defected case. Also we remark an increase in the ball passage frequency level. In fact, the defect is periodic with a frequency equal to the ball passage frequency. The modulation between the ball passage frequency and the cage frequency is very important in the defected case which causes an excessive displacement fluctuation (as observed in Fig. 6) translated to a bad quality surface as observed in reality.

Fig. 71st node displacement in X direction (with and without defect)

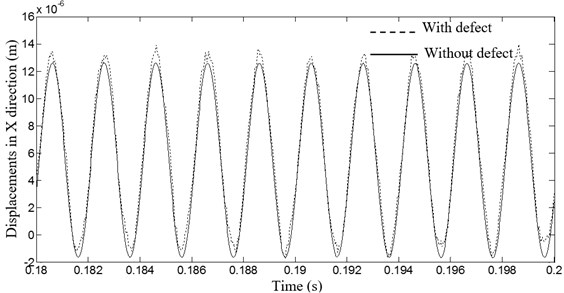
Fig. 8Spectrum of the 1st node displacement in X direction (with and without defect)

In order to show the bearings characteristics incidence, we choose NHBB#CXMC-1112DXC77 as front bearings with the characteristics by given in Table 1 and NHBB#CXMC-1109DXC77 as rear bearings with the same contact angle and a ball number equal to 19. The pitch and ball diameters are respectively 60 mm and 7.94 mm. A comparison between the spectrums of the 1st node displacement in $X$ direction of different and identical studied bearings is given in Fig. 9. The dominant frequency corresponding to the running frequency is noted in the two study cases. The ball passage frequencies of each rolling bearing are observed in the case of different bearings which appear at 2562 Hz and 2071 Hz. The two cages frequencies and the modulation are also viewed.

Fig. 9Spectrum of the 1st node displacement in X direction (different and identical bearing)

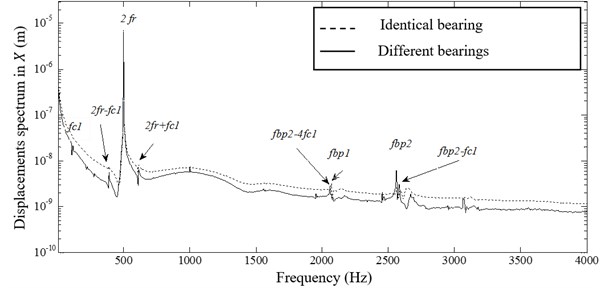
Fig. 10Influence of the number of cutter teeth on the displacements

Fig. 11Time response of the displacement along X axis

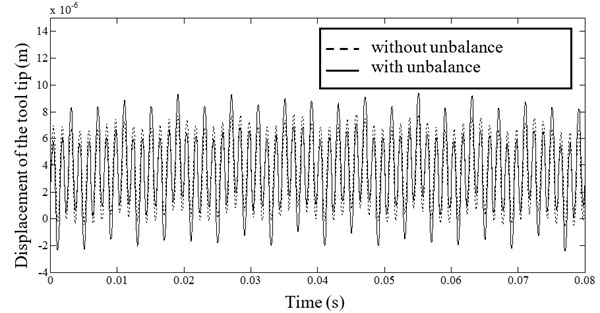
Fig. 12Frequency spectrum of the displacement along the X axis for a system with and without unbalance

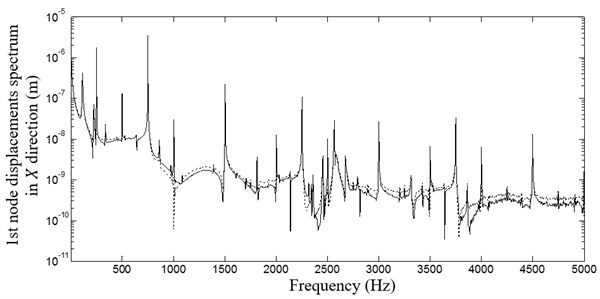
Fig. 10 presents the spectrum of the 1st node displacement in $X$ direction for identical bearings and different cutter teeth values $N$ which vary from 2 to 4. The dominate frequency producing at $N\times f_r$ is always observed (as explained for Fig. 5) but the vibratory level is decreasing when the teeth number is increasing. Indeed, the total cutting force is sheared between the teeth. Then the generated force by each tooth on the manufactured part (i.e. the shock on the spindle) decreases when the teeth number increases.

A comparative study for a spindle with and without unbalance is investigated with a teeth number $N$ equal to 3 and identical rolling bearings. The time response of the displacement in $X$ direction of the tool tip is shown by Fig. 11. The maximum response of the tool tip in absence of unbalance is 7 µm but it reaches 8.2 µm when we introduce an unbalance. Both of vibratory levels have the same period of time. By higher vibration levels unbalanced spindle promotes maximum form errors on finished surface of manufactured part which is in concordance with the reality.

By examining the spectrum of respective displacements in Fig. 12 we note the presence of the cutting frequency produced at 750 Hz. The ball passage and the cage frequencies are also founded. For the system having an unbalance we note also the presence of the rotating shaft frequency corresponding to 500 Hz.

4. Conclusion

A dynamic modeling of high speed spindle supported by rolling bearings is established in the case of high speed milling process. Using the finite element method, we consider the gyroscopic effect as well as the centrifugal forces and the coupling between rigid and elastic modes in the global equation of motion. The implicit Newmark algorithm coupled with Newton Raphson iterative method is used to solve the nonlinear differential equation of motion.

The cutting force model was used to predict the forces acting on the tooltip during peripheral milling process. The results of this simulation show a sinusoidal behavior and the cutting force in the normal direction is larger than the force in the feed direction. The examination of the spectrum of the normal and feed directions shows the presence of three characteristics frequencies such as two times the running frequency and the cage frequency and the ball passage frequency. The orbit of tool tip in $X$-$Y$ plane was plotted with healthy and defected bearings. The presence of defects causes an excessive vibrations and the modulation between the ball passage and the frequencies were more important. Simulated results show also that the number of cutter teeth strongly affects the frequencies contents of the tooltip.