Abstract
In this paper, the in-plane (IP) and out-of-plane (OP) interaction of masonry infill walls with various length-to-height ratios and vertical forces from dead and live loads are studied. For this purpose, calibrated numerical simulation for IP and OP behaviors of infilled frames has been exploited. In this method, first, the vertical loads are applied, then increasing IP displacement is imposed at the top of the models and finally OP demands are applied to the walls up to their failure. Two different methods of applying OP loading are studied: increasing static uniform pressure on the wall, and increasing dynamic acceleration. Three levels of IP displacement demands are considered: at the first reduction of tangential stiffness for IP force-displacement response, at the maximum IP strength, and at the displacement related to 20 % reduction of IP strength. The results obviously show that up to the point of the maximum IP strength capacity, the OP behavior of the considered models slightly enhanced due to the effects of improved arching actions originated from the development of IP compressive diagonal struts. Moreover, slight differences exist between the static and dynamic loadings in OP direction, hence proving the accuracy of the equivalent static loading in determining OP capacity for the studied infilled frames. Comparing the results of masonry infilled frames with those of the corresponding masonry walls indicate that the IP displacements negatively affect the OP strength in the latter, even at small IP displacement demands; however, the rate of OP strength reduction in larger IP drift ratios is lower compared to that of the corresponding infilled frame.
1. Introduction
Indeed, one of the most drastic challenges in the evaluation of many existing frame buildings is the understanding of real seismic performance of their infill wall elements. Nonetheless, coding methodology aimed at tackling this challenge is rather simple and adopts the commonly-argued concept of allocating the capacity for infilled frames as two distinct modes i.e. in-plane and out-of-plane modes. However, there is no doubt that these two sets of behaviors interact with each other and can therefore have a substantial influence on each other. There are several studies indicating the vulnerability of these structural elements in the out-of-plane (OP) direction [1, 2]. Angel and Abrams [3] stated that the OP capacity of masonry infilled reinforced concrete frames can reduce to half as a result of in-plane displacements and such dependency is more visible in high slenderness ratios. Kuang and Yuen [4] concluded that OP loadings on masonry infilled reinforced concrete frames can reduce their in-plane (IP) capacity up to 30 %. This result opposes with Alinejad’s [5] which shows an insignificant IP capacity reduction of the OP damages; while stating that the opposite is more important. The experimental results of Flanagan and Bennett [6] on masonry infilled steel frames proved that consecutive loading of masonry walls in IP and OP directions has little effect on their capacities; however, concurrent loading results in over 40 % reduction in IP capacity due to OP loading which is equal to 57 % of its capacity. There are also other numerical works with the aim of simulating IP and OP interaction of infill walls by simple strut models, among which Kadysiewski and Mosalam [7] and Hashemi and Mosalam [8] can be cited.
In this paper, the effect of different IP displacement levels on the OP capacity for infilled frames is studied through utilizing the calibrated finite element analysis both for IP and OP response. Two distinct aspect ratios (the ratio of wall’s height to its length) are selected for the models in order to evaluate the dependency of this parameter to OP capacity. Also, the two states of vertical loading including models with and without vertical loads on the top beam as well as the columns which represent the dead and live loads are utilized to study the consequent effects of interactive behaviors in the infilled frames under study. Two different OP loading demands are considered: seismic loading and the equivalent uniform pressure on the wall. For seismic loading, a set of seven earthquakes with increasing intensity is considered. The proposed Endurance Time (ET) function is also exploited for comparison purposes. The results in terms of OP strength reduction due to IP demands are elaborated and compared with those of the corresponding studies in terms of IP-OP interaction curves.
2. Finite element calibration
In this part, seismic performance of two previously-tested infilled frames is simulated numerically using general-purpose finite element software ABAQUS [9]. The implemented method is simplified-micro in which bricks are modeled individually and the properties of mortar are taken into account by zero-length cohesive elements. Besides, to consider the mortar’s thickness, half of the mortar thickness is included in the bricks’ thickness. Because of the highly brittle and nonlinear response of infilled frames and the associated numerical convergence problems, the utilized numerical solving method is central difference. Therefore, the static loadings i.e. the vertical load, the IP displacement and the static OP uniform pressure are applied to the models under quasi static procedure by controlling the ratio of the kinetic energy to the input energy of the model to keep it less than 10 % throughout the analysis.
The utilized plastic flow is Drucker-Prager [10] with Lubliner et al. yield function [11] for masonry and concrete. For modeling steel, Von-Mises plastic flow is utilized with elastic-perfectly plastic behavior. Regarding concrete and bricks, first-order, reduced integration hexahedral continuum elements (C3D8R) are used. Beam elements (B31) and cohesive elements (COH3D8) are allocated to modeling steel rebars/hoops and mortar, respectively. Sensitivity analyses are performed on the models and the converged mesh size of 2 cm with two elements alongside the bricks thickness is selected. Using at least two elements alongside the thickness of bricks is crucial for preventing “Hour-glassing” numerical problem susceptible for first-order, reduced integration elements in which flexural stiffness is significantly underestimated. The utilized model for stress-strain of masonry prism and unconfined concrete is Kent and Park [12]. Furthermore, Mander [13] model is utilized for confined concrete inside the hoops in the frame members. The schematic stress-strain curves of masonry and concrete is illustrated in Fig. 1(a). In this figure, and represent the tensile stress and strain, respectively; signifies tensile strength; denotes the initial modulus of elasticity; and are tensile and compressive damages, respectively which control the unloading slope of the stress-strain response. These parameters are assumed to be in linear form increasing from zero (undamaged state) to unity (fully damaged state) regarding plastic strains. and are stiffness recoveries in tensile and compressive states, respectively which govern the stiffness of stress-strain response during transition between tensile and compressive zones. It is assumed that and are 0.0 and 1.0, respectively. These values indicate that the material is not affected by tensile damages when it moves from tensile to compressive regime; however, the compressive damages fully influence the tensile behavior upon transition from compressive to tensile states.
Quadratic stress criterion is used for damage initiation in mortar under shear and tensile behaviors as Eq. (1). Additionally, damage evolution of mortar () is regarded as an inverse exponential function with the power of 10 and ultimate relative displacement of 1mm as Eq. (2) as is schematically illustrated in Fig. 1(b) which shows interface element stress against relative displacements (tangential or normal) of adjacent bricks surfaces. Where and are tangential stresses; is normal stress; and are tangential strengths; is normal strength; is effective relative displacement during first failure, denotes effective relative displacement in complete failure, represents maximum effective relative displacement within loading history, α is damage evolution rate (non-dimensional parameter):
Fig. 1Behavior of concrete, masonry and mortar
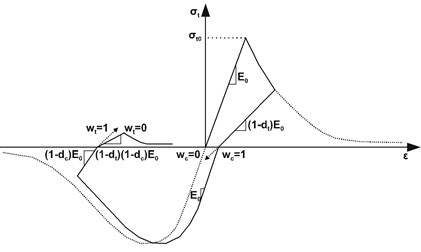
a) Stress-strain model of masonry and concrete
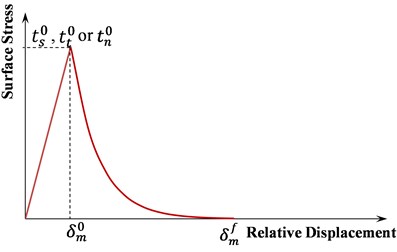
b) Mortar’s damage evolution mechanism
2.1. In-plane behavior
In order to calibrate the numerical models and assumptions under IP loading, the previously-performed experimental results by Mehrabi et al. [14] (Specimen 7) are chosen. Mechanical properties of mortar and bricks of the allocated specimen are presented in Table 1 except for the compressive strength of concrete in the surrounding frame which is 33.4 MPa. Also, the nominal yield strength and ultimate strength for the longitudinal reinforcement are 367 MPa and 449 MPa, respectively and those for the transverse reinforcement are 414 MPa and 662 MPa, respectively. Note that for numerical stability, the modulus for elasticity of the cohesive layer is assumed infinite and the modulus of elasticity of masonry prism is therefore assigned to the bricks. Where and are modulus of elasticity and compressive strength of masonry prism, respectively; is the Poisson’s ratio of masonry prism; is the tensile strength of bricks and mortar and is the shear strength of mortar; is the friction coefficient between bricks; and are tensile and shear softening energy per unit surface area, respectively. The geometrical characteristics of the numerical model parts and the meshed model are shown in Fig. 2.
Comparison between the experimental and numerical damages in the infilled frame of Mehrabi et al. [14] is shown in Fig. 3. In part (a) of this figure, the solid lines and the solid areas signify cracks and crushing in the masonry infill wall, respectively. The plastic stains in Part (b) of this figure are equivalent to the observed damages with the gray color denoting the severest damages. The force-displacement curve of the numerical models and the backbone of the experimental curve are presented in Fig. 4. As it can be seen, the numerical model can accurately capture the stiffness, strength and ductility of the considered infilled frame.
Table 1Mechanical properties of bricks and mortar
Brick | Mortar | |||||||||
Linear | Nonlinear | Tension | Shear | |||||||
Compressive | Tensile | |||||||||
N/mm2 | N/mm2 | N/mm2 | N·mm/mm2 | N/mm2 | N·mm/mm2 | N/mm2 | N·mm/mm2 | |||
Mehrabi et al. [14] | 4200 | 0.15 | 13.57 | 1.40 | 0.42 | 0.51 | 0.02 | 1.28 | 0.88 | 0.13 |
Varela-Rivera et al. [15] | 1350 | 0.15 | 2.45 | 0.40 | 0.14 | 0.36 | 0.01 | 0.36 | 0.60 | 0.03 |
Fig. 2The numerical model after Mehrabi et al. [14]
![The numerical model after Mehrabi et al. [14]](https://static-01.extrica.com/articles/17259/17259-img3.jpg)
a) Model parts with dimensions
![The numerical model after Mehrabi et al. [14]](https://static-01.extrica.com/articles/17259/17259-img4.jpg)
b) Meshed model
Fig. 3Damage severity and propagation in Mehrabi et al. specimen
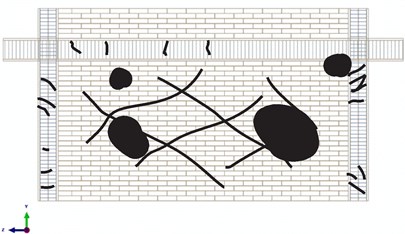
a) Failure mode in the experimental specimen [14]
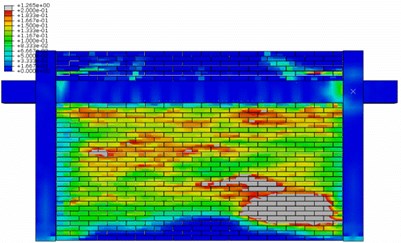
b) Plastic strain in the numerical model
Fig. 4Force-displacement curve of the benchmark model under IP loading after Mehrabi et al. [14]
![Force-displacement curve of the benchmark model under IP loading after Mehrabi et al. [14]](https://static-01.extrica.com/articles/17259/17259-img7.jpg)
2.2. Out-of-plane behavior
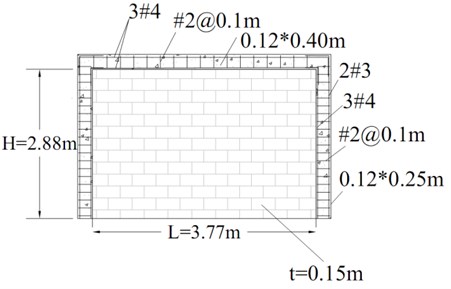
In order to calibrate the applied method of numerical simulation for infilled frames under OP loading, the experimental results carried out by Varela-Rivera et al. [15] (Specimen E-3) are taken into account. The mechanical properties of the allocated specimen are represented in Table 1 except for compressive strength of concrete in the surrounding frame which is 19.8 MPa and also the nominal yield strength for the longitudinal and transverse reinforcement as 412 MPa and 228 MPa, respectively. Fig. 5 depicts the model dimensions and representation (part (a) and (b), respectively) as well as the failure mode of the previously-tested specimen and the corresponding numerical mode (part (c) and (d), respectively) which clearly shows the potential lines of the concrete slabs due to confinement provided by the frame members. As observed in Fig. 6, along with the failure mode of the model which matches the experimental results, the force-displacement curve of the model is in close conformity to that of the experimental one.
Fig. 5Damage severity and propagation in Varela-Rivera et al. specimen
a) Specimen dimensions [15]
b) Model parts

c) Specimen’s failure mode
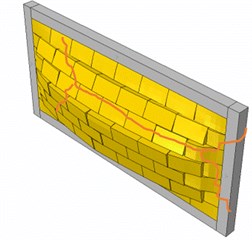
d) Model’s failure mode
Fig. 6Force-displacement of the benchmark model under OP loading after Varela-Rivera et al. [15]
![Force-displacement of the benchmark model under OP loading after Varela-Rivera et al. [15]](https://static-01.extrica.com/articles/17259/17259-img12.jpg)
3. Parametric study
In order to perform an in-depth study on the IP-OP interaction in infilled frames, a parametric study is performed on the abovementioned basic calibrated model of Mehrabi et al. [14]. Details of IP and OP excitation sequence of the models are shown in Fig. 7. According to this figure, the models’ self-weight as well as dead and live loads from the roof are initially applied to the models through body force and uniform pressure on the top beam, respectively. Then, the gradually increasing IP displacement demand is exerted at the top of models until it reaches one of the target levels explained below. In the last step, the models are excited in the OP direction whether by a uniform pressure on the infill wall or by time-history dynamic excitations; while keeping the targeted IP displacement constant through this step. Table 2 shows the parameters of the considered models for which the height of all the models are assumed 3.0 m. The parameters under study are the aspect ratio of the infill wall, and the effects of vertical loads on the top beam and the columns. While majority of the experimental and numerical studies do not take the effects of vertical loading from dead and live loads of the roof on the performance of infilled frames, few aimed at understanding the behavior of this structural systems with consideration of vertical loads [14, 16, 17]. It seems that large vertical loads on the infill walls can greatly influence their performance especially under OP loading. In other words, the confining effects of vertical loads can enhance the arching actions activated during OP deflection of these walls. Also, as far as the weak frame-strong infill is concerned, presence of vertical loads on columns can greatly decrease or increase their moment resisting capacity. In Table 2, and are height and length of model, respectively; is the concrete compressive strength in the frame. Other parameters have been previously defined.
Fig. 7Details of IP and OP excitation sequence
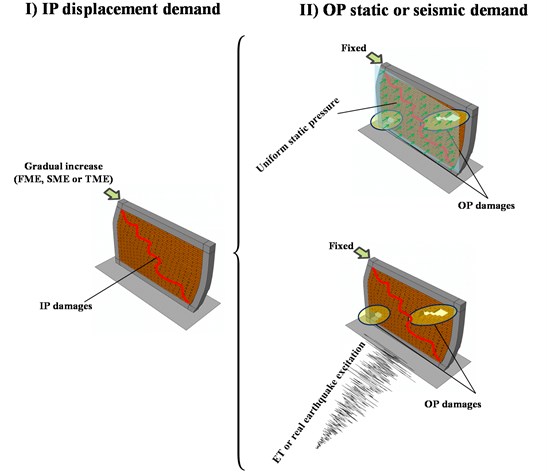
In this part, IP and OP interactions of the model infilled frames are studied in terms of failure modes and force-displacement behavior. The target of parametric study is to evaluate various types of damage due to IP displacement demands and also to explore the effect of such damages on the OP behavior of the infilled wall models. Based on the IP force-displacement diagrams of Fig. 8 idealized as the tri-linear backbone curve based on Haach et al. [18], three various levels of IP displacement (performance point) are selected for each wall. The first level is selected after the first major shear-sliding crack in the infill wall appears. The second and the third displacement levels are chosen as an ultimate strength capacity and the point related to 20 % drop in the strength of the model, respectively. These performance points can vary considerably depending on the characteristics of the considered infilled frames.
Table 2Model characteristics in parametric study
Model Name | (MPa) | (MPa) | (MPa) | Vertical stress on top beam (MPa) | Vertical stress on columns (MPa) | |
Model-1 | 0.50 | 13.5 | 33 | 1.3 | 0.72 | 0.36 |
Model-2 | 1.00 | 0.72 | 0.36 | |||
Model-1-No Surcharge | 0.50 | 0.00 | 0.00 | |||
Model-2- No Surcharge | 1.00 | 0.00 | 0.00 |
Fig. 8Performance points in a typical force-displacement diagram
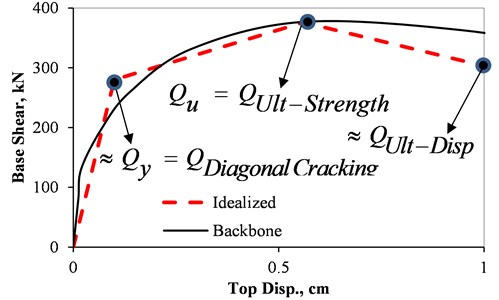
Fig. 9IP force-displacement curve of the models
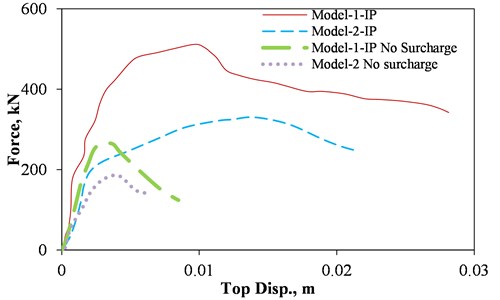
The force-displacement curve of the considered models under IP loading is shown in Fig. 9. As it can be seen, the vertical load significantly affects the behavior of the models, with up to 50 % increase in their strength capacity due to the effects of the applied vertical loads. Also, this effect has led to an increase in the effective stiffness of the model. Moreover, existence of vertical loads in both Model-1 and Model-2 resulted in a significant increase in the ductility. Note that increase in the strength, effective stiffness and ductility of the models because of vertical loads are comparable in both models which proves negligible sensitivity of this parameter to the aspect ratio of the infill wall. Therefore, it can be concluded that inclusion of vertical loads on the top beam and the columns can lead to performance improvement in different behavioral characteristics of infilled frames.
OP failure mode of the two representative models is depicted in Fig. 10. It is obvious from this figure that the crack patterns follow the potential lines as for the cracking in diaphragms. This proves the bi-directional arching action activated in the both models. Therefore, it can be stated that the both infill walls, regardless of their aspect ratio benefit from the effects of bi-directional arching action. It is noteworthy that the failure mode of other models follows the same pattern as for the two aforementioned models. In other words, the imposed IP displacement demand has marginal influence on the OP failure mode of the considered infilled frames. Also, the effects of vertical loads on the OP behavior of the models are not obvious; while this parameter per se is very influential in the IP response of such frames.
Fig. 10OP failure mode of the two representative models
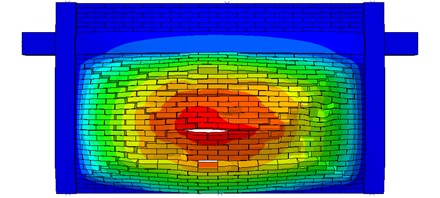
a) Model-1
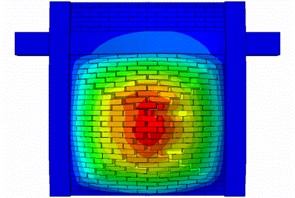
b) Model-2
Fig. 11OP static force versus mid-wall displacement under different IP demands
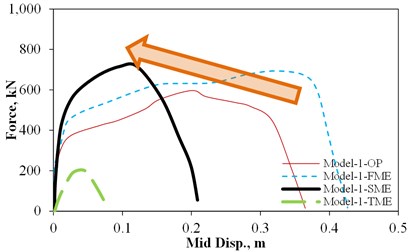
a) Model-1
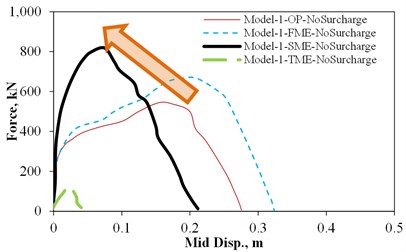
b) Model-1-No Surcharge
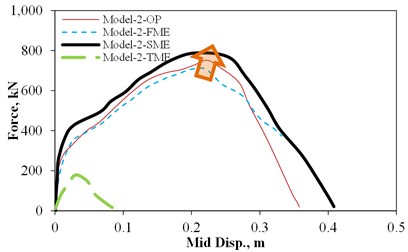
c) Model-2
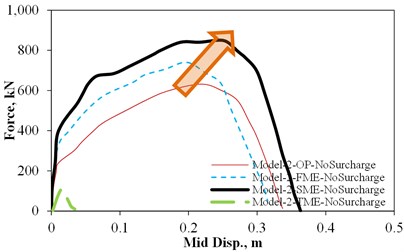
d) Model-2-No Surcharge
Fig. 11 shows the OP static force versus mid-wall displacement of models under different IP demands. There are three allocated IP displacement demand levels which have been applied prior to exertion of the OP demands. These levels include the First Major Event (FME) which is attributed to the first displacement at which the major reduction in tangential stiffness of the IP force-displacement response shown in Fig. 9 occurs. The second allocated IP displacement is the Second Major Event (SME) which is associated with the maximum strength capacity of IP force-displacement response of the models. The last applied IP displacement is the Third Major Event (TME) which is related to the IP displacement at which there is a 20 % reduction in the IP strength.
The interesting fact about the majority of the performed analyses is that the imposed IP demands on the infill slightly improve its OP strength capacity. This can be justified by the fact that these displacement demands result in compressive struts in the infill wall and providing the infill wall with confinement, which itself is the main cause of enhanced arching action. In this regard, the IP displacement demands have the same effects as for the vertical loads. This improvement in the OP capacity due to the IP displacements has not been observed in masonry walls without surrounding frames. However, this is not the case for large IP displacements where the OP capacity of the infill wall decreases dramatically because of the experienced IP damages on the wall in the form of corner crushing and the widened cracks.
4. Effect of dynamic loads
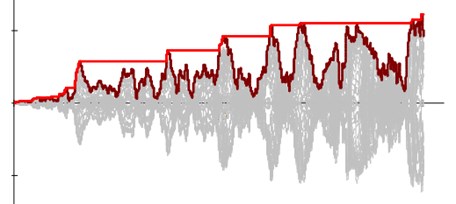
In this part, comparisons are made between the results of the previously-performed analyses with static OP loading and the corresponding dynamic loading. There is no doubt that the seismic response of any structure is significantly governed by strong motion characteristics of the applied ground motion known as strong motion parameters. To account for the substantial scattering of these parameters, seismic codes require applying several ground motions (at least three) on the studied structure when linear or nonlinear time-history analysis is to be performed [19, 20]. Furthermore, for calculation of Engineering Demand Parameter (EDP) of each building against any given seismic action with a definite Intensity Measure (IM), it is essential to execute Incremental Dynamic Analysis (IDA). Computation of this analysis can be very expensive for some structures including the models in this study which makes it infeasible. In response to this need, an innovative dynamic pushover procedure entitled Endurance Time (ET) proposed by Estekanchi et al. [21] is exploited. These increasing acceleration functions have been produced using numerical and optimization techniques. The main benefit of ET records is that their response spectrum at any time is linearly proportional to the response spectrum at a target time ( 10 sec) which is summarized in Eq. (3) and Eq. (4) and presented in Fig. 12. In these equations, “” is the natural period of the structure and is the codified acceleration spectrum. Consequently, “time” in these records is a critical factor for determining the intensity of excitation; the more a typical structure survives ET records, the more satisfactory is its seismic response. This is schematically shown in Fig. 13 which specifies Design A cannot meet codes requirements because the building collapses before reaching the targeted time. Besides, as it can be seen in Fig. 14, up to a specific time, the maximum value of each EDP is important. In this way, the time-history of the maximum of absolute results of ET records are plotted besides the maximum EDP from real earthquakes. To obtain an ET acceleration function by these features, it is formulated as an unconstrained optimization problem in the time domain as Eq. (5) where represents the ET acceleration function being sought, and α stands for an optimization weighting parameter set to 1.0 in this study. and are the target and displacement response for period T at time t. It should be mentioned that numerous studies have focused on the ability and applicability of ET in predicting seismic performance of various types of structures. However, none has aimed at evaluation of ET methodology in capturing the response of masonry buildings by micro modeling, including the masonry infilled frames. Besides this point that makes the results of this part of the paper interesting, high computational costs of the allocated models set limitations on performing nonlinear dynamic analysis in mass scales, including IDA. As a result, utilizing ET method as a substitute for a selected set of real ground motions significantly reduces the required analysis time:
Fig. 12Linear relationship of spectrum intensity and ET time
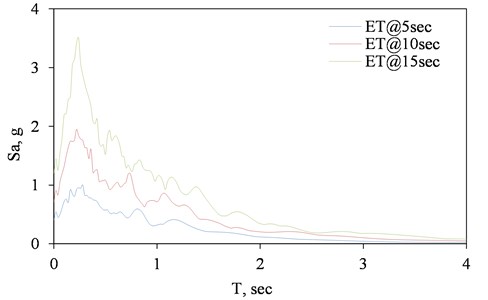
Fig. 13Schematic representation of ET records and EDP in different design levels
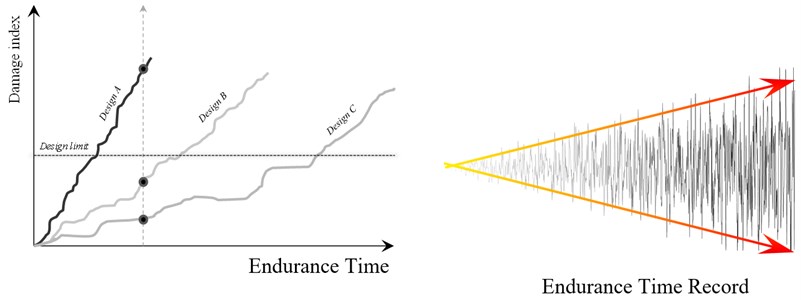
Fig. 14Method of plotting ET results
In order to determine the precision of ET method in modeling EDP of the real earthquake records, seven seismic events from among those recommended by FEMA440 [22] are taken into account. These records which are listed in Table 3, are scaled based on the codes requirements of ASCE 7-05 [23]. The mean spectrum of the seven abovementioned earthquake records as well as the design spectrum of ASCE 7-05 and the ET spectrum at 10 sec of target time are shown in Fig. 15. It is observed that there is a close convergence between these spectra which indicates the accuracy of ET in capturing the spectrum-related response of the models.
Fig. 15Comparison of codified spectral acceleration, ET’s, and the average of selected ground motions
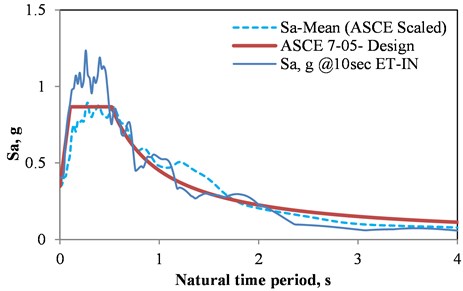
Table 3Selected earthquake records for comparative study
Date | Earthquake Name | Magnitude () | Station Number | Referred as |
06/28/92 | Landers | 7.5 | 12149 | Landers |
10/17/89 | Loma Prieta | 7.1 | 58065 | Loma-1 |
10/17/89 | Loma Prieta | 7.1 | 47006 | Loma-2 |
10/17/89 | Loma Prieta | 7.1 | 58135 | Loma-3 |
10/17/89 | Loma Prieta | 7.1 | 1652 | Loma-4 |
04/24/84 | Morgan Hill | 6.1 | 57383 | Morgan |
01/17/94 | Northridge | 6.8 | 24278 | North |
Fig. 16Comparison of variation of OP reaction force in Model-1-OP in Loma-1 and ET analyses
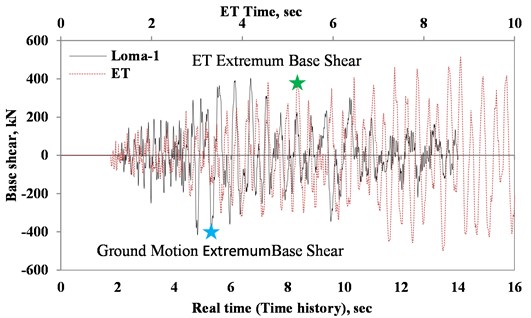
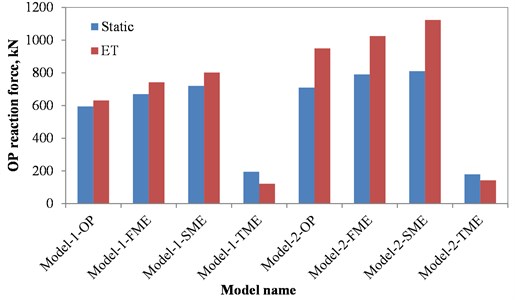
Comparison of variation of OP reaction force in Model-1-OP in Loma-1 and ET analyses is shown in Fig. 16. As can be seen, ET can capture the targeted base shear in the model with an acceptable accuracy. The results of the seven aforementioned earthquake records under incremental nonlinear dynamic analyses are compared with those of the ET in the form of OP reaction force for Model-1-OP, as shown in Fig. 17. It is obvious that the ET acceleration function can acceptably model the average results of the corresponding time history analyses; hence, used as an alternative to the time-consuming IDA. Moreover, comparison of the OP capacity of the studied models under various allocated IP demands performed by static and ET loading in OP direction is presented in Fig. 18. As it can be seen, the static loading slightly underestimates the OP capacity of the infill walls. This can be justified by the fact that the contribution of higher modes is not taken into account in static loading and therefore, in many cases, it results in underestimation of the seismic performance of buildings. In fact, when designed by nonlinear time-history analyses, a typical building is expected to benefit from some potential capacities which static analysis cannot account for. Therefore, in many cases, performing nonlinear dynamic analysis can lead to higher optimal design. However, this is not the case in models under very large IP demands; as successive OP demands in opposite directions cause reduction of OP strength for the infill walls compared to those of the corresponding static loading, as shown in Model-1-TME and Model-2-TME in Fig. 18.
Fig. 17Comparison of OP reaction force in Model-1-OP in time-history and ET analyses
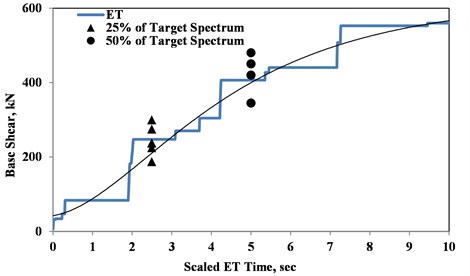
Fig. 18Comparison of static and ET in the form OP strength
5. Results discussions
The results of this study clearly indicate that up the point of IP ultimate strength (SME) for infilled frames, regardless of their aspect ratio and existence of vertical loads on the top beam and the columns, the OP strength capacity is insensitive to the IP displacement demands. However, in most cases, there is a relative increase in the OP capacity thanks to the effects of arching actions originated from formation of compressive struts in the infill walls. On the other hand, there is a sudden significant reduction in the OP strength capacity after the SME point. This is because upon the SME level, the infill wall experiences corner crushing and consequently the effects of compressive struts diminish. As a result, the arching action decreases dramatically and so does the OP strength capacity. For comparison purposes, the relation found in ASCE 41 [19] for determination of the OP capacity of infilled frames has been reported here (Eq. (3)):
where is the slenderness parameter which is 0.04 in this study, and are infill wall’s height and thickness, respectively. According to this relation, the strength capacity for Model-1 and Model-2 is 103 kN and 52 kN, respectively which is considerably lower than the results of numerical simulation. This is mainly due to fact that the aforementioned relation considers one-way arching action only; while for the assumed infilled frames, the two-way bending mechanism governs the OP behavior and therefore significant performance improvement is achieved. This improvement is even higher in Model-2 which has lower height to length ratio and consequently the two-way arching actions are more highlighted in the response of this model.
The aforementioned results can be more interesting if they are presented in the normalized form because the results are independent of some material properties and geometrical characteristics. In doing so, the normalized OP strength is defined by dividing the OP strength for each analysis to its maximum. These results for Model-1 and Model-2 are presented in Fig. 19 against the normalized IP load which is the IP force at each considered IP displacement demand level (FME, SME or TME) normalized to the IP force capacity (at SME). For comparison purposes, the results of the relation proposed by Dolatshahi et al. [24] albeit for Unreinforced Masonry (URM) walls are also presented which is a simple circle with these normalized parameters. The results obviously show that, URM infill walls benefit from arching action (the blue ellipses in the figure) prior to reaching SME level (the peak in the IP force-displacement curve) compared to URM walls. However, the reduction in the OP strength after SME level is more severe than that of the corresponding wall (the red ellipses in the figure).
Fig. 19Normalized OP strength vs. normalized IP load
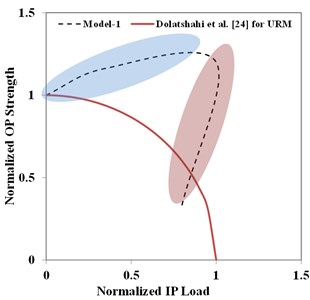
a) Model-1
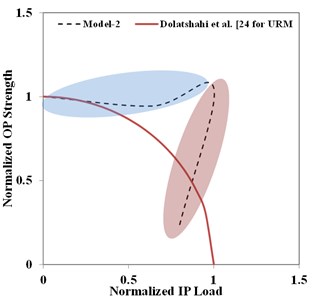
b) Model-2
Fig. 20Normalized OP strength vs. IP drift ratio
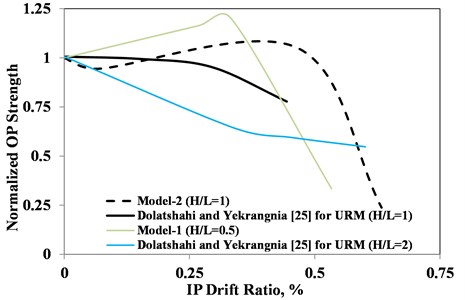
Another way of presenting IP-OP interaction for the models in this study is in the form of normalized OP strength versus IP drift ratio. These results for Model-1 and Model-2 together with the results proposed by Dolatshahi and Yekrangnia [25] are shown in Fig. 20. Although different in nature, the results of URM wall with aspect ratio of unity which are shown with black solid line are comparable with those of Model-2 as an infilled frame model with the same aspect ratio depicted with black dashed line. For comparison, the results of Model-1 with aspect ratio of 0.5 and the URM wall with aspect ratio of 2.0 are also presented. The results clearly prove that the larger the aspect ratio, the more severe the normalized OP strength reduction will be. Note that for aspect ratio of 0.5, there is an approximately 25 % increase in the normalized OP strength. However, the opposite is true for the wall with an aspect ratio of 2.0. From the results of these curves, it can be concluded that for the considered models, the IP-OP interaction can be represented by a bilinear behavior. The interesting result of these bilinear response is that the larger the slope in the first branch, the more abrupt and severe the reduction of OP strength in the second branch of these curves is.
6. Conclusions
In this paper, the in-plane (IP) and out-of-plane (OP) interaction of infilled frames having two different length-to-height ratios was studied by the use of calibrated numerical simulation. When compared to the results of nonlinear dynamic analysis, it was concluded that the static OP loading leads to accurate results in terms of OP capacity of the studied infilled frames. It was shown that regardless of the aspect ratio and existence of vertical loads, the OP behavior of infilled frames is not noticeably affected by the IP displacement demand, provided that the displacement is smaller than the displacement related to IP ultimate strength. Unlike the unreinforced masonry walls in which they experience considerable reduction in the OP strength capacity even by applying a small IP displacement [24, 25], masonry infill walls benefit from the positive effects of formation of IP diagonal compressive struts in improving the arching action as well as in increasing their OP strength capacity. This is an interesting finding in this study since it clearly proves that the IP and OP interaction for masonry infilled frames may not be much of concern and therefore, the available relations in the design codes for determination of the IP and OP strength capacity of infilled frames as independent behaviors can lead to accurate results. However, this is not the case for large IP displacement demands where the infilled frames experience severe OP strength reduction, which in turn stem from the ultimate failure mode of these structural systems i.e. corner crushing. The results of this study clearly show that although arching action in infilled frames leads to relatively higher OP strength capacities in small IP displacement demands, the resulting extra forces from this action eventually result in abrupt loss of OP strength in larger IP displacements and hence may become a matter of concern.
References
-
Pujol S., Fick D. The test of a full-scale three-story RC structure with masonry infill walls. Engineering Structures, Vol. 32, Issue 10, 2010, p. 3112-3121.
-
Tua et al. Y. H. Out-of-plane shaking table tests on unreinforced masonry panels in RC frames. Engineering Structures, Vol. 32, Issue 12, 2010, p. 3925-3935.
-
Angel R., Abrams D. Behavior of Reinforced Concrete Frames with Masonry Infill. Structural Engineering and Structural Mechanics Research Series: University of Illinois, Urbana, 1994.
-
Kuang J. S., Yuen Y. P. Effect of out-of-plane loading on in-plane behavior of unreinforced infilled RC frames. ICCCBE, Nottingham, 2010.
-
Alinejad M. Seismic Evaluation of Masonry Infill Walls in the Concrete Frame Considering In-Plane and Out-of-Plane Interaction. Tarbiat Modares University, 2011.
-
Flanagan R. D., Bennett R. M. Bidirectional behavior of structural clay tile infilled frames. Journal of Structural Engineering, ASCE, Vol. 125, Issue 3, 1999, p. 236-244.
-
Kadysiewski S., Mosalam K. M. Modeling of unreinforced masonry infill walls considering in-plane and out-of-plane interaction. PEER 2008/102, 2009.
-
Hashemi A., Mosalam K. M. Seismic evaluation of reinforced concrete buildings including effects of masonry infill walls. PEER 2007/100, 2007.
-
Abaqus. User’s Manual Version 6.9. Hibbett, Karlsson and Sorensen Inc., Pawtucket, R.I., USA, 2005.
-
Drucker D. C., Prager W. Soil mechanics and plastic analysis for limit design. Quarterly of Applied Mathematics, Vol. 10, Issue 2, 1952, p. 157-165.
-
Lubliner J., Oliver J., Oller S., Oñate E. A plastic-damage model for concrete. International Journal of Solids and Structures, Vol. 25, Issue 3, 1989, p. 299-329.
-
Kent D. C., Park R. Flexural members with confined concrete. Journal of Structural Division, Proceedings of the American Society of Civil Engineers, Vol. 97, Issue 7, 1971, p. 1969-1990.
-
Mander J. B., Priestley M. J. N., Park R. Theoretical stress-strain model for confined concrete. Journal of Structural Engineering (ASCE), Vol. 114, Issue 8, 1988, p. 1804-1825.
-
Mehrabi A. B., Benson Shing P., Schuller M. P., Noland J. L. Experimental evaluation of masonry-infilled RC frames. Journal of Structural Engineering, Vol. 122, Issue 3, 1996, p. 228-237.
-
Varela-Rivera J., Moreno-Herrera J., Lopez-Gutierrez I., Fernandez-Baqueiro L. Out-of-plane strength of confined masonry walls. Journal of Structural Engineering, Vol. 138, Issue 11, 2012, p. 1331-1341.
-
Koutromanos I., Stavridis A., Shing P. B., Willam K. Numerical modeling of masonry-infilled RC frames subjected to seismic loads. Computers and Structures, Vol. 89, Issue 11, 2011, p. 1026-1037.
-
Al-Nimry H. S. Quasi-static testing of RC infilled frames and confined stone-concrete bearing walls. Journal of Earthquake Engineering, Vol. 18, Issue 1, 2014, p. 1-23.
-
Haach V. G., Vasconcelos G., Lourenço P. B. Experimental analysis of reinforced concrete block masonry walls subjected to in-plane cyclic loading. Journal of Structural Engineering, Vol. 136, Issue 4, 2009, p. 452-462.
-
Seismic Rehabilitation of Existing Buildings (ASCE/SEI 41-06). ASCE/SEI Seismic Rehabilitation Standards Committee, American Society of Civil Engineers, Reston, VA, 2007.
-
No S. 2800-05. Iranian Code of Practice for Seismic Resistant Design of Buildings. Third Revision, Building and Housing Research Center, Iran, 2005, (in Persian).
-
Estekanchi H. E., Vafai A., Sadeghazar M. Endurance time method for seismic analysis and design of structures. Scientia Iranica, Vol. 11, Issue 4, 2004, p. 361-370.
-
Improvement of Nonlinear Static Seismic Analysis Procedures. FEMA-440. Applied Technology Council, Federal Emergency Management Agency, Washington, DC, 2005.
-
Minimum Design Load for Building and Other Structures ASCE Standard No. 007-05. American Society of Civil Engineers, Virginia, USA, 2005.
-
Dolatshahi K. M., Aref A. J., Yekrangnia M. Bidirectional behavior of unreinforced masonry walls. Earthquake Engineering and Structural Dynamics, Vol. 43, Issue 15, 2014, p. 2377-2397.
-
Dolatshahi K. M., Yekrangnia M. Out‐of‐plane strength reduction of unreinforced masonry walls because of in‐plane damages. Earthquake Engineering and Structural Dynamics, Vol. 14, Issue 13, 2015, p. 2157-2176.
