Stationary random vibration analysis of vehicle-track coupled system with nonlinear stiffness of railpads

2.1. Equation of motion of the vehicle

The metro vehicle can be modeled as a half-car system with two suspensions moving on the track. It can effectively reflect the ups and downs and nod movement of the vehicle body and front-and-rear bogies, as well as the vertical movements of four wheel sets, including 10 degrees of freedom (see Fig. 1).

Fig. 1Schematic drawings of the model of vehicle

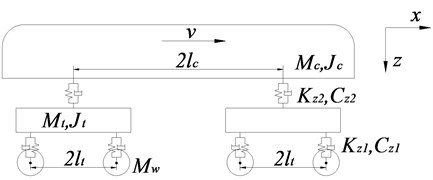
In the Fig. 1, $M_c$, $M_t$ and $M_w$ are the mass of vehicle body, bogie and wheel set; $J_c$ and $J_t$ are the rotational inertia of vehicle body and bogie; $K_{z1}$ and $K_{z2}$ are the stiffness of the first and second suspension systems, and $C_{z1}$ and $C_{z2}$ are the damping of the first and second suspension systems respectively; $l_t$ is half of the distance between two axles of same bogie; $l_c$ is half of the distance between two bogie centers; and v is the vehicle speed.

Therefore, it can be seen that the equation of motion (Eq. (1)) of the vehicle under the steady-state harmonic excitation is expressed as:

In Eq. (1), $K_v$, $C_v$, $M_v$ are the stiffness matrix, damping matrix and mass matrix of the vehicle (see Table 1), respectively; $u_v$ is the displacement vectors of the vehicle, $K_v^d$ is the dynamic stiffness matrix of the vehicle, and $f_{wr}$ is the load vector of the wheel-rail force.

2.2. Equation of motion of the track

The embedded sleeper track is the most common metro track, which can also be approximated as an infinite periodic structure (as shown in Fig. 2). Therefore, the symplectic mathematical scheme can be adopted to establish the equations of motion of the track. Where $EI$, $m_r$ is the bending stiffness and weight per meter of the rail, and $K_r$, $C_r$ is the railpad stiffness and damping.

Fig. 2Schematic drawings of vertical whole structure and substructure of embedded sleeper tracks

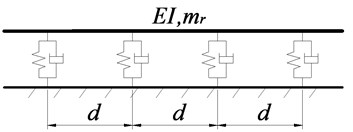
a) Whole structure

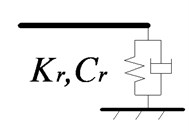
b) Substructure

2.2.1. Symplectic mathematical scheme of infinite periodic chain substructure [9]

The infinite periodic chain substructure is shown as Fig. 3.

It includes the substructure sub* under the external load $f\left(t\right)$ and the substructure sub without external load. When the substructure sub* is under a harmonic load with a specific circular frequency of $\omega$, its equations of motion can be arranged as below:

2

$\left(K+i\omega C-{\omega }^{2}M\right)\left\{\begin{array}{l}{u}_a\\ u_b\\ u_i\end{array}\right\}=\left[\begin{array}{lll}{K}_{aa}^0& K_{ab}^0& K_{ai}^0\\ K_{ba}^0& K_{bb}^0& K_{bi}^0\\ K_{ia}^0& K_{ib}^0& K_{ii}^0\end{array}\right]\left\{\begin{array}{l}{u}_a\\ u_b\\ u_i\end{array}\right\}=\left\{\begin{array}{c}{p}_a\\ -p_b\\ p_i\end{array}\right\}+\left\{\begin{array}{l}{f}_a\\ f_b\\ f_i\end{array}\right\},$

where $u_a$, and $u_b$ are the displacement vectors at the left- and right-hand interfaces and $u_i$ is the internal displacement vector and; $p_a$, $p_b$ and $p_i$ are the corresponding nodal force vectors; where $f_a$, $f_b$ and $f_i$ are the external harmonic load vectors; $K_{aa}^0$ et al. are the nine sub-blocks of the dynamic stiffness matrix.

Fig. 3Schematic drawing of infinite periodic chain structures

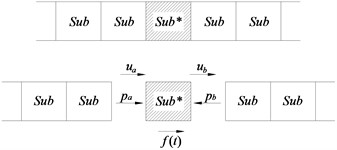
For non-loaded substructure, the internal degree of freedom in Eq. (2) can be eliminated and the following equation can thus be obtained:

3

$\left[\begin{array}{ll}{K}_{aa}& K_{ab}\\ K_{ba}& K_{bb}\end{array}\right]\left\{\begin{array}{l}{u}_a\\ u_b\end{array}\right\}=\left\{\begin{array}{c}{p}_a\\ -p_b\end{array}\right\},$

where $K_{aa}=K_{aa}^0-K_{ai}^0(K_{ii}^0{)}^{-1}{K}_{ia}^0\text{,}$$K_{ab}=K_{ab}^0-K_{ai}^0(K_{ii}^0{)}^{-1}{K}_{ib}^0\text{,}$$K_{ab}=K_{ab}^T\text{,}$ and $K_{bb}=K_{bb}^0-K_{bi}^0(K_{ii}^0{)}^{-1}{K}_{ib}^0$. Thus, Eq. (2) can be further transformed into a form of state space vector:

4

$\left\{\begin{array}{l}{u}_b\\ p_b\end{array}\right\}=S\left\{\begin{array}{l}{u}_a\\ p_a\end{array}\right\}=\left[\begin{array}{ll}{S}_{aa}& S_{ab}\\ S_{ba}& S_{bb}\end{array}\right]\left\{\begin{array}{l}{u}_a\\ p_a\end{array}\right\}=\mu \left\{\begin{array}{l}{u}_a\\ p_a\end{array}\right\},$
$S_{aa}=-K_{ab}^{-1}{K}_{aa},S_{ab}=K_{ab}^{-1},S_{ba}=-K_{ba}+K_{bb}{K}_{ab}^{-1}{K}_{aa},S_{bb}=-K_{bb}{K}_{ab}^{-1}.$

where $S$ is the wave propagation transformation matrix. $\mu$ is the propagation coefficient and eigenvalues of $S$, and so is 1/$\mu$. In addition, $\varphi$ is defined as the corresponding eigenvector. Therefore, 2$n$ eigenvectors can constitute the following matrix equation:

5

$\mathrm{\Phi }=\left[\begin{array}{llll}{\varphi }_1& {\varphi }_2& \cdots & {\varphi }_n\end{array}\right]=\left[\begin{array}{ll}{X}_a& X_b\\ N_a& N_b\end{array}\right].$

$P_a$ and $P_b$ are the dynamic stiffness matrixes of the left- and right-hand interfaces of the substructure, which can be obtained from the characteristic vector matrix $\mathrm{\Phi }$:

6

$\begin{array}{lll}{P}_a=-N_b{X}_b^{-1},& P_b=N_a{X}_a^{-1}.& \end{array}$

The degrees of freedom $u_a$ and $u_b$ in Eq. (2) be expressed in mode space as:

7

$u_a=X_{b}b,u_b=X_{a}a,$

where $a$ and $b$ are coefficient vectors. By eliminating the internal degree of freedom $u_i$ in Eq. (2), the equation about the undetermined coefficients $a$ and $b$ can be expressed as below:

8

$\left[\begin{array}{ll}{K}_{aa}^{\mathrm{*}}& K_{ab}^{\mathrm{*}}\\ K_{ba}^{\mathrm{*}}& K_{bb}^{\mathrm{*}}\end{array}\right]\left\{\begin{array}{l}b\\ a\end{array}\right\}=\left\{\begin{array}{l}{p}_{ea}\\ p_{eb}\end{array}\right\},$

where $K_{aa}^{\mathrm{*}}=\left(K_{aa}+P_a\right)X_b$, $K_{ab}^{\mathrm{*}}=K_{ab}{X}_a$, $K_{bb}^{\mathrm{*}}=\left(K_{bb}+P_b\right)X_a$, and $K_{ba}^{\mathrm{*}}=K_{ba}{X}_b$; in addition, $p_{ea}=f_a-K_{ai}^0(K_{ii}^0{)}^{-1}{f}_i$, and $p_{eb}=f_b-K_{bi}^0(K_{ii}^0{)}^{-1}{f}_i$.

After getting the vectors $a$ and $b$ through the above equation, the required responses $u_k$, $p_k$ at the $k$th interface of the periodic structure can be obtained in accordance with Eq. (9):

9a

$u_{kr}=X_a{\mu }^{k}a,p_{kr}=P_a{u}_{kr},k\ge 0,$

9b

$u_{kl}=X_b{\mu }^{-k}b,p_{kl}=-P_b{u}_{kl},k\le 0,$

where the subscripts $l$ and $r$ of $u_k$, $p_k$ mean the left- and right-hand interfaces of the substructure; positive $k$ is to the right of the loaded substructure and negative $k$ is to its left, with the zeroth interface being between the loaded substructure and the one to its right for $k>0$ and to its left for $k<0$.

2.3. Vehicle-track vertical coupled relations

Assuming that the vehicle and the track are connected through linear Hertz contact spring $k_h$ [21], the wheel-rail force can be thus expressed as:

where $u_{ri}$ is the displacement of the rail at the $i$th wheel-rail contact point, $r_i$ is the pseudo track irregularity, $u_{wi}$ is the displacement of the $i$th wheel set.

For a single carriage, there are four contact points between wheel and rail. The left- and right-hand displacement vectors of the $i$th substructure, $u_{l,i}$ and $u_{r,i}$, can be obtained as the sum of the responses caused by each of the four wheel-rail forces, i.e.:

Consequently, the displacement of the rail at the contact point is expressed as:

Further, the equation of motion of the coupled vehicle-track system can be obtained:

where $\stackrel{-}{K}$is the dynamic stiffness matrix of the coupled system, $\stackrel{-}{U}={\left\{u_v,b_1,a_1,b_2,a_2,b_3,a_3,b_4,a_4\right\}}^T$, and $\stackrel{-}{F}$ is the pseudo force vector.

2.4. Pseudo-excitation method for random vibration of the vehicle-track coupled system

Pseudo-excitation method is an accurate and efficient random vibration analysis method. The stationary random vibration analysis can be equivalent to the harmonic vibration analysis.

(a) $S_{xx}\to H\left(\omega \right)\to S_{uu}={\left|H\right|}^2{S}_{xx}$,

(b) $x=e^{i\omega t}\to H\left(\omega \right)\to u=H{e}^{\omega t}$,

(c) $\tilde{x}=\sqrt{S_{xx}}{e}^{i\omega t}\to H\left(\omega \right)\to \tilde{u}=\sqrt{S_{xx}}H{e}^{i\omega t}$.

Basic principle of pseudo-excitation method is shown in Fig. 4. According to the traditional random vibration theories, when the linear system is subjected to the single-point stationary random excitation of the PSD $S_{xx}$, the response PSD of the system $S_{uu}$ is shown in Fig. 4(a); if the system is subjected to the unit harmonic load $e^{i\omega t}$, its corresponding response will be shown in Fig. 4(b); According to the nature of linear system, if $\sqrt{S_{xx}}$ is multiplied by the unit harmonic load $e^{i\omega t}$, its response should also be multiplied by $\sqrt{S_{xx}}$, as shown in Fig. 4(c). Thus, the pseudo excitation $\sqrt{S_{xx}}{e}^{i\omega t}$ can be constructed, and the pseudo response $\tilde{u}$ can be obtained. In this way, the response PSD can be acquired by multiplying pseudo response with its complex conjugate:

Based on the pseudo-excitation method, we can know that if the PSD of the track irregularity $S_r\left(\omega \right)$ is known, the pseudo-excitation vectors of the single carriage at the four vehicle-track contact points can be constructed:

where $t_2=\left(2l_t\right)/v$, $t_3=\left(2l_c\right)/v$, and $t_4=2(l_t+l_c)/v$; $v$ is the vehicle speed. After the pseudo-excitation is introduced, the pseudo force vector $\stackrel{-}{F}$ of the vehicle-track coupled system can be expressed as:

Thus, the pseudo response $\tilde{u}$ of the vehicle-track coupled system can be obtained, and the PSD of the response $u$ can be solved by means of Eq. (17).

3.1. The main calculation parameters

By using the above symplectic model established for the random vibration of the vehicle-track coupled system，taking the type-B metro vehicle running on the embedded sleeper ballast less track with the American fifth-grade vertical irregularity PSD (with a wavelength longer than 1 m) and the track irregularity PSD of Chinese Shi-tai line (with a wavelength less than 1 m) at the speed of 80 km/h as a subject for study, the impact of the frequency-dependent stiffness of rail pads on the vertical random vibration response of the vehicle body, bogie, wheels and rail in frequency domain is explored. The calculation parameters of the type-B metro vehicle and the embedded sleeper ballast less track are shown in Table 1 and Table 2.

3.2. The measurement and prediction of the dynamic mechanical performances of rail pads

As far as most of high polymer materials are concerned, the similar dynamic mechanical performances can be observed at low temperatures or high frequencies. According to Time-Temperature Superposition (TTS) and WLF formula, the temperature-dependent and frequency-dependent dynamic mechanical parameters of rail pads can be predicted based on the experimental results at a certain frequency and under the different temperatures.

3.2.2. Experimental parameters

In this test, the full-size rail pads of WJ-7 fasteners which was often used in China’ high-speed railway, the universal testing machine equipped with a temperature control box, a section of steel rail (60 kg/m), several emery cloths, a loading steel plate and two supporting steel plates (Fig. 5).

In view of China’s high-speed vehicle’s dynamic weight of 8×85 kN (increasing by 10 % than its actual static weight), the preload of two springs in a fastener (generally, about 20 kN) and the load-sharing scale of a fastener (generally, 0.4-0.6), the exciting dynamic loads on a rail pad should reciprocate between 20 kN and 70 kN. For safety’s sake, the periodic dynamic force-displacement curves of the test rail pads were measured at a certain frequency of 0.3 Hz and under the different temperature points of –60-+20 °C with an interval of 2.5 °C. The periodic dynamic force-displacement curves of WJ-7 rail pads at 0.3 Hz and under –30 and +20 °C are shown in Fig. 6.

Fig. 5a) Universal testing machine equipped with a temperature control box in which the dynamic mechanical parameters of the soft pads in b) WJ-7 fasteners are measured under –60-+20 °C

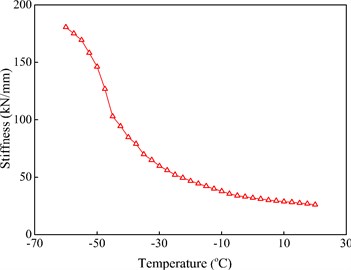
According to periodic dynamic force-displacement curves of linear viscoelastic materials, the stiffness of the soft pads in WJ-7 fasteners can be obtained at 0.3 Hz and under the temperatures of –60-+20 °C with an interval of 2.5 °C, as shown in Fig. 7.

Fig. 6The periodic dynamic force-displacement curves of WJ-7 rail pads at 0.3 Hz and under 20 °C

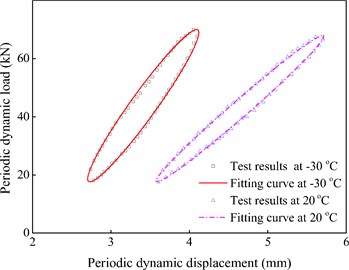
Fig. 7The stiffness of WJ-7 rail pad at 0.3 Hz and under the temperatures of –60-+20 °C

3.2.3. Prediction of the untested dynamic mechanical performances of rail pads

Since the dominant frequencies of the environment vibrations due to high-speed railway are low, only the stiffness of the soft pads in WJ-7 fasteners within 1000 Hz are predicted under the temperatures of –60-+20 °C.

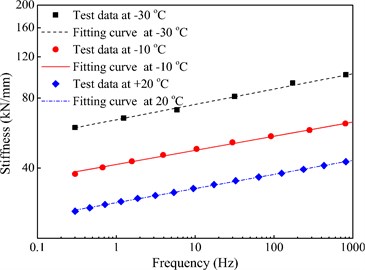
Fig. 8 shows the frequency-dependent stiffness of the test pads in WJ-7 fasteners within 1000 Hz and under –30, –10 and +20 °C. It is clear that the actual dynamic mechanical parameters of rail pads are not supposed to be the frequency-independent and temperature-independent constants. Overall, the stiffness of rail pads increase with the decrease of temperatures or the increase of frequencies.

It can be found that the stiffness of rail pad of different kinds of high polymer materials and the excitation frequency approximately form a linear relationship under the logarithmic coordinate system [23-25], as expressed in Eq. (27):

27

${\mathrm{l}\mathrm{o}\mathrm{g}}_{10}^K=k\times \left({\mathrm{l}\mathrm{o}\mathrm{g}}_{10}^f-{\mathrm{l}\mathrm{o}\mathrm{g}}_{10}^{f_0}+{\mathrm{l}\mathrm{o}\mathrm{g}}_{10}^{K_0}\right),$

where $K_0$ is the low-frequency initial stiffness of the rail pad at the low excitation frequency $f_0$ (usually $f_0=$ 3-5 Hz); $k$ is the slope of the linear relationship between the rail pad stiffness and excitation frequency under the logarithmic coordinate system, representing the frequency-dependent extent (or frequent-dependent degree) of the rail pad stiffness. It can be easily seen from Eq. (27) that the relationship between the stiffness of rail pad of different materials and the excitation frequency mainly depends on its low-frequency initial stiffness $K_0$ and its stiffness' frequency-dependent extent $k$.

According to the experimental data, the linear slope for the changes in the stiffness of WJ-7 rail pad with the frequency under the logarithmic coordinate system is all 0.07 under –30, –10 and +20 °C; in addition, the initial stiffness of WJ-7 rail pad is 31.0, 45.2 and 70.8 kN/mm under an excitation of 3-5 Hz.

Fig. 8The frequency-dependent stiffness of WJ-7 rail pad within 100 Hz and under –30, –10 and +20 °C

3.3. The impact of the rail pad frequency-dependent stiffness on the random vibration response of the coupled vehicle-track system

The comparison of impact the rail pad frequency-dependent stiffness and constant stiffness on the random vibration response of the coupled vehicle-track system at the temperature of 20 °C was presented. The vertical random vibration acceleration of the vehicle body, bogie, wheelset and rail under these two calculation conditions are shown in Fig. 9-12.

Fig. 9 shows the PSD of the vertical random vibration acceleration of the vehicle body under the rail pad constant stiffness and frequency-dependent stiffness. It can be seen from Fig. 9 that the calculation results under the two calculation conditions basically overlap. This result suggests that the impact of the rail pad frequency-dependent stiffness on the vertical random vibration response of the vehicle body can be neglected.

Fig. 10 presents the PSD of the vertical random vibration acceleration of the bogie under the rail pad constant stiffness and frequency-dependent stiffness. It can be seen from Fig. 10 that the calculation results under the two calculation conditions have very little difference within 15 Hz. By reading the PSD peak value at 7.02 Hz, we can know that there is only a small gap of 2.0×10^-6 m²/s⁴/ Hz between these two conditions, as shown in Fig. 10(a). However, as the frequency varies within 20-100 Hz, there is a huge difference between them, as shown in Fig. 10(b). For example, when the frequency varies within 20-45 Hz, given that the calculation condition of the frequency-dependent stiffness of rail pads has a small calculation value, namely, the calculation result under the rail pad frequency-dependent stiffness is 88.5 % of that under the rail pad constant stiffness at Point A in Fig. 10(b); yet, with the frequency range of 45-100 Hz, the calculation result under the constant stiffness condition is small, namely, the calculation result under the rail pad constant stiffness is only 56.1 % of that under the rail pad frequency-dependent stiffness at Point B in Fig. 10(b). Thus, it is not hard to find that the calculation result without considering the frequency-dependent stiffness of the rail pads will not only underestimate the vibration of the bogie within the frequency range of 45-100 Hz but also overestimate the vibration with the frequency range of 20-45 Hz. In other words, the rail pad characteristic of the frequency-dependent stiffness changes the distribution of the random vibration of the bogie in the frequency domain.

Fig. 9PSD of vertical random vibration acceleration of the vehicle body

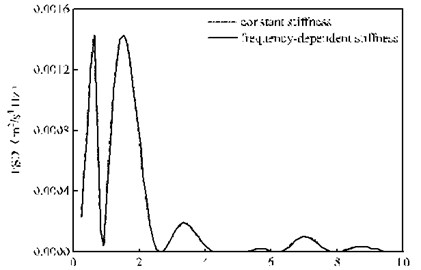
Fig. 10PSD of the vertical random vibration acceleration of the bogie

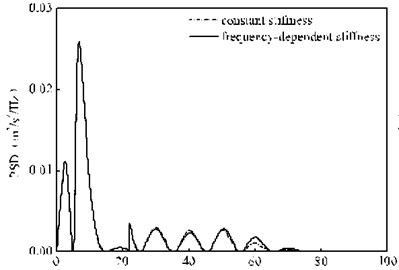
a) 0-100 Hz

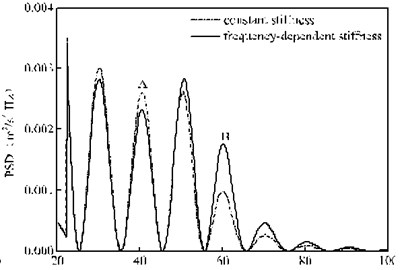
b) 20-100 Hz

Fig. 11 shows the PSD of the vertical random vibration acceleration of the wheelset under two different calculation conditions. It can be seen that, the frequency-domain random vibration acceleration of the wheelsets mainly concentrate within the range of 30-100 Hz. In addition, it can be seen from Fig. 11 that, compared with the calculation condition of rail pad constant stiffness, the frequency-dependent stiffness not only significantly increases the vertical random vibration acceleration of the wheelset within the frequency range of 50-200 Hz, but also enhances the 1st dominant frequency. Fig. 11 suggests that, when the rail pad stiffness is constant, the highest PSD peak of the vertical random vibration acceleration of the wheelset reaches 8.82 m²/s⁴/Hz and corresponds to the 1st dominant frequency of 47.9 Hz; when the rail pad stiffness is frequency-dependent, the highest PSD peak of the vertical random vibration acceleration of the wheelset rises to 13.5 m²/s⁴/Hz and its corresponding 1st dominant frequency also increases to 57.1 Hz. To sum up, the frequency-dependent stiffness of rail pad alters not only the frequency-domain amplitudes of the vibration but also its frequency-distribution at center frequencies higher than 30 Hz. The random vibration of the wheel is transferred to the high frequency in the frequency domain.

Fig. 12(a) shows that in the range of 0-100 Hz, the effect of frequency-dependent rigidity on the random vibration of the rail is basically the same as that of the wheelset, that is, the frequency-dependent stiffness of rail pads clearly decreases the random vibration of rail below 50 Hz, and significantly increases the random vibration of rail above 50 Hz. In the frequency range of 100-1000 Hz, the PSD peak fluctuation of the rail vibration acceleration power spectrum is very severe, which is caused by the periodic vibration of the rail due to the fixed wheelbase according to the existing research [26]. There is a peak at 840 Hz, which is mainly due to the self-vibration characteristics of the rails, on the overall trend of the rail acceleration PSD. Fig. 12(b) shows that every two adjacent peaks of the rail vibration acceleration PSD between the frequency interval $f_{int}$ is equal to $v/l$ (10 Hz), where $v$ is the vehicle speed, $l$ is a fixed wheelbase. In addition, the influence of frequency-dependent stiffness on the response of the rail vibration acceleration becomes very small in this frequency domain, and the difference between the two cases is only 1 %. The random vibration curve of the rail is the shape of the wave mainly due to two reasons which are due to the periodic vibration caused by the fixed wheelbase of the vehicle body and the free-vibration characteristic of the track structure itself.

Fig. 11PSD of the vertical random vibration acceleration of the 2nd wheelset

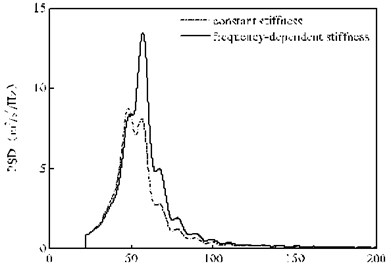
Fig. 12PSD of the acceleration of the rail the under the 2nd wheelset

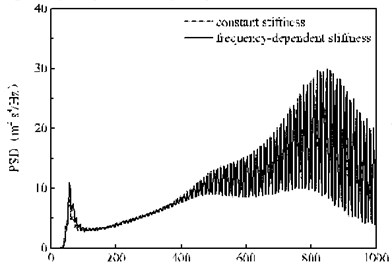
a) 0-1000 Hz

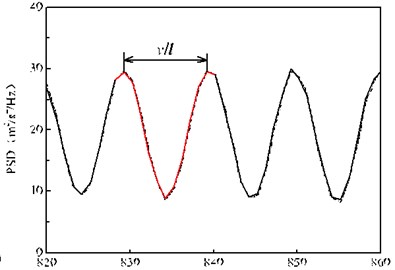
b) 820-860 Hz

3.4. The impact of the environment temperature on the random vibration response of the coupled vehicle-track system

The experimental results show that the stiffness of the fastener is not only affected by the excitation frequency, but also has a great relationship with the environment temperature. In this section, we will study the influence of the frequency-dependent and temperature-dependent stiffness of the rail pads on the random vibration of the vehicle-track coupled system. In this analysis, the frequency-dependent extent $k$ of the rail pads stiffness is taken as 0.07 and the environment temperature is considered as –30, –10 and 20 °C.

Fig. 13 shows the random response of the vehicle body under three temperature conditions. The calculated results are in good agreement with each other, indicating that the impact of the rail pads temperature-dependent stiffness on the response of the vehicle body is negligible.

Fig. 14 shows the random vibration acceleration response spectrum of the bogie at three temperatures. Fig. 14(a) can be seen that the calculation results of the three conditions in the 0-20 Hz range is basically the same, but the difference in the 20-100 Hz range is obvious. Fig. 14(b) shows that at the peak A position, the bogie acceleration response PSD peak at the three ambient temperatures (–30, –10 and 20 °C) is 4.51×10^-3 m²/s⁴/Hz, 1.78×10^-3 m²/s⁴/Hz and 4.60×10^-4 m²/s⁴/Hz, respectively corresponding to the dominant frequency of 71.2 Hz, 70.0 Hz and 70.0 Hz. In summary, the temperature-dependent stiffness of the rail pads only affects the amplitude of the PSD in the frequency domain above 20 Hz, and the influence on the main frequency is relatively small. With the frequency of 63 Hz as the critical position, when the frequency is less than 63 Hz, the higher the temperature, the PSD peak of the bogie random vibration acceleration greater, but when the frequency is more than 63 Hz, the conclusion is just the opposite. It indicates that the law of the temperature-dependent stiffness of the rail pads on the random vibration of the bogie is different in different frequency bands.

Fig. 13PSD of vertical random vibration acceleration of the vehicle body

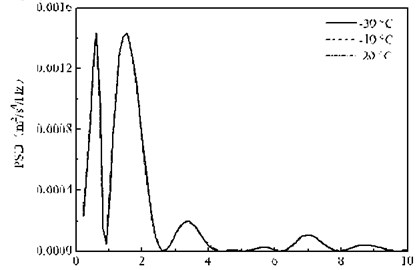
Fig. 14PSD of the vertical random vibration acceleration of the bogie

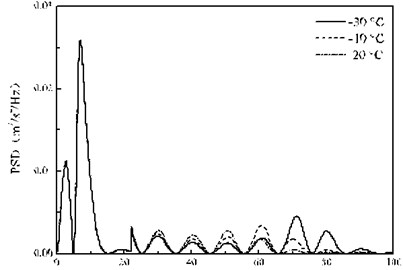
a) 0-100 Hz

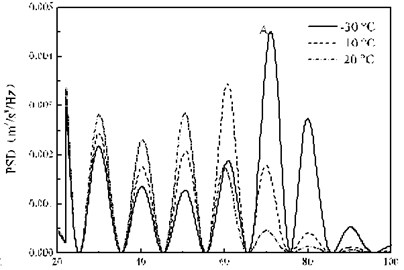
b) 20-100 Hz

Fig. 15 shows the results of the wheelset acceleration PSD under three ambient temperatures. It is not difficult to find that the temperature variation stiffness of the fastener has great influence on the wheel acceleration response, including the peak value and the corresponding dominant frequency. The PSD peak of the wheelset acceleration response is 63.4 m²/s⁴/Hz, 27.5 m²/s⁴/Hz and 13.1 m²/s⁴/Hz respectively, and the corresponding dominant frequencies are 73.4 Hz, 63.1 Hz and 50.3 Hz. The lower the temperature, the greater the peak value of the wheelset acceleration PSD and the higher the corresponding dominant frequency, and this change was a nonlinear increase in the trend. This is because the rail pads stiffness decreases gradually with the temperature, making the resonance frequency of the wheel-rail coupled system increases, so that the energy of wheel random vibration transfer to the high-frequency domain. As the temperature increases linearly, the increasing trend of the peak value of the random vibration acceleration PSD of the wheel is nonlinear.

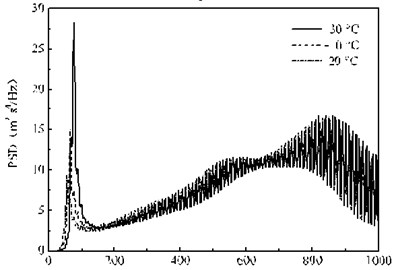
Fig. 16 shows the random vibration PSD of the rail under three temperatures. The influence of the rail pads temperature-dependent stiffness on the rail acceleration is the same in the range of 0-200 Hz, and the effect of temperature on the rail acceleration response is gradually reduced in 200-600 Hz. The difference between the three temperature conditions is stable above 600 Hz, and the difference is less than 5 %. It is shown that the rail pads temperature-dependent stiffness only affects the rail acceleration within 200 Hz, but less on the high frequency vibration above 200 Hz. Because the fastener is in direct contact with the rail, the stiffness of the fastener pad has a certain influence on the whole frequency domain of the rail, and the influence law is complicated and nonlinear.

Fig. 15PSD of the 2nd wheelset acceleration

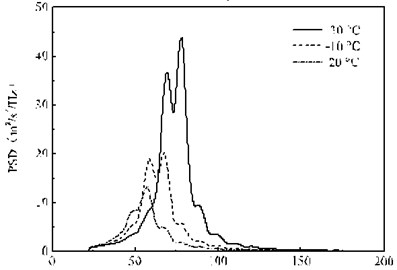
Fig. 16PSD of the acceleration of the rail under the 2nd wheelset

With the comparison of Fig. 11 and Fig. 15, considering the range of environment temperature and the frequency-dependent extent of the rail pads of WJ-7 fastener, the PSD peak of the vertical random vibration acceleration of the wheelsets gets the maximal increase of 3.3 times at least, and its 1st dominant frequency has the biggest increment of 20.6 Hz or more. Therefore, in order to accurately analyze the random vibration responses of the vehicle-track coupled system, experiments must be conducted to obtain the accurate kinetic parameters of the polymer materials like rail pads.