Analysis on vibration response of structure of hydrocyclone under action of internal spiral flow

2.1. The geometric model and fluid parameter

The variable diameter circular pipe structure of hydrocyclone whose main diameter is 28 mm is selected as the research object. The length of tail pipe part is 570 mm, the large cone angle and small cone angle are 20 degrees and 1.5 degrees respectively. The model consists of fluid domain and solid domain. The material of solid domain is organic glass, the wall thickness of organic glass tube is 5.5 mm, the density is 1.18×10³ kg/m³, modulus of elasticity is 3×10⁹Pa, and the Poisson’s ratio is 0.347. The fluid domain uses water as the flow medium, the density is 998.2 kg/m³, the viscosity of water is 1.0 mPa s. When the structure is working, both ends of the pipe are fixed. The vibration of the variable diameter circular tube structure under the internal fluid pulsation is considered. And the spiral turbulence in the same pipe constitutes a FSI system. Its mechanical model is shown in Fig. 1.

Fig. 1The fluid structure interaction mechanics model of variable diameter pipe

2.2. FSI calculation model and method

In the fluid microelectronics of the hydrocyclone, the mass conservation and the conservation of momentum should be satisfied.

Governing equations for the fluid part.

The continuous equation is:

The momentum conservation equation is:

Governing equations for the solid part.

The balance equation is:

Dynamic equation is:

Fluid-structure interaction interface equation is:

where, the temperature change of the fluid in the hydrocyclone is not considered, and at the interface of fluid domain and solid domain, the force and the displacement are equal.

Where, $a_s$ is a local acceleration vector in the solid domain (m/s²); $f_f$ and $f_s$ are volume force vector of fluid and solid (N), respectively; ${\rho }_f$ and ${\rho }_s$ are density of fluid and solid (Kg/m³), respectively; $u$ is velocity vector of fluid (m/s); ${\sigma }_s$ is cauchy stress tensor (N); $\left[M\right]$, $\left[C\right]$ and $\left[K\right]$ are mass matrix, damping matrix and stiffness matrix, respectively; $\left\{F_f\right\}$ is the load of the fluid to the structure; ${\tau }_f$, ${\tau }_s$ are interface stress of fluid and solid (N), respectively; $s_f$ and $s_s^{}$ are interface displacement of fluid and solid (m), respectively.

The numerical simulation applies the Ansys FEM and the Fluent platform. Based on the small deformation assumption, the finite volume method is adopted in the fluid domain, and the RSM model is adopted in the turbulent model for the flow field computation. The ALE method is adopted in the dynamic mesh. The finite element theory is applied in the solid domain, and the New-mark time integral method is used to solve the dynamic equation of the variable diameter circular tube structure of a hydrocyclone. And the calculation method of interlaced iterative coupling solution is adopted to realize the two-way coupling numerical calculation of the variable diameter circular tube of a hydrocyclone. The inlet of the hydrocyclone adopts velocity entrance boundary (m/s), and the underflow outlet and the overflow outlet both use the full development of boundary condition.

2.3. Two-way fluid-structure coupling iteration method

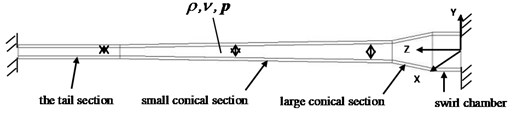
The interaction between fluid and structure is considered, that is, the effect of fluid pressure change on the distribution of structural stress and displacement, and the disturbance of the structure vibration to the internal fluid will also affect the distribution of the fluid pressure. The relation between the interfacial force of the structure and displacement transfer of the variable diameter circular pipe fluid is shown in Fig. 2.

Fig. 2Force and displacement transitive relation at coupling interface

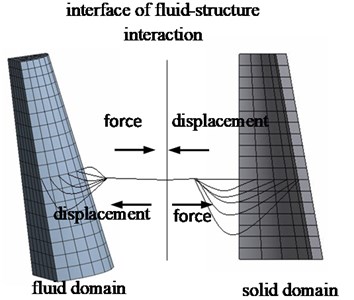
Fig. 3Two-way FSI solution iterative process

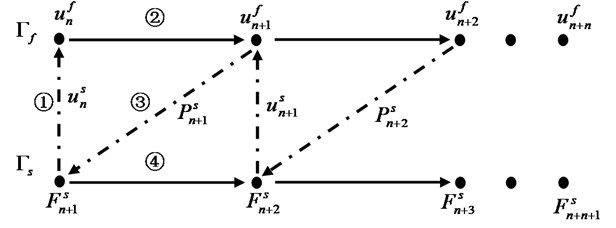
The calculation method and interface equation of fluid domain and structure domain are established respectively. To achieve two-way coupling calculation of variable diameter pipe of hydrocyclone, it depends on iterative calculation method. The characteristics are that the fluid domain and the structure domain are integrated in time domain by the application of their respective solution methods, and the response of the FSI is promoted in a time interlaced way. In this way, the fluid domain and the solid domain can be calculated by different operators, such as the finite volume method in the fluid domain, and the finite element method in the solid domain. The flowchart of the interlaced iteration is shown in Fig. 3.

3.1. Analysis of structure deformation under coupling action

Figs. 4-6 are the equivalent deformation diagrams of the variable diameter circular tube structure of the hydrocyclone under coupling action, when the inlet velocity is 6.8 m/s, 8.2 m/s and 10.2 m/s respectively. As can be seen from the figure, the maximum deformation position of the structure is back-end of the small conical section, namely junction of small conical section and the tail section. With the increase of the inlet velocity, the maximum deformation value of hydrocyclone is increasing, and the maximum deformation values of three kinds of inlet velocity are 0.007456 mm, 0.28915 mm and 0.45705 mm, respectively. When the inlet velocity is 6.8 m/s, the influence on the structural deformation is very small. Compared with the inlet velocity 8.2 m/s and 10.2 m/s, the difference is nearly two orders of magnitude, which indicates that the influence on the deformation of the structure is becoming more significant when the inlet velocity is greater than 8.2 m/s.

Fig. 4Structural displacement diagram at 6.8 m/s

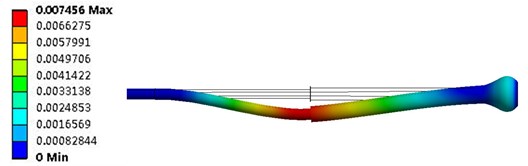
Fig. 5Structural displacement diagram at 8.2 m/s

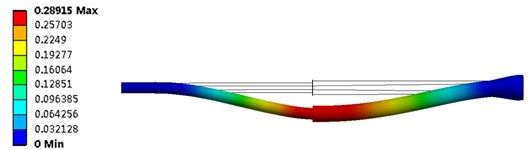
Fig. 6Structural displacement diagram at 10.2 m/s

3.2. Interfacial stress distribution under coupling action

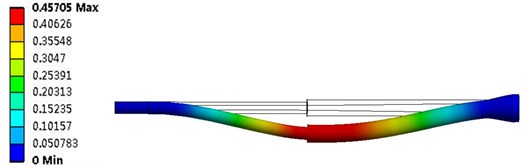
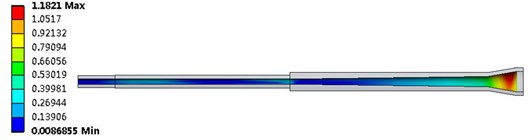
Figs. 7-9 is the equivalent stress distribution cloud diagram at the interface between the fluid and the structure of a hydrocyclone’s variable diameter circular tube under three kinds of inlet velocity. As can be seen from the diagrams, the maximum stress position of the structure is mainly concentrated in the large cone-shaped part. With the increase of the inlet velocity, the stress is increasing, and the maximum stress values corresponding to the three kinds of inlet velocity are 0.34 MPa, 0.77 MPa and 1.18 MPa respectively. It can also be seen that the stress is not symmetrical at the interface, and the greater the inlet velocity is, the more obvious the asymmetry is. And in the high inlet velocity, there is also a asymmetric relatively large stress distribution in the intersection of the small cone and the tail pipe. These phenomena indicate that the coupling of fluid and structure has an influence on the distribution of forces on the structure.

Figs. 7-9 are the equivalent stress distribution diagram at the interface between the fluid domain and the solid domain in the hydrocyclone under three kinds of inlet velocity. From the graph, we can see that the location of the maximum stress is mainly concentrated in the large conical section. With the increase of the inlet velocity, the maximum stress value of hydrocyclone is increasing. The maximum stress values of the three kinds of inlet velocity are 0.34 MPa, 0.77 MPa and 1.18 MPa respectively. At the same time, we can also see that the stress at the interface are not symmetrical, with the inlet velocity greater, the asymmetry is more obvious, and at high inlet velocity, there are bigger stress distribution at junction of small conical section and the tail section. These phenomena indicate that it has an impact on the distribution of forces in the structure under FSI.

Fig. 7The interface stress distribution of fluid and structure at 6.8 m/s

Fig. 8The interface stress distribution of fluid and structure at 8.2 m/s

Fig. 9The interface stress distribution of fluid and structure at 10.2 m/s

3.3. Comparative analysis of measured data and simulated data

The test instrument applies the 24 channel SCADAS Mobile data acquisition system of Belgium LMS company, and LMS Test.Lab testing and analysis software is used. Fig. 10 is a hydrocyclone entity for experimental test. The piezoelectric sensor is directly installed on the variable diameter pipe of the hydrocyclone. The sensor uses PCB company’s ICP accelerometer, and the sensitivity is 100 mV/g and 1000 mV/g, respectively, two types. The sampling frequency range is 0-500 Hz, and the frequency resolution precision is 0.5 Hz. After the data acquisition analyzer is processed, the display shows the vibration waveform as shown in Fig. 11.

Fig. 10Entity structure of hydrocyclone

Fig. 11Signal gathering analytical instruments

Fig. 12Original time domain signal

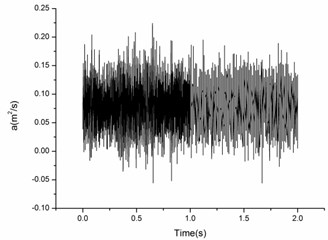
Fig. 13amplitude frequency curve when velocity is 10.20 m/s

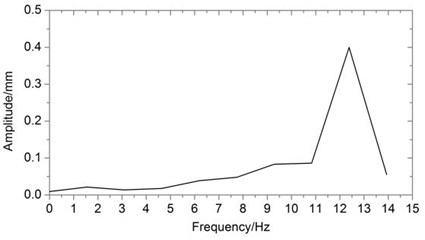
Fig. 12 shows original time domain signal of position 2 at inlet velocity of 8.2 m/s, and the value of the maximum acceleration is about 2.3 m²/s. Fig. 13 shows the amplitude frequency curve of the structure subjected to the impact of the fluid, when the inlet velocity is 10.2 m/s. The vibration frequency of the structure is increasing with the flow velocity increases. Through the amplitude frequency curve, the excitation frequencies of the three kinds of inlet velocities are 0.511 Hz, 2.01 Hz and 12.38 Hz respectively. Modal analysis has obtained that the natural frequency of low order structure under working condition is about 36 Hz, and with the inlet velocity increases, the natural frequency is decreased, and the structure vibration frequency under the action of fluid is increasing with the flowrate increases, if the inlet velocity of fluid flow is too large, it will cause the resonance of the structure, which is need to pay attention to in the actual the problem.

(1) Measuring-point arrangement.

Ten measuring points are arranged on the variable diameter circular tube of the hydrocyclone, and the position of the measuring points is shown in Fig. 14. Because the geometric model is symmetrical around the circle, the structure is simplified into rods. The positions are measured at the horizontal axis ($X$ axis) and the vertical axis ($Y$ axis) of the same axis section position. The final result of the average data of ten measurements is taken.

(2) Comparison and analysis.

Table 1 gives the absolute values of the maximum acceleration of each measurement point at $X$ axis direction and $Y$ axis direction. The T and S represent the measured data, and the numerical simulation data respectively.

1) In both axial directions, the variation trend of values of the maximum acceleration at different inlet velocities is similar. Namely, the acceleration values at position 1 and position 10 near the fixed constraint are smaller, while the acceleration value is larger in the middle area, similar to the parabolic form, which reflects the first order vibration mode of the structure.

Fig. 14Measuring point distribution of hydrocyclone

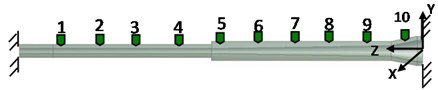
2) The measured values at both ends are generally greater than the simulated values, while those in the central region are lower than the simulated values. This is mainly due to the difference between the boundary conditions of the simulated and the measured. At the time of simulation, the both ends are fixed constraints. However, due to the manufacturing and installation errors and the fluid load, there is a slight displacement at the two ends of the structure at the time of measuring.

3) With the increase of the inlet velocity, the differences between the measured data and the numerical simulation data increases slightly. But the variation trend between simulated and the measured is consistent. In addition to positions of both ends, the maximum response values of measured and simulated points are in agreement, indicating that the established FSI model is reasonable.