Repetitive impacts recovering using variational mode extraction with constructed reference enhanced by improved blind deconvolution

1. Introduction

State monitoring and fault diagnosis of rotating machinery based on vibration signals has become the mainstream. However, the collected vibration signal of faulty rotating machinery is essential one kind of multi-source signal, and its fault features are often very weak due to the long signal acquisition path and the interference of other signal components. Normally, the signal needs to be filtered or decomposed into several sub-signals, then the feature extraction method is performed on the filtered signal or some sub-signals to obtain an accurate diagnosis conclusion. Various methods have been proposed to meet the above requirement such as wavelet transform [1], followed by the sparse representation analysis method based on predefined dictionary [2-3]. However, the decomposition quality of wavelet transform has a great relationship with the selected wavelet basis. So far, the construction or selection of wavelet basis has not been resolved perfectly. Though the sparse representation analysis method based on predefined dictionary, also naming as analytical dictionary [4-7] solves the problem of wavelet basis selection to certain extent, it has the defects of requiring much more prior knowledge of the analyzed signal. Sparse representation analysis method based on self-learning dictionary [8-11] does not require prior knowledge of the analyzed signal, and the optimal dictionary set could be learned adaptively based on the analyzed signal, but its huge amount of calculation and low computational efficiency limit its engineering application. Empirical mode decomposition (EMD) is a decomposition method for non-stationary signal, and it could decompose the multicomponent signal into a series of intrinsic mode functions (IMFs) to achieve better feature extraction result. However, its inherent mode aliasing and weak mathematical theory limit its further popularization and application [12]. Besides, EMD is extremely susceptible to noise interference since its algorithm is based on the local maximum expansion [13]. In recent years, although various of EMD improved methods have solved the above-mentioned shortcomings of EMD to some extent [14-15], most of them have the disadvantage of a large amount of calculation.

As a variational, non-recursive, multi-resolution decomposition method, variational mode decomposition (VMD) has higher computational efficiency and stronger noise robustness than EMD, and it has achieved certain applications in the area of fault diagnosis [16-18]. VME only extracts the target signal, but VMD will decompose the analyzed signal into a series of signals at the same time, so unnecessary extra calculation will be generated. In addition, the number of decomposition modes needs to be predetermined for VMD, and the number choice of decomposition modes will produce great contingency on the decomposition results. So far, there is still no relevant literature to solve the problem perfectly. VME being derived from VMD has the same calculation concept as VMD: Wiener filtering, Hilbert transform and variation [19], and it could use prior knowledge of the analyzed signal to extract the specific pattern being buried in the analyzed signal. Furthermore, the calculation efficiency of VME could be improved greatly compared with VMD due to the reason that it only extracts the specific pattern hidden in the analyzed signal. However, the extraction effect of VME often depends on whether the feature of the target extracted component being buried in the analyzed signal is obvious or not. As mentioned above, the impulse characteristic of rotating machinery’ vibration signal is often weak owing to the signal attenuation of the signal acquisition path, and the analyzed signal needs to be preprocessed to enhance the impulse characteristic before applying VME on the analyzed signal. Minimum entropy de-convolution (MED) [20] is often used as a preprocessing method for the enhancement of impulse characteristic, and the characteristic of traditional MED is that it will use the maximize kurtosis of its output as the termination condition. Endo et al. used MED for impact fault signal extraction of rotating machinery for the first time [21], then MED and its related algorithms have been used widely in the area of fault diagnosis [22-24]. However, the following two problems of MED still need to be solved to obtain much better extraction effect: (1) the theoretical goal of MED is to filter out a few obvious impulsive components hidden in the background noise through the de-convolution optimal filter. However, it is often hoped to extract an impact component in each fault cycle. (2) Additional impact components at signal discontinuities also might be de-convoluted by MED, which may lead to misjudgment results. MCKD [23] algorithm de-convolutes the impulse signal based on the prior knowledge of the failure rotating machinery. The above-mentioned two shortcomings of MED could be solved by MCKD to some extent. However, MCKD has the following problems in engineering applications: (1) Prior knowledge of the fault cycle is required. (2) Resampling is required when the fault cycle is irregular. (3) Its calculation efficiency is lower compared with MED. (4) MCKD cannot extract impact fault signals effectively when the background noise is strong. Aiming at solving the above-mentioned related drawbacks of MED and MCKD, an IMED method is proposed, which uses a time target vector to define the impact position determined by MED. The proposed method does not need to construct an optimal filter iteratively same as MED, and it also does not need the prior knowledge such as the failure cycle of rotating machinery same as MCKD. In addition, the proposed method has stronger noise robustness than the above two methods, and it could extract the early weak fault features of rotating machinery effectively.

Based on the above stated, an effective fault feature extraction method named as repetitive impacts recovering using VME with constructed reference enhanced by IMED is proposed. The proposed method combines both the advantages of IMED in solving the influence of the long signal acquisition path and VME based on constructed reference in extracting the impulse and modulation characteristic of vibration signal. Firstly, IMED is used as signal preprocessing method to analyze the vibration signal of rotating machinery to eliminate the influence of the signal acquisition path. Meanwhile, the repetitive impulse characteristics are also enhanced by IMED. Then, construct the reference signal according to the prior knowledge of the rotating machinery and input it with the output signal of IMED into the VME model together, and the output result of VME not only could further enhance the impulse characteristic of the vibration signal, but also obtain the modulation characteristic simultaneously. Finally, perform envelope spectral or enhanced envelope spectral on the output of VME and the fault features are identified successfully. Three main contributions are contained in this work: (i) An IMED method is proposed which overcomes the shortcomings of MED and other related MED improved method, and it could recover much more repetitive impulse components than the other methods; (ii) VME with constructed reference is proposed and used to extract the specific component buried in other interferences correctly; and (iii) The proposed combined method can deal with both experimental signal and engineering signal, and its advantages over the other methods are evident.

The remaining chapters of this paper are organized as follows. Section 2 and 3 presents the calculation theories of VME with constructed reference and IMED in details respectively. Flow charts of the proposed method and its application in fault diagnosis are described in Section 4. The applications of the proposed method on one experiment case and one engineering case are shown in Section 5. Conclusions are obtained in Section 6.

2. VME with constructed reference

It could be known that the decomposition result of VMD is restricted by the penalty parameter and the number of modes according to its basic algorithm and principles [16-18]. Besides, the optimal number of modes must be determined before the decomposition is started for VMD. Otherwise, when the number of setting modes is too high, certain interference patterns will appear, which affects the extraction of valid information; when the number of setting modes is too low, modal aliasing will appear. VME is the improved method originating from VMD, and the difference is that VME only extracts the target signal in contrast to VMD as mentioned earlier. It is necessary to decompose the signal into several modes by VMD firstly when using VME to analyze the signal, then use Wiener filter to filter each of the obtained modes, and a specific mode near the center frequency is extracted according to the obtained approximate value of the center frequency of the signal finally. Besides, the extracted specific mode has nothing to do with other modes decomposed by VMD. Compared with VMD, VME not only eliminates the limitation of the selection optimal number of modes, but also has a high convergence speed and reduces the computational complexity. Based on the principle of VME algorithm and its advantages over VMD, this paper proposes a new method naming VME with constructed reference, that is, a reference signal is constructed according to the prior knowledge of the diagnosis object, and then input it with the original fault signal into the VME algorithm model simultaneously to extract the target signal more effectively. Principle of the VME algorithm can be found in [19], which will not be repeated here. The basic process of the VME with constructed reference signal is described as follows through a simulation.

A simulation signal whose time-domain waveform as shown in Fig. 1 is analyzed by VME, which is composed of three components: sig1 is the simulated vibration signal of rolling element bearing, whose mathematical equation could be described by Eq. (1) [26-27]:

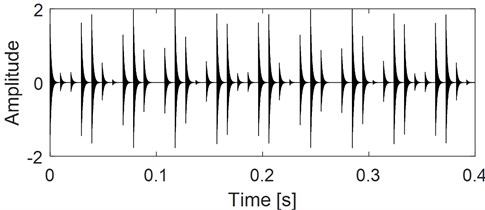
In which the inner race fault characteristic frequency (FCF) is set as $f_i$ = 102 Hz, rotating frequency is set as $f_r$ = 12 Hz, and the sampling frequency is set as $f_s$= 25600 Hz. ${\tau }_i$ represents the random slide between the rolling elements and the races, whose standard deviation is 0.5 % of the shaft rotating frequency. Sig2 is a sine signal and Sig3 is random white noise. Construct a reference signal whose time-domain waveform is shown in Fig. 2, and the characteristic frequency of the constructed signal is set same as Sig1. Then input it with the simulation signal into VME model, and the last output result is shown in Fig. 3, in which Sig2 is the extracted sine component and Sig1 is the extracted simulation signal of rolling bearing, and it could be concluded that satisfactory extraction results are obtained:

Fig. 1Simulation signal

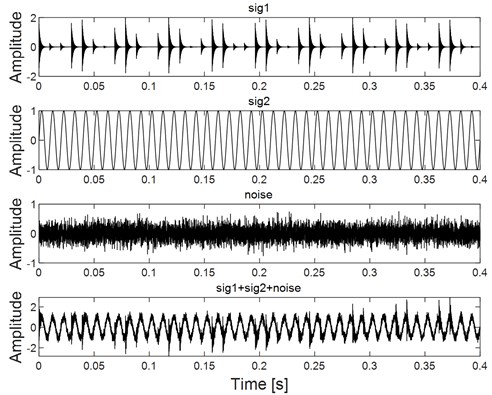
Fig. 2Constructed reference signal

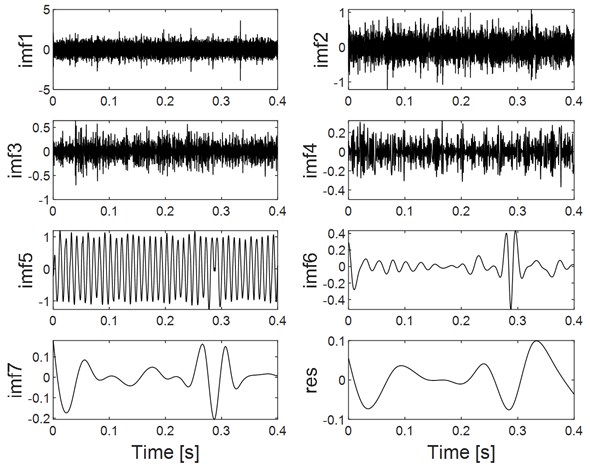
EEMD [28] is the improved method of EMD which makes full use of the influence of Gaussian white noise on the decomposition results of EMD, and it overcomes the shortcomings of mode mixing phenomenon owned by EMD. To verify the advantages of VME, apply EEMD on the same simulation signal as shown at the bottom figure of Fig. 1 and the decomposition results are given in Fig. 4, in which imf1 could be regarded as the extracted simulation signal of rolling bearing. The advantage of VME over EEMD is evident through comparing the extraction result as shown in Fig. 3 by using VME and the extraction result as shown in Fig. 4 by using EEMD.

Fig. 3Extracted results of the simulation signal by using VME

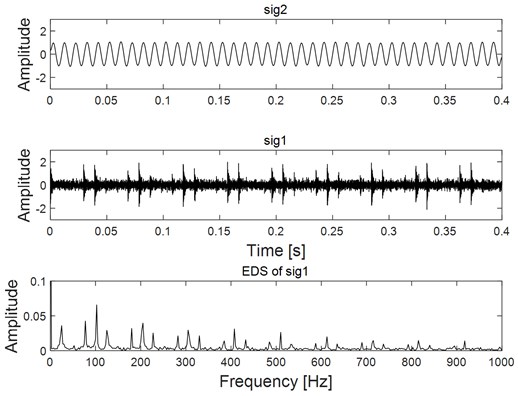
Fig. 4Decomposition results of the simulation signal by using EEMD

3. IMED

The vibration signal of faulty bearing or faulty gear will take on impulse characteristics usually, and suppose that the faulty signal is expressed by Eq. (2):

where $x$ represents the collected signal; $y$ is the original impulse characteristic signal; $e$ represents the background noise, and $h$ represents the influence of signal acquisition path on the impulse characteristic signal.

Same as the ideology of MED, the basic ideology of IMED is to construct an optimal filter in a non-iterative way to recover the original impulse characteristic signal, and the process could be expressed by Eq. (3):

where $k=\mathrm{1,2},\cdots ,N-L$.

As mentioned in the introduction, compared with the classical MED algorithm, the MCKD method optimizing the optimal filter with the maximization of the correlation kurtosis as the objective function not only could reflect the continuity of the impulse signal when failure arises in rolling bearing, but also could measure the proportion of periodic impulse sequences. However, in addition to the drawbacks described in the introduction, the noise reduction effect of MCKD is also affected by the length of the filter: if the length of the filter is too large, the amount of calculation will be increased. Besides, the period is need to be rounded or adjusted by resampling when the period is a decimal. In view of the periodic impulse characteristic of the vibration signal of faulty bearing or gear, a multi-point D-norm (Multiple D Norms, MDN) is proposed on the basis of the D-norm in the MED algorithm, that is:

The IMED algorithm uses a time target vector to define the position and weight of the impulse sequence obtained by deconvolution, and this target vector is well suitable for vibration feature extraction when a shock pulse is generated per revolution of rotating machinery. Furthermore, IMED is also applicable for non-integer fault without resampling. The target vector $t$ in Eq. (5) defines the position and weight of the impulse component of the convolution target. The effect of IMED achieves the best when the original impulse characteristic signal $y$ is completely consistent with $t$. At the same time, the MDN value in Eq. (4) reaches the maximum value, and the filter $f$ is the obtained optimal convolution filter.

Transform Eq. (5) into Eq. (6) for further solution:

where $f=f_1,f_2,f_3,\cdots ,f_L$, $t=t_1,t_2,t_3,\cdots ,t_{N-L}$.

Combine Eq. (3), (5) and (6):

where $k=\mathrm{1,2},\cdots ,N-L$.

Let $X_0=[M_1,M_2,\cdots ,M_k]$, and Eq. (7) could be simplified as following:

Following equation is obtained through further sorting:

Combine $y=X_0^{T}f$ with Eq. (9), and there is following equation obtained:

Take the special solution of Eq. (10) as a set of optimal filters, which is denoted as:

The original impulse characteristic signal$y$could be recovered by substituting the optimal filter $f$ obtained from Eq. (11) into $y=X_0^{T}f$.

The simulation signal as described in Eq. (1) is used to verify the superiority of IMED. Firstly, add random white noise into it and time-domain waveform of the noised signal is shown in Fig. 5(a). Time-domain waveforms of the impulse characteristic enhanced signals by using IMED and MCKD are presented in Fig. 5(b) and Fig. 5(c) respectively. It could be observed that the proposed IMED method not only could enhance the impulse characteristic of the vibration signal of faulty bearing effectively, but also could extract multiple shocks through comparison between Fig. 5(b) and Fig. 5(c). In addition, Fig. 5(d) and Fig. 5(e) are the relationship between the kurtosis index of the impulse enhanced signal and the iteration number of IMED and MCKD: it could be seen that the output signal of IMED with biggest kurtosis is basically obtained after about 5 iterations. However, the maximum correlation kurtosis of the impulse enhanced signal using MCKD is obtained after about 16 iterations, indicating that IMED has higher computation efficiency than MCKD.

Fig. 5Noised simulation signal handled by IMED and MCKD

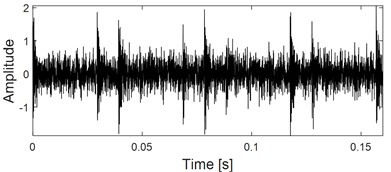
a) Noised simulation signal

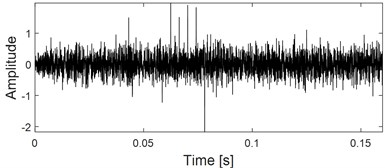
b) Repetitive impulse characteristic enhanced by IMED

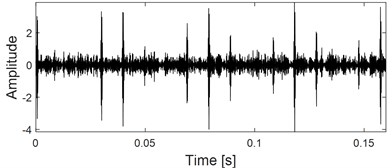
c) Impulse characteristic enhanced by MCKD

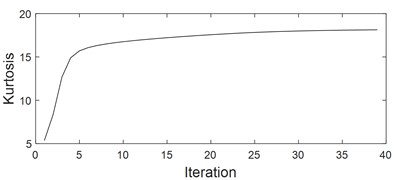
d) Kurtosis of the enhanced impulse signal by IMED with the number of iteration

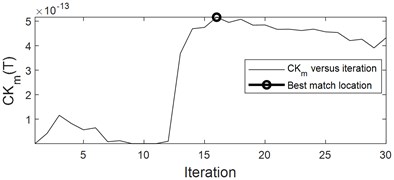
e) Kurtosis of the enhanced impulse signal by MCKD with the number of iteration

4. Flow chart of the proposed method

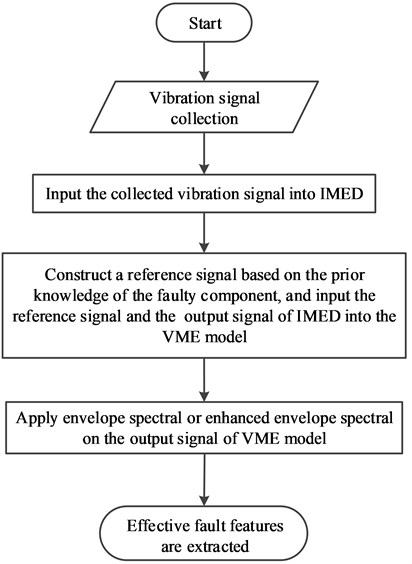
Flow chart of the proposed method to recover the repetitive impacts using VME with constructed reference enhanced by IMED is introduced in this section. This method combines both the advantages of IMED in solving the influence of the long signal acquisition path and VME based on constructed reference in extracting the impulse and modulation characteristic of vibration signal, and its specific process is given in Fig. 6 and its details are as follows:

Step 1: Install the accelerator sensor as close to the vibration source as possible to collect the vibration signal effectively.

Step 2: Input the collected signal into IMED model to minimize the influence of the signal acquisition path and enhance the impulse characteristic of fault signal preliminarily.

Step 3: Construct a reference signal with the prior knowledge of the faulty component, and the FCF of the faulty component is used as the prior knowledge in the study.

Step 4: Input the constructed reference signal with the output signal of IMED into the VME model simultaneously for better extraction result of VME.

Step 5: Apply envelope spectral on the extraction result of step 4 to extract satisfactory fault feature, and enhanced envelope spectral is another alternative if unsatisfactory extraction result is obtained by envelope spectral.

Fig. 6Flow chart of the proposed method

5. Case studies

5.1. Case 1: rolling element bearing diagnosis in laboratory

5.1.1. Data description

Effectiveness of the proposed method is verified by using the early failure data in the degradation stage of the rolling element bearing’ accelerated failure life cycle. The experiment is fundamentally different from traditional fault processing method of rolling element bearing, which is impossible to be simulated accurately using mathematical models or processing pitting methods. Details of the experiment could be referred to literature [25], and they are not presented here due to space limitations. Take one of the test bearings as research object and its relevant parameters and the calculated fault characteristic frequencies (FCFs) are presented in Table 1 and Table 2 respectively. Amplitude and kurtosis of the selected bearing over its whole life cycle are presented in Fig. 7 and Fig. 8, in which sudden change at the 2230th minute could be observed, and there is almost no change before the 2297th minute, so the collected data corresponding to the 2297th minute could be reviewed as the vibration signal of the early weak failure stage. The final disassembly diagram of the selected test bearing is given in Fig. 9, which shows that failure occurs on the inner race.

Table 1Parameters of the test bearing

Type	Ball number	Ball diameter (mm)	Pitch diameter (mm)	Contact angle	Motor speed	Load (kN)
6307	8	13.494	58.5	0	3000	12.744

Table 2Fault characteristic frequencies of the test rolling bearing

$f_r$	$f_c$	$f_b$	$f_i$	$f_o$
50	19	102	246	153

Fig. 7Amplitude over its whole life of the test bearing

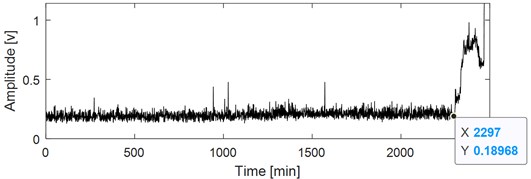
Fig. 8Kurtosis over its whole life of the test bearing

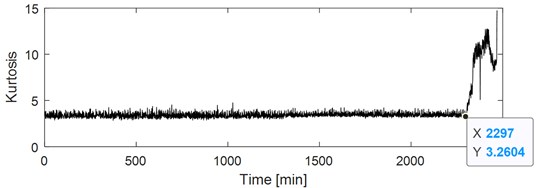
Fig. 9Fault occurring on the inner race

5.1.2. Data analysis and fault diagnosis

Time-domain waveform of the data corresponding to the 2297th minute with its envelope spectral are presented in Fig. 10(a) and Fig. 10(b): the impulse features in the time-domain are submerged completely due to the influence of strong background noise, and the energy distribution of the spectral lines locating on the inner race FCF with its harmonics are not obvious in the envelope spectral result. The original vibration signal as shown in Fig. 10(a) is firstly analyzed by IMED, and time-domain waveform and envelope spectral result of the output signal of IMED are presented in Fig. 10(c) and Fig. 10(d) respectively. It could be seen intuitively that the impact characteristics have been enhanced by comparing Fig. 10(c) with Fig. 10(a). The kurtosis values of the original signal as shown in Fig.10 (a) and the repetitive impact enhancement signal as shown in Fig. 10(c) are calculated respectively, which are 1.2 and 3.6, and this further quantifies the enhancement effect of IMED on the repetitive characteristics of the original signal. Apply envelope spectral analysis on the signal as shown in Fig. 10(c) and the corresponding result is presented in Fig. 10(d) from which the inner race FCF with its harmonics still could not be identified. Besides, misjudgment might be caused based on the analysis result as shown in Fig. 10(d), because the obvious spectral peaks could be observed roughly locating on the outer race FCF with its harmonics. The above results indicate that further processing of the output signal of IMED is needed. The reference signal is constructed based on the prior knowledge of the test bearing, that is the inner race FCF. Time-domain waveform of the constructed reference signal is shown in Fig. 10 (e). It should be noted that, the amplitude of the reference signal has little effect on the output of the VME through testing: the relationship between the amplitude of the reference signal and the accuracy of the VME’ output target signal is shown in Fig. 10(f). Subsequently, input the constructed reference signal with the signal as shown in Fig. 10(c) into the VME calculation model, and the last result is presented in Fig. 10(g): sig1 is the decomposition residual which includes the rotating frequency with its harmonics, the gear meshing components and so on, and sig2 is the target extraction component. Comparing sig2 with the signal as presented in Fig. 10(c), the impulse characteristic is further enhanced. Based on the theory of VME, the characteristic frequency of sig1 should have the same frequency as the constructed reference signal. In order to express the extraction results of the proposed method intuitively, apply envelope spectral on sig1 and the result is given at the bottom figure of Fig. 10(g), and the inner race FCF is identified ideally.

Fig. 10Feature extraction result of test bearing’ early weak fault using the proposed method

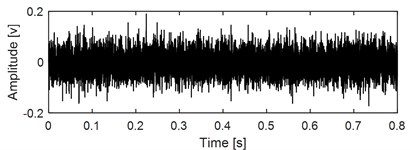
a) Time-domain waveform of the test bearing’ early weak fault

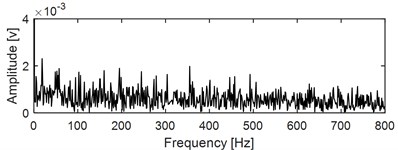
b) Envelope spectral of the signal as shown in Fig. 10(a)

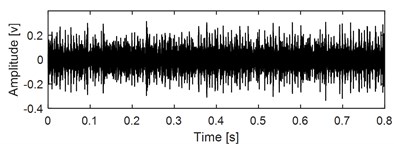
c) Repetive impulse characteristic of the signal shown in Fig.10 (a) enhanced by IMED

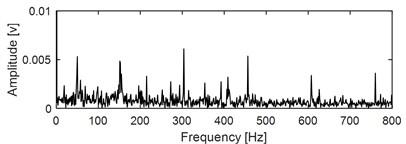
d) Envelope spectral of the signal as shown in Fig. 10(c)

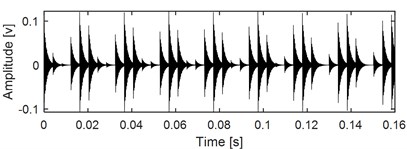
e) Constructed reference signal for the signal as shown in Fig. 10(c)

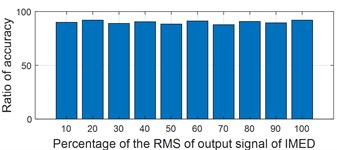
f) Relationship between the amplitude of the reference signal and the accuracy of the VME output target signal

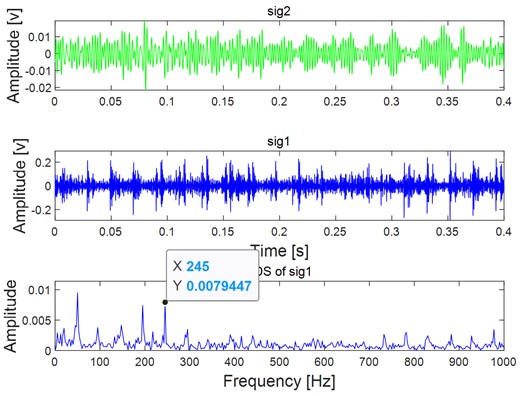
g) Extracted results of the signal shown in Fig. 10(c) by using VME

5.2. Case 2: Gear diagnosis in engineering

5.2.1. Data description

The complexity of the faulty vibration signal in engineering is much higher than that of the experimental signal, and the reasons are due to the inference of the other vibration signals of the components around the fault source and the limited condition of the vibration monitoring location. In order to further verify the effectiveness of the proposed method, it is used in gear fault diagnosis in actual engineering. The engineering research object is a coal mill in the cement plant and its structure is shown in Fig. 11. The coal mill is a machine whose function is crushing and grinding the coal into pulverized coal, and it is an important auxiliary equipment for pulverized coal stoves in the electric power and building materials industries. It will cause serious chain reaction if failure arises in it. The output speed of the motor is reduced by a three-stage gearbox, and the same gear noted in Fig. 12 is driven by the output speed of the gearbox through a coupling. The total transmission ratio of the gearbox is 5.6, and the output speeds of the motor and the gearbox are 744 r/min and 132 r/min respectively. Parameters of the open gears supported by the bearing seat are shown in Table 3. It was found that bigger vibration phenomenon occurring at both the free end and driven end of the bearing seat. The measurement points in different directions and the corresponding measurement values are shown Table 4. The sensor type is vibration accelerator, and the vibration data corresponding to the maximum vibration value that is 14.39 m/s/s (horizontal direction of the driven end the bearing seat) is selected for analysis. Since both the rotating frequency and the meshing frequency are low, the sampling frequency could be set a little lower, that is $F_s$ = 853 Hz. The length of the sampling data is set as $L$= 32768 in order to obtain high resolution.

Fig. 11Structure of coal mill

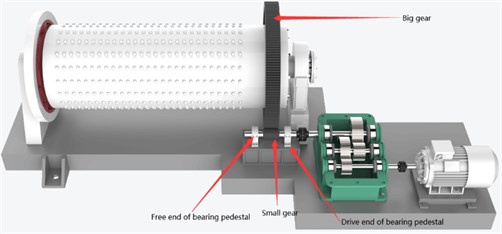
Fig. 12Fault location occurring on the small gear

Table 3Parameters of the open gears

Gear name	Tooth number	Rotating speed (Hz)	Mesh frequency (Hz)
Big gear	241	0.247 Hz	59.4
Small gear	27	2.2 Hz

Table 4Values of the measuring points

Number	Measuring points	Direction	Measuring values (m/s2)
1	Drive end of bearing pedestal	Horizontal	14.37
2		Vertical	12.29
3		Axial	8.91
4	Free end of bearing pedestal	Horizontal	10.72
5		Vertical	9.1
6		Axial	6.29

5.2.2. Data analysis and fault diagnosis

Time-domain waveform of the selected vibration signal is presented in Fig. 13(a), and Fig. 13(b) is its corresponding envelope spectral result. Theoretically, it will present an impact and modulation phenomenon in the time domain waveform, and a spectral line distribution structure with the meshing frequency as the center frequency and the mesh gear speed as the side frequency will appear in the envelope spectral. However, neither of the above features could be reflected. The root reason is that when failure occurs on the small gear, the vibration energy aroused by the failure source is very weak compared with the large gear rotating vibration energy, meshing frequency energy and gearbox output signal energy. Apply IMED on the original signal same as the experiment and the output signal is shown in Fig. 13(c), and it could be seen that both the impulse and modulation characteristics of the faulty gear signal have been enhanced. However, the fault features still could not be extracted by applying envelope spectral on the signal as shown in Fig. 13(c), which could be verified by Fig. 13(d). The output signal of IMED should be further processed according to the proposed method. Firstly, it is necessary to construct a reference signal of the faulty gear based on the prior knowledge of the faulty gear, namely the meshing frequency and the rotating frequency of meshing gear. The constructed reference signal of faulty gear could be referred to Eq. (12) and its time-domain waveform is shown in Fig. 13(e):

12

$g_r=\left[1+3\mathrm{c}\mathrm{o}\mathrm{s}\left(2\pi f_{r}t\right)\right]\mathrm{*}\mathrm{c}\mathrm{o}\mathrm{s}\left(2\pi f_{m}t\right),$

where $f_r$ = 0.247 Hz is the rotating frequency of big gear, and $f_m$= 59.4 Hz is the meshing frequency.

Input the constructed reference signal of faulty gear with the signal as shown in Fig. 13(c) into VME model simultaneously, and the extracted signal is shown in Fig. 13(f) whose impulse and modulation characteristics are further enhanced. Apply envelope spectral on the extracted signal as shown in Fig. 13(f) and the result is shown in Fig. 13(g), based on which a spectral line distribution structure with the meshing frequency 59.4Hz as the center frequency and the big gear speed 0.247 Hz as the side frequency could be observed roughly, which verifies the feasibility of the proposed method in engineering application. However, in order to reflect the extraction effect more intuitively, apply fast spectral correlation (FSC) [29] and enhanced envelope epectrum (EES) [30] on the signal as shown in Fig. 13(f). Compared with spectral correlation (SC), FSC has much higher calculation efficiency and much more outstanding capturing ability of the cyclostationary signal by refining frequency resolution arbitrarily. Besides, the performance of EES is also improved by introducing the kurtosis weighting scheme into FSC. The corresponding two-dimensional FSC image of the signal as shown in Fig. 13(f) is presented in Fig. 13(h) from which relative evident modulation phenomenon could be observed. EES of the signal as shown in Fig. 13(f) based on the obtained FSC result as shown in Fig. 13(h) is shown in Fig. 13(i), which reflects the modulation phenomenon much more intuitively.

Fig. 13Feature extraction result of engineering gear’ early weak fault using the proposed method

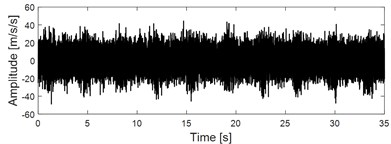
a) Time-domain waveform of the vibration signal of faulty gear

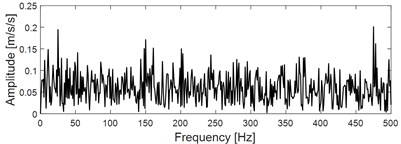
b) EDS of the vibration signal as shown in Fig. 13(a)

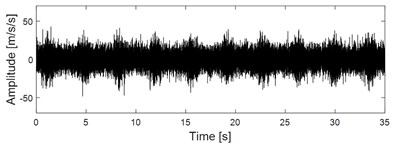
c) Repetive impulse characteristic of the signal shown in Fig.13 (a) enhanced by IMED

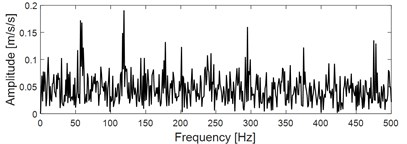
d) EDS of the vibration signal as shown in Fig.13 (c)

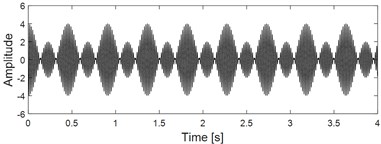
e) Constructed reference signal for the signal as shown in Fig.13 (c)

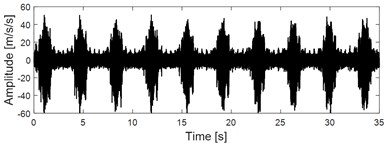
f) Extracted results of the signal shown in Fig. 13(c) by using VME

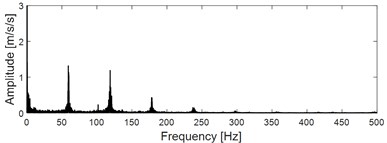
g) EDS of the vibration signal as shown in Fig. 13(e)

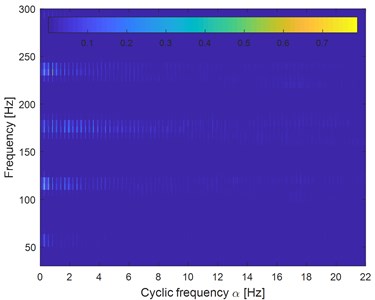
h) FSC image of the signal as shown in Fig. 13(f)

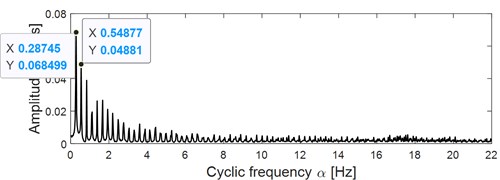
i) EES of the signal as shown in Fig. 13(f) based on the obtained FSC result as shown in Fig. 13(h)

6. Conclusions

A repetitive impulse recovering method using VME with constructed reference enhanced by IMED was proposed for fault diagnosis of rotating machinery. The proposed method uses the feature enhancement effect of IMDE on the repetitive impulse component in the vibration signal and the accurate extraction effect of the target signal based on VME with constructed reference comprehensively. One laboratory case and one engineering case analysis results demonstrate the effectiveness and advantages of the proposed method. Mainly conclusions are summarized as follows:

1) The advantages of proposed IMED in repetitive impulse characteristic enhancement effect over traditional MED method such as MCKD is highlighted through analyzing a bearing simulated signal.

2) A VME method based on constructed reference signal is proposed to improve the extraction accuracy of VME, and a simulation signal is used to verify that the proposed VME based method with constructed reference signal not only has much more precise extraction effect than the traditional VME and EEMD, but also has virtue of noise robustness.

3) The proposed fault feature enhancement method is easy to be implemented and could meet the requirements of online diagnosis, which provides a new method for fault diagnosis of rotating machinery.